《数学建模在高等数学教学中的应用案例研究》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

数学建模在高等数学教学中的应用案例研究

范文

李清华王旭

【摘要】引入数学建模是高等数学教学的有效方式.本文以返券销售系统设计为案例，通过构造消费效用函数和利润函数设计最优策略模型，利用高等数学中的积分和偏导运算解决实际问题.教学设计引入数学模型对学生理解和应用高等数学具有积极作用.

【关键词】数学建模;高等数学;效用函数;利润函数

1 引言

高等数学是现代各个学科知识的理论基础，其教学过程中无处不体现着数学建模的思维方法.极限、微积分、连续和微分方程等数学思想，以及待定系數法、最小二乘法、连续离散化等数学方法都蕴含了数学模型的建构.数学建模可以在抽象问题和实际问题之间建立联系.在高等数学的教学过程中可以通过引入数学建模的内容和思维方法分析实际问题，提升学生的数学建模意识和学习动力.本文以经济生活中的返券促销现象实施数学模型的应用教学.

2 返券系统设计

某商店采用“返券”优惠促销，当消费者消费金额满100元时，该店可赠送50元的“返券”，不足100元的部分不能获得返券.返券的用法是：每消费100元的商品，可以使用该店的50元返券，在付款时可以抵消50元，不足100元的部分忽略不计.

根据这个问题可以进行延拓，进一步考虑商家如何设计返券，从而获得最大利润.首先对符号进行说明.

2.1 消费者的消费行为

将消费者的消费行为分为两个阶段，第一个阶段是消费者第一次消费得到返券，第二个阶段是消费者使用返券进行抵扣消费.当消费者自我感觉最为划算的时候效用达到最大.消费者对若干消费品的选择，在达到每一种消费品的单位货币支付所得的边际效用相等时，实现最大总效用，即称之为效用最大化原则[1].

假设商家在没有使用返券促销活动的情况下，消费者在两个阶段均按照自己的预期消费金额进行消费，设两次预期消费金额的均值为x.当商家使用返券活动时，在第一个阶段，当消费者消费金额大于等于Y1时即可以得到价值Γ的返券，但是该返券并不能用于第一个阶段的消费，只能用于第二个阶段消费抵扣.在第二个阶段，即返券使用时期，当消费金额大于等于Y2时，消费者就可以使用返券来抵扣本次消费，如果消费小于Y则不能使用该返券.

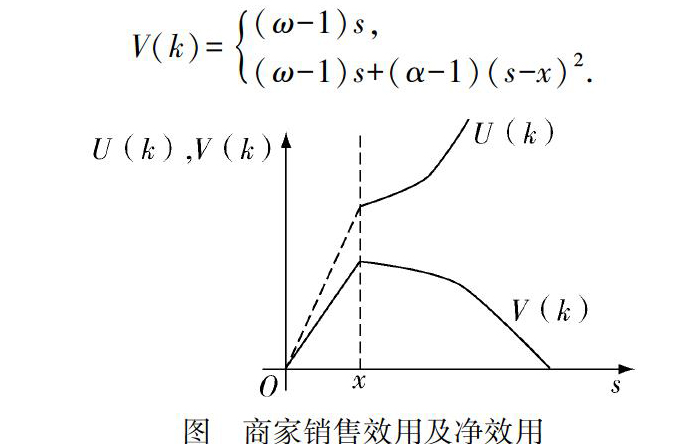
为更好地刻画消费者的行为，构建消费者消费的效用函数[2]如下：

其中x为消费者最佳的预期消费金额，s为实际的消费金额;ω是消费者实际消费金额小于等于预期消费金额时，每单位一消费金额的效用值（ω>1）;α是消费者实际消费金额大于预期消费金额时，提高单位一消费金额所得到的边际效用（0<α<1）.消费者的净效用是效用与成本之差，定义消费者消费行为中获得的净效用函数[3]为：

当返券点等于用券点时，消费者的预期消费一共有两种情况，一是预期消费金额大于等于返券点和用券点，二是预期消费金额小于返券点和用券点.当返券点不等于用券点时，比第一种情况多了一种预期消费金额介于返券点和用券点之间.因此一共有三种情况，在此一一进行讨论.

1.当消费者预期消费金额大于等于Y1和Y2时，消费者可直接获得一张返券，并且在下次消费时也不需要提高预期消费，可以直接使用返券进行抵扣消费.

2.当消费者预期消费金额同时小于Y1和Y2时，且Y1

Ⅱ.当用券点小于预期消费金额小于返券点，并且预期消费金额在Y2，Y1-r·Γ1-α时，消费者不会提高预期消费金额来获得返券.预期消费金额在Y1-r·Γ1-α，Y1时，消费者会提高预期消费金额从而得到返券，并且第二次消费仍然按照预期消费即可使用返券进行抵扣.

2.2 商家利润函数

现在考虑商家的利润，要想研究商家使用返券后的利润情况，需要同未使用返券促销的利润相比较，因此首先考虑未使用返券时商家的盈利模型.

返券促销和其他的促销方式不尽相同，返券促销的对象是在商店中消费达到一定数额的消费者.因此需考虑商店中物品的平均预付资本，即平均进价C以及平均售价P，则利润可以表示为π=P-C.利润率是剩余价值和全部的预付资本的比率，利润率是剩余价值率的转化形式.利润率可以考察商家预期利润的完成情况，也可以用于比较不同商家和不同时期的经营管理水平，从而提高经济效益[4].用A（0

当商家不使用返券促销，此时的利润模型[4]为：

2.3 商家最优策略

现在考虑商家制定返券促销的最优策略模型，在此假设返券点和用券点相同，记Y1=Y2=Y.通过商家利润函数可以得到：

3 总结

本案例建构的返券销售系统最优策略模型、消费效用函数和利润函数，有效地帮助学生理解和掌握了高等数学中的知识点，比如积分和求偏导.可见，在实际教学过程中，从问题中提炼出需要的数学知识，运用数学建模思想，构造模型的案例，不仅能够让学生感受到学以致用，也能够体现出数学的实际意义，对提高学生运用数学建模思想观察问题、分析问题、解决问题的能力具有积极作用.

【参考文献】

[1]马维娜.教育：“有价”“无价”的互构究竟是怎样的？——“泽利泽视角”的触发[J].南京师大学报（社会科学版）， 2019（5）：22-31.

[2]陈奥杰.消费者跨境电商信息偏好程度测算及其影响因素——基于跨境物流产品选择视角[D].杭州：浙江大学，2018.

[3]王炜.基于零售商返券促销的供应链运作决策与协调策略研究[D].四川：电子科技大学，2014.

[4]安欣.零售商返券促销策略与模式设计研究[D].四川：电子科技大学，2012.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。