《哈夫曼树教学探讨》-工学论文，计算机论文-论文范文参考-科学狗论文网

网站首页词典首页

标题

哈夫曼树教学探讨

范文

杜敏　郭珊珊　潘鹏　陶骏

摘要：探讨了哈夫曼树的教学要点及教学方法，以哈夫曼树的定义和意义为教学内容的开端，分步介绍了哈夫曼树的构造和运用方法，以典型的电文传输为例，剖析了哈夫曼树的要点以及编码过程的注意点。

关键词：教学设计;哈夫曼树;教学模式;问题驱动

中图分类号：G642? ? ? ? 文献标识码：A

文章编号：1009-3044（2020）02-0106-03

Abstract： This paper probes into the teaching points and teaching methods of Huffman tree. Taking the definition and significance of Huffman tree as the beginning of teaching content， it introduces the construction and application methods of Huffman tree step by step. Taking typical message transmission as an example， it analyses the main points of Huffman tree and the points for attention in coding process.

Key words： curriculum design; huffman tree; teaching model; problem driven

《数据结构与算法》课程是计算机学院学生所需要学习的一门重要必修课程。课程要求学生会把生活中大量的复杂问题简单化，对问题进行抽象建模，继而以特定的数据类型和存储结构把他们存储到计算机中去，从而可以实现某种操作。数据结构的研究范围主要涉及各种逻辑结构和物理结构，运用算法对数据进行有规则的操作。比如排序和查找，实现这些操作的具体步骤就称之为算法，算法就是对特定的数据类型进行某些操作，从而达到某种目的的过程。

《数据结构与算法》中以树形结构为非线性结构代表展开教学。树形结构是有层次的嵌套结构，它在计算机科学中具有广泛的应用，反映了数据元素之间的层次结构。本文选择了树形结构中的哈夫曼树，以课件的形式进行教学，能有效开展案例教学，实现学习过程控制的教学策略，强化学习效果。

1 教学目标

教学目标是指在教学活动中教学者所期待的所有学生反馈的学习结果，是课堂教学的出发点，教学目标始终是教学活动的过程主线。教师以教学目标为中心，制定能够引导学生学习的教学策略，学生以教师的教学目标为目标，积极展开学习。根据学生学习结果的反馈，心理学家概括出不同的学习结果，代表之一就是智力技能目标。从以上几种分类的结果可以看到一点，哈夫曼树一课中的教学目標主要为智力技能目标。那么哈夫曼树的教学目标即是学生学完本课件的内容之后，能够根据给定的条件构造哈夫曼树，并且能够写出其最短的带权路径长度。

2 学习者特征

传播学原理阐释了有效的讯息传递的条件，传播者必须了解接受者对讯息的态度、有关的知识基础和传播技能。教学活动也是一样，教学者设计的一切教学活动都是围绕学生的学习。可见，对学习者学习特征的分析是很有必要的，有效针对学习者的学习风格和学习能力，制定切合该类学习者学习特点的教学策略，从而有效阐明学习目标，达到教学效果。因此有效的教学设计必定要考虑到学习者的学习特征。学习者学习的一个重要特征就是学习的初始能力，学生学习结果的性质极大部分是由于学生对学习认知的准备状态所影响的。学习者原本储备的知识基础是自身学习新知识的重要内部条件，哈夫曼树面向的学习者在学习数据结构与算法这一课程的内容以前已经学习了C++程序设计语言及计算机导论等前导课程的内容，并且在之前就已经学习了数据结构中的树的知识。因此学生通过学习此前的教学内容以及前导课程的学习已经具备了一定的解决问题的能力和计算机程序的编写能力。

3 教学内容

观察一个例子—判定树：

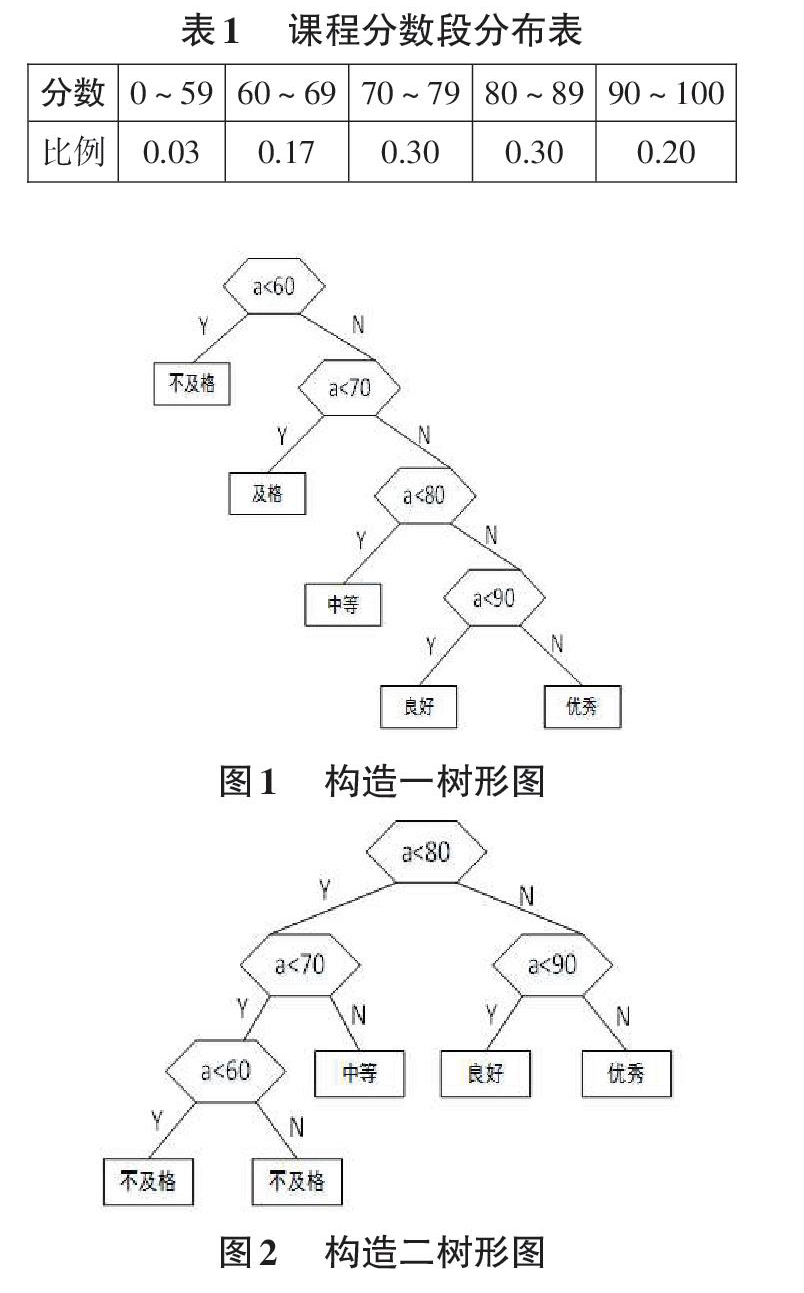
判定树指的是在处理事件的详细分析中，用树形逻辑图对单个功能与活动的一种详细分析方法。大多数问题的解决都会用到判定树，这些判断结构的设计直接影响着程序的执行效率。例如，编制一个将百分制转换成60分以下，70分以下，80分以下，90分以下，90分以上这五个等级输出的程序，用下列简单形式可以快速编写：

if（score < 60）

System.out.print（“bad”）;

else if（score <70）

System.out.print（“pass”）;

else if（score <80）

System.out.print（“general”）;

else if（score <90）

System.out.print（“good”）;

else

System.out.print（“pretty good”）;

若考虑上述程序所耗费的时间，就会发现该程序的缺陷。60分以下的情况程序只需要判断一次，而60～70分的情况程序需要判断两次，以此类推，若是分数情况较多那判断的次数岂不是更多，况且实际应用中在五个等级上所分布的学生成绩是不均匀的。当学生百分制成绩的录入量很大时，上述判定过程需要反复调用，此时程序的执行效率将成为一个严重问题。

如表1的表格就是在一次考试中数学课程的各分数段的分布情况：

现按照表格条件利用哈夫曼树来寻找一颗最佳判定树，即总的比较次数最少的判定树。

第一种构造方式：

第二种构造方式：

显然后者的判定效率要比前者高。

所以称判定过程最优的二叉树为最优二叉树，即哈夫曼树。

3.1 概念

路径：树中一个结点到达其子孙所经过的结点集合。

路径长度：在树的一条路径中，每走过一个结点路径长度都要加一。

权值：每个树结点所在的数值，通常指字符对应的二进制编码出现的概率。

结点的带权路径长度：指的是在一棵树中，结点到树根之间的路径长度与该结点上权的乘积。

3.2 哈夫曼树的构造

哈夫曼树被定义为一种带权路径长度最短的树。要使得二叉树的WPL值最小，那么该二叉树的根结点以下的叶子结点为所有权值中较大的值，而所有权值中较小的值都會远离该二叉树的根结点。哈夫曼善于总结，他根据这一特点，提出了一种构造最优二叉树的方法——哈夫曼算法：

给定n个数值为权值，要求构造一棵最优二叉树即哈夫曼树。给出哈夫曼树的构造规则：

（1）在给定的n个权值中选出两个最小的值，让它们构成一棵新的二叉树，新二叉树的左右叶子结点的值就是它们的值，新树的根结点的权值就是这两个叶子结点权值的和;

（2）在原来给定的所有n个权值中删除上一步已用的两个最小权值，并将新二叉树的权值加入n-2个权值中去;

（3）重复上面两个步骤，当所有权值都出现在这一棵二叉树上时，这棵树就是所需要构造的哈夫曼树。

这里要注意几点：

（1）哈夫曼树不唯一;

（2）哈夫曼树的子树也是哈夫曼树;

（3）哈夫曼树中无度为1的结点;

（4）有n个叶子结点的哈夫曼树，其总结点数为2n-1。

在处理问题时，我们设立的目标不同，解决问题的过程中使用的方法也就有所不同。但是解决方法一定是要符合处理条件的。比如上述的二叉树，要使得构造的树带权路径长度最小，那么它所涉及的处理方法可能要求达到某种空间资源的最小化，或者时间的最小化，于是哈夫曼树在理论上便有了应用价值。

3.3 哈夫曼树在编码中的应用

用于通信编码：

在电报通讯中，电文是需要在字符和二进制编码之间相互转换从而进行传送的，电文以二进制的0，1序列传送。在发送端需要将电文中的字符序列转换成二进制的0，1序列，而在接收端又需要把接收的0，1序列转换成对应的字符序列。

例如给出的这段电文：WRGPWPRGGRPPGPWRGP

电文中使用了W，P，G，R这四种字符，每个字符出现的频率分别对应3，6，5，4，将它们进行二进制等长编码，则编码依次为W：00? P：01R：10? G：11

所发电文为：

00101101 00011011 111001 0111 01? ?00101101

采用不等长编码容易产生二义性或者多义性。这里有一个例子，A：010，B：0101，C：001，D：1010字符A的编码010与字符B的编码0101的前一部分重合。在这种情况下，0101010，同样表示了BBA的代码和AD的代码，这种情况的编码就产生了译码的二义性。

所以，采用不等长编码容易出现二义性。为了解决这个问题，可以将字符集里的每个字符赋予叶子结点的含义，这样就能生成一颗编码二叉树，使该字符结点的权值表示的是字符出现频率的含义，有了这些条件之后便能求出树的最小带权路劲长度，其表示的含义就是传送电文的最短长度。这里就存在以频率赋予权值所出现的哈夫曼树的问题。

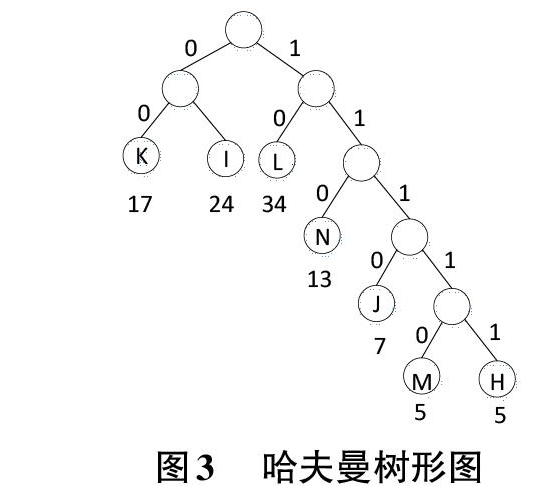
比如此处存在7个字符{H，I，J，K，L，M，N}，这7个字符的出现频率为{5，24，7，17，34，5，13}，若将它们存入至文件中去，可使用哈夫曼树构造不等长编码进行存储，并且符合前缀编码的要求。

H：111? I：01 J：111K：00 L：0M：11 N：11构造树形如图3所示：

哈夫曼树构造完成以后，须从叶子结点出发走到根部从而求出编码。

构造过程总结：

（1）对两个最小者的选择为双亲下标为0的结点;

（2）对选出的两个最小者，修改双亲下标为新结点的下标;

（3）新结点的左右孩子修改为所选的两个新结点的下标;

（4）新结点的权值为两个结点权值之和。

最后给出哈夫曼编码的简要算法：

//结点的结构体类型

public class HTNode

{public int weight;? //结点的权值

public int parent;? //结点的双亲

public intlchild;? ?//结点左孩子的下标

public intrchild;? //结点右孩子的下标

};

voidCreateHuffmanTree（ListHT，int n）

{

if（n<=1）return;

m=2*n-1;

HT=new HTNode[m+1];

//0单元未使用，此处需要动态分配m+1个单元，HT[m]为根结点

for（i=1;i<=m;i++）

//将1～m的结点双亲，左右孩子的下标都初始化为0

{

HT[i].parent=0;

HT[I].lchild=0;

HT[i].rchild=0;

//输入n个叶结点的权值

for（i=1;i<=n;i++）

{

System.out.print（HT[i].weight）;

}}}

4 教学策略

教学设计是一个系统过程。在哈夫曼树教学设计中有如下的教学策略。

概念的教学策略。该教学设计中必须讲解的概念有：路径、路径长度、树的路径长度、带权的路径长度、树的带权的路径长度、空心二叉树和哈夫曼树等。该教学设计中的概念的讲解使用如下的组织方式。讲解概念所用方法：使用文本直接呈现哈夫曼树所涉及的知识概念。使用动画图表演示概念的简单实例。介绍完概念后，普及哈夫曼树在编码中的实际应用，用以锻炼学习者的思考能力，进而保持对哈夫曼树知识的注意。给出相关概念的练习题，类型为填空题以及选择题。给出进阶应用编程题，用以锻炼学习者的思维能力以及编程能力。

规则的教学策略。该教学设计的规则为哈夫曼树的构造算法。采用的教学方法是规则—实例的方法。为了使学生能有效地学习哈夫曼树知识，采用图形与文本相结合的方式，交错传递哈夫曼树的知识概念及应用。即先以文本的形式呈现哈夫曼树的构造算法，接着再以图形动画演示用构造算法构造哈夫曼树及求哈夫曼树的带权路径长度的过程。讲解完后提供习题小测验，类型为填空题以及选择题。学生回答问题之后，教学者对学生的答案进行检查，如果学生的答题情况很差即没有答对所列题目中的百分之八十，下次课程则应继续巩固基础概念，调整学习进度从而达到教学效果。

5 总结

完整的教学设计应包含教学目标、学习者特征的分析以及教学内容形式的确定。学生是教学活动的关键，教学设计应围绕学生的理解能力来开展。对于哈夫曼树教学设计来说，它所涉及的思维传达方式尤其重要。因哈夫曼树一课中的学习内容多且知识点间的关系复杂，所以要将这种抽象的逻辑理念表示成超文本的形式是非常困难的，但是在教学设计中编排图片、动画极大优化了学习效果。

参考文献：

[1] 火旺.数据结构与算法[M].西安：西安电子科技大学出版社，2005：125-127.

[2] 克抗.计算机辅助教育[M].北京：高等教育出版社，1997.

[3] 齐超.哈夫曼编码及其应用[J].郑州市电子信息工程学校学报，2014，12（1）：256.

[4] 太山，郭观七，李文彬.课堂设问的技巧及其在《数据结构》课程教学中的应用[J].湖南理工學院学报：自然科学版，2015（1）：81-83.

[5] 哈夫曼算法在分类优化应用中方的缺陷及修正[J]东华大学计算机科学与技术学院学报，2010，9（7）：60-62.

[6] 孟凡荣，贾杰，王兴伟.网络工程专业创新性实践课程体系构建与实施[J].计算机教育，2013（14）：104-108.

[7] 逯鹏，张赞.数据结构课程教学方法的研究和实践[J].教育教学论坛，2015（18）：121-123.

[8] 莹.哈夫曼树遍历算法的优化[J].安徽电子信息技术学院学报，2009，25（5）：7235.

【通联编辑：王力】

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。