网站首页  词典首页

请输入您要查询的论文：

　

标题 高中数学核心概念及其教学策略探究
范文 雷蕾


[摘 要] 数学概念是数学学科课程内容的基本组成要素，处于学科的中心位置，对于学生学习数学知识具有重要的支撑作用. 本文在分析数学核心概念的内涵和特征的基础上，提出了一些高中数学核心概念教学策略.
[关键词] 高中数学；核心概念；内涵；策略
随着近几年数学改革越来越多元化，高中数学概念教学越来越被重视，尤其是处于连接知识与知识，构成知识体系的核心概念教学更是受到极大的重视. 高中课程新标准在解读“核心概念”时也明确指出要重视“核心概念”产生数学思想，学习数学概念是数学基础. 因此数学教学中教师应以核心概念的构建为突破口，引领学生更加深入地领悟概念，引发心理共鸣，形成内心感悟，从而真正优化学生的认知结构.
[?] 数学核心概念的内涵解读
数学概念是用高度概括化语言描述研究对象空间和数量关系，具有“内涵和外延”双重性，所以数学概念具有稳定性和灵活性.
高中数学核心概念就是指高中数学学科的主干知识，能够形成数学这门学科的所有概念和所有原理的知识. 高中数学概念就是高中数学知识的核心，如函数概念、统计概念以及导数概念等，始终作为高中数学概念的核心贯穿教材始终，并将主导高中数学的思想形式（如数形结合思想、空间思想、统计学思想等）. 但是还有学者认为，核心概念就是一种即使忘掉其基础信息或者次要信息，但依旧能被广泛应用的陈述性知识. 又或者将那些早已经超越高中数学教学的，并且会随着时间变化而不会改变价值的概念叫作核心概念.
[?] 高中数学核心概念的特征
1. 高中数学核心概念具有基础性
核心概念将数学思想贯穿整个数学知识体系，这对于整个数学学科的发展都具有基础性. 其余概念也是因它而生，所以体现其核心性. 例如，函数概念不仅可以延伸出奇偶性，还有周期性、单调性，一次函数、二次函数、指数函数、对数函数等，这些概念的基础都是“函数”概念，所以很好地体现出了核心概念的基础性.
2. 高中数学核心概念要具有联系性
高中数学核心概念就是能将普通的一般概念联系在一起的“组织者”，这也体现了核心概念与概念的关系. 例如，在三角函数中，“三角函数”概念就是核心概念，以它为基础，能够推出单调性、函数图形、弧度制、三角函数性质、三角函数应用、诱导公式等一切基础概念，这就是起到核心概念的“联系性”.
3. 高中数学核心概念具有丰富性
通过对核心概念的描述得知，核心概念是非常丰富的概念，其包含的内容非常多，这不是一个简单的概念所能比拟的，其作为一个基础概念，自然会涉及多个下位概念，其所体现的数学思想也是无穷无尽的，异常丰富，甚至还存在于其他学科交叉的现象，所以其丰富性很强. 例如，对于一个以原点为中心，2为半径的圆，通过“集合”概念，可以表示为P={（x，y）∈R
x2+y2=4}，这就体现出集合的丰富性，准确用P={x
p（x）}来表达所以具备P性质的点，这让整个概括更加整齐，更具有研究的价值.
[?] 高中数学核心概念教学策略分析
通过对高中核心概念的分析和认识，加强教师对核心概念的理解和教学，做好学生对核心概念问题的掌握，扩大学生的思维方式.
1. 对于核心概念要加强理解推导过程
在核心概念的推导过程中学生往往会出现理解不透彻的现象，并且很容易将核心概念与一般概念弄混淆，所以在核心概念教学策略中，首先要指导学生对核心概念的理解和认识，注重其推导过程，这才是核心概念被学生掌握和利用的基本要求. 例如，在“三角函数”核心概念中，要掌握其两角和差公式，但是这套公式本身比较复杂，而且推导过程也比较麻烦，所以很容易造成学生在研究和使用中不注重对其推导过程加以理解，只会“死记硬背”，经常出现错误. 教师需要帮助学生演示该过程的推算规律和三角函数的运算法则，在对二倍角和和差公式的推算中加强学生对于核心概念的理解和产生思维方法，并促进计算. 例如，在“sin145°sin205°+ sin245°sin335°”的解答过程中需要对两组计算进行变形，通过正余弦变化、和差公式的推导、余弦公式，最终结合诱导公式导出结果. 这道例题就充分展示了对核心公式的推导与演示，让学生在正余弦公式、两角和差公式的演示推算中理解和把握核心概念的推導，进一步解决问题.
2. 充分利用概念二重性的性质
高中数学核心概念也是要遵守概念的二重性，即概念既可以是整个过程，也可以是被认知的对象，所以可以借助二重性来解决核心概念的教学.
（1）通过过程化的概念，解决概念的认知
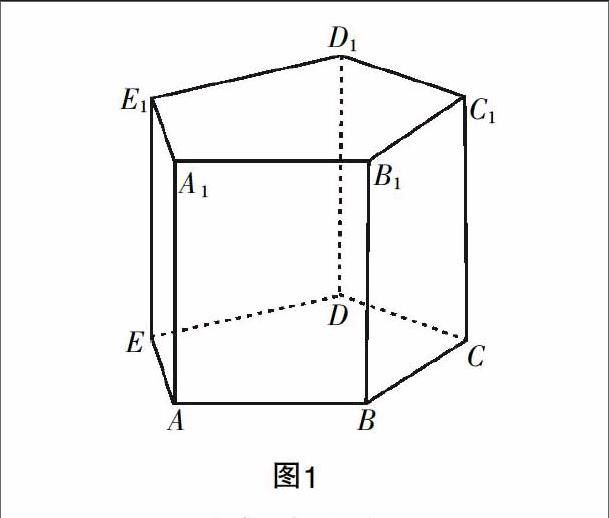
由于核心概念在认识上比较抽象，于是在认知过程中可以先通过过程来理解核心概念，然后再将其放置在被研究的对象上，增加学生理解的过程，不只是记住概念，而且还要形成良好的思维方式. 例如，在“立体几何”核心概念的理解中，学生先通过对“立体几何”的描述来理解概念，但是可能还是不完善，于是教师可以借助多媒体将“立体几何”图像投影在黑板上，学生自然在研究过程中就掌握了“立体几何”的概念，弥补描述的不足. 再如，在几何图形的“棱柱”概念的教学中，可能学生对“棱柱”概念认知不熟悉，但是可以借助“棱柱”的几何图形解释的过程来解释不同的“棱柱”概念. 学生先将“棱柱”的概念从字面上进行理解，看看能理解到什么程度，紧接着教师将图1投射到幕布上，学生看见图形，再结合棱柱的概念，然后通过添加不同的条件，如添加“棱AA1垂直于底面ABCDE”，那么这个棱柱就变成了“直棱柱”；又或者加上“底面ABCDE是正多边形”，那么通过过程变化，形成了“正棱柱”的概念. 所以正是不同的过程变化，导致出现不同的“棱柱”的概念，帮助学生熟练掌握.
（2）反思进步，实践验证
在核心概念教学中要善于反思，总结学生认识的不足，并组织学生进行实践验证. 例如，在学习“空间点线面”后，要结合生活，观察概念学习是否准确，利用教室中的桌椅板凳来实践，通过其位置进一步认识核心概念的定义.
学生对于核心概念的理解不是一朝一夕的，而是需要反复渐进，并长期坚持，最终才能加深理解，所以教师要在这个过程中不断重复核心概念，利于学生记忆.
3. 概念非形式化的合理使用
如果学生能够通过自己的描述准确反映核心概念的内容，那么会对概念的教学大有裨益. 在教学概念之前，可以组织学生先通过自己探索将核心概念用非形式化的语言表达出来，然后教师再组织学生验证和修改核心概念的“描述”. 例如，在“一元二次函数”概念教学中，教师通过对“一元一次方程”和“一元一次函数”解读，指导学生对比“一元二次方程”与“一元二次函数”，学生自己探索认知的概念最牢靠，也便于学生打开思维，提升解决问题的能力.
4. 充分应用，全面掌握核心概念
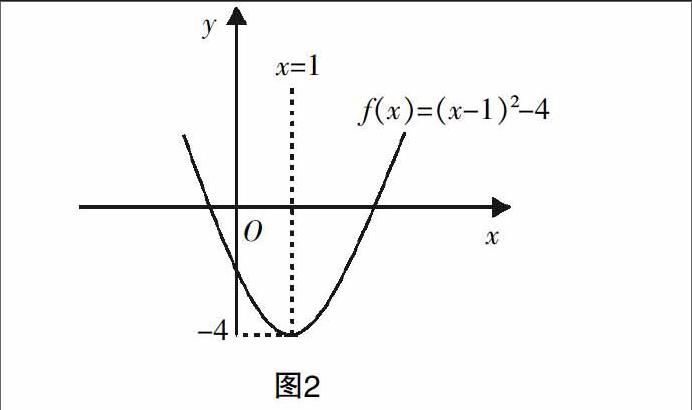
对于高中数学核心概念的应用是掌握核心概念的关键，概念在认知中会经历“模糊—具体”的变化，而教学过程是“模糊”过程，但是应用概念的过程却是比较清晰的过程，所以高中数学教师要加强学生对数学概念的应用，然后进一步深刻地理解和把握核心概念. 例如，在二次函数概念讲解完毕后，教师可以运用函数例题来检验学生的掌握情况：求f（x）=x2-2x-3在区间[2，a-3]上的最小值. 这道题要根据二次函数的概念，并结合参数讨论求解. f（x）=x2-2x-3=（x-1）2-4，根据二次函数的概念画出函数曲线（如图2）.
当x=1时， f（x）可以取得最小值-4，那么依据二次函数的概念，可以对a-3进行参数讨论，最终确定在区间[2，a-3]上求函数的最值问题. 本题就是通过对二次函数概念的灵活运用，展示学生对概念的理解能力和水平，从而让学生更好地掌握数学的核心概念.
总之，数学概念是数学学科课程内容的基本组成要素，对于学生学习数学知识具有重要的支撑作用. 掌握核心概念，也是高中学生学好数学的关键. 因此，在高中数学概念教学中，教师应以核心概念的构建为突破口，用科学的方法研究核心概念理论，并指导核心概念教学实践，使学生在亲历构建概念、运用概念的过程中，实现对概念的透彻理解，主动地进行知识建构和意义学习.
随便看

　

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。

　

Copyright © 2004-2023 puapp.net All Rights Reserved
更新时间：2024/12/23 3:47:17