[摘 要] 解析几何是中学数学的重点和难点，学生在学习解析几何中遇到学习困难的因素是多方面的，引导学生解决解析几何学习中的困难，是提高其圆锥曲线问题解决能力的关键.
[关键词] 解析几何；数学；困难；因素；对策；双曲线；概念；性质
解析几何是高中数学知识体系中非常重要的一块内容，是提高学生的数形结合能力、运算求解能力、数据处理能力的重要载体之一. 在教学的过程中，通过不同曲线的教学，让学生能从直观入手，归纳总结出不同曲线的几何性质，并能用通过代数运算或结合几何性质来解决相应的解析几何问题. 但是在学生学习解析几何的过程中存在着很多困难，教师也在不断地改进解析几何的教学过程，如何提高学生学习有效性，如何提高教师教学有效性，是值得深入研究的.
一方面是学生的学习过程中，学生感觉解决解析几何问题时的方法选择上比较单一、模式化，计算错误频现，做题积极性不高；另一方面教师在教学的过程中，如何才能找到学生的“最近发展区”，让学生在已有的知识和能力的基础上，更好地体会和探究解析几何问题解决的一般解题规律，探寻解析几何的本质，这也是教师需要思考的问题.
[?] 问题的归因与分析
造成学生解析几何学习困难的成因是多方面的，主观方面有学生学习的方法、思维以及心理等原因，客观方面有教师在教学中存在的一些问题.原因分析如下：
1. 初中平面几何教学与高中解析几何教学的衔接不协调
学生在初中阶段学习平面几何的时候，一方面对于刚刚接触几何的初中来说，几何方面的知识储备是非常少的，另一方面学生的生理成长阶段决定了他们还没有达到一个很高的抽象概括和逻辑思维能力水平，也认识不到抽象出来的概念之间存在的内在关系，而推理是建立在对概念的理解上的，因此很多学生并不适应严密的推理过程和形式.尤其是初中新课程实施以来对平面几何教学要求的降低，“三段论”推理教学没有很好落实. 使得学生往往重于结果，轻推理过程.学生平面几何知识的匮乏，逻辑能力不高，导致解析几何学习困难加大.
2. 解析几何概念性质存在理解困难
直线中倾斜角与斜率的相关概念联系，直线和圆、两圆位置关系，椭圆、双曲线、抛物线的第一定义、性质等等对于学生而言難度较大，其内容本身比较困难，形式化程度较高，对于学生的理解存在障碍.
3. 学生运算能力的不足以及对于运算存在的心理障碍
计算器在初中教学中的应用，降低了对学生运算能力的要求，导致学生对基本的数字运算普遍能力不高. 初中数学对字母运算和因式分解教学要求降低，导致学生在解析几何学习时对于字母运算和变形化简显得力不从心. 即使是解决的方法已经找到，还是不能将问题的解决进行到底. 一方面在运算的过程频频出错，到处碰壁；另一方面是学生对于比较烦琐的数学运算存在心理障碍，或不愿意算下去，或对运算失去了信心，主动放弃.
4. 教师在教学过程中存在的一些问题
一方面教师在教学过程中偏重解题策略的寻找，轻视学生计算方法的引导，将许多计算步骤跳过，美其名曰让学生自己去算，其实学生根本没算，问题不断积累；另一方面在课堂教学中留给学生思考、交流的时间不够.再加之一种“问题模式化”的教学方式，影响了学生学习能力的提高.
[?] 案例剖析与对策
1. 概念教学
圆锥曲线的概念有很多种定义，中学数学中一般有三种. 第一种是教材中的第一定义，第二种是传统教材中的统一第二定义，第三种是教材章头图中的介绍.从教学来看，一般教学仅围绕第一定义做出了概念的阐述、分析，导致学生对椭圆、双曲线、抛物线的认知不足，现阶段不少问题并不仅仅研究与定义相关的问题，更多的是从数学本质的角度思考问题，因此要全方位地渗透定义教学是概念教学的关键. 笔者给出概念全面性的三个层次问题，提升概念学习的理解，从而解决概念学习的困难.
问题1：已知双曲线-=1（a>0，b>0），右支上一点P（m，n）到左焦点F1和右焦点F2的距离差为12，两焦点之间的距离为20，求双曲线标准方程.
问题2：已知平面内动点P（x，y）到定点A（3，0）的距离比上到定直线x=的距离值等于3，求动点P（x，y）的轨迹方程，并说明其是什么曲线.
问题3：AB与平面α所成角为20°，记斜足为B，若点C是位于平面α上的动点，且∠CAB=30°，则点C在平面α上的轨迹是______________.
分析1：从问题1可以发现，本题是典型的双曲线概念的理解和运用，学生通过第一定义可以清晰地认识双曲线的实轴和焦距，这种概念相关的问题属于第一层次，学生对于概念的理解比较到位，这是源于课堂教学中数学实验“拉链运动”环节进行的设计，从而获得了良好的解题体验.
分析2：问题2是对于第二定义的一种考查，若没有第二定义的理解和思考，本题的入手角度自然是以轨迹求解中的直接法，但是其运算量比较大，学生若能从第二定义的角度入手思考，本题的解决具备了更高的理论高度，自然水到渠成.
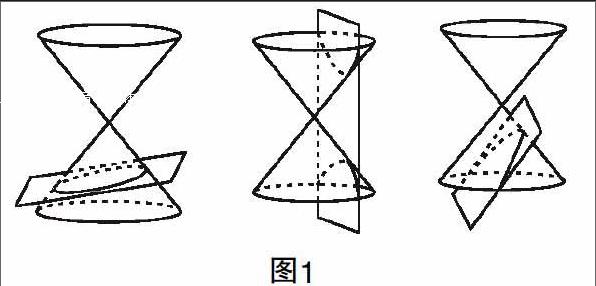
分析3：问题3是概念教学考查的核心. 从圆锥曲线名称来说，椭圆、双曲线和抛物线都是有其来源的. 古希腊数学家研究圆锥时，用不同角度的平面去截取圆锥，从而得到了不同的曲线形态. 如图，章头图很好地阐述了这种变化，教师在教学中要紧紧地以教材为主，加深概念的思辨性，从而获得概念教学的最高层次和境界.
问题的解决也比较容易，以AB轴，点C在空间的轨迹恰为圆锥的表面，现截面与轴成20°角，其小于圆锥轴与母线的夹角30°，因此显然截口曲线是双曲线.
从上述三个概念问题辨析，对于概念教学获得了层层递进式的理解和运用，让学生在圆锥曲线概念上的理解得到了进一步的提升，只要对比进行问题设计与尝试，学生获得了全面的概念感知，对于圆锥曲线概念的学习不再是难点，上述以双曲线为例，椭圆等概念读者类似可进行设计教学.
2. 性质教学
圆锥曲线的性质比较多，多数围绕对称性、离心率、位置关系等进行问题的设计. 从学生学习圆锥曲线的性质教学来看，学生对于基本性质的认识是了解的，但是并没有理解到内心深处. 作为教师知道，诸如对称性等是椭圆、双曲线等图形的基本性质，离心率是圆锥曲线统一的性质. 如何破解有关性质的难题，需要教师合理设计问题，让学生通过问题的解决获得性质使用的感悟.
问题5：双曲线虚轴的一个端点为M，两个焦点为F1，F2，∠F1MF2=120°，则双曲线的离心率为______.
分析：离心率研究是双曲线的重要性质的学习，关于离心离的解决主要是从三个方面入手的. 其一是圆锥曲线定义的使用，其二是平面几何相关性质的使用，最后是利用点坐标方式进行运算. 学生最主要的困扰在于后两种，既无视平面几何中诸如三角形正弦定理、余弦定理、角平分线性质等使用的不足，又没有从运算的角度进行足够的计算，导致离心率问题陷入困境. 思考本题不难发现，可以从平面几何图形三角形入手，结合余弦定理进行求解，给出简要解答：
总之解析几何教学是不折不扣的一个难点，但是从深入概念本质、体会性质的角度做一番独到的思辨，有助于教师在后续教学中增加教学的经验，将圆锥曲线教学化繁为易，让学生获得更多的解题体验、快乐. 限于篇幅未能就运算方面做出一进步的分析，恳请读者继续补充.
- 高考真题中熟悉而又陌生的“词块”
- 2019年高考英语全国Ⅰ卷的用词对词汇复习的启示
- 优化高考数学运算的策略
- 提升直观想象能力，培育数学核心素养
- 透视高考中“函数零点”问题
- 一类数列通项的解法探究
- 用朴素思想巧解压轴小题
- 2019年高考全国Ⅱ卷作文试题分析
- 析高考真题，探备考方向
- 针对现实，有的放矢
- 语言文字运用分析及复习策略
- 锤炼利刃巧断句
- 重视教材，强化基础，提升能力
- 基于项目研修共同体的教师专业发展模式实践研究
- 修心成海，春暖花开
- 英语书面表达的提分策略
- 以“本”为本夯基础，以“法”为辅巧做题
- 2019年高考理综生物试题分析及2020年备考建议
- 高考化学实验题的评析及复习备考建议
- 化学高考热点题型
- 凸显思维 守正出新
- 高考中有机同分异构体的计数与书写大突破
- 2019年高考理综新课标Ⅰ卷物理第21题的解析与启示
- 2019年全国Ⅰ卷物理实验题剖析及备考策略
- 例谈地理思维过程在高考中的体现及启示
- chapels
- chaperon
- chaperonage
- chaperonages
- chaperone
- chaperoned
- chaperones
- chaperone²
- chaperone¹
- chaperoning
- chaperons
- chaplain
- chaplaincies
- chaplainries
- chaplainry
- chaplains
- chaplainship
- chaplainships
- chapless
- chapped
- chapping
- chaps
- chap's
- chapter
- chapter 11
- 为计谋获得成功而得意自负
- 为讨人喜欢或哄骗人而说的好听的话
- 为讨好别人而细心伺候、奉承
- 为讨好而笑
- 为讨好而赞扬
- 为证实而核对
- 为证明某事而发誓
- 为诈
- 为诗一辩
- 为诗词谱曲
- 为诗集作的笺注
- 为诬陷人而虚构的案件
- 为请客送礼、资助、捐献等而破费钱
- 为谁辛苦为谁甜
- 为谅
- 为谋于未然，聪者或莫听；患至而后图，智者有不能
- 为谋求私利耍手段，做违法乱纪的事情
- 为谋求达到某一目的而奔忙
- 为负债牵累
- 为财而死
- 为贫乞讨
- 为贫穷牵累
- 为赌胜负而抓取的东西
- 为赏月而筑的台
- 为赴死或将死的人举行祭礼