《改进K-means算法在风电异常数据的识别研究》-工学论文，计算机论文-论文范文参考-科学狗论文网

标题

改进K-means算法在风电异常数据的识别研究

范文

李亚玲李涛

摘? 要：风电场运营管理需要对测风塔覆冰、信息传输故障、人为弃风等异常数据进行有效识别清洗，以训练风速与功率预报模型。针对利用聚类K-means算法识别这些异常数据时，无法依靠经验值事先确定 K-Means算法的聚类个数的问题进行改进。改进算法要求首先给出一个聚类个数k值的范围，然后依据数据簇类间相异度函数进行初步计算，从中获得一个最小值作为最优k值，以此来降低聚类个数确定的难度。该改进k-means算法通过某风电场的实测数据进行了验证。

关键词： K-means; 异常数据; 识别清洗; 聚类; 簇个数

中图分类号：TP311? ? ? ? ? 文献标识码：A? ? 文章编号：1006-8228（2020）02-06-03

Application of improved K-means algorithm in recognition of wind power abnormal data

Li Yaling1，2， Li Tao1

（1.Meteorological Bureau of Sichuan Province， Chengdu， Sichuan 610072， China;

2.Laboratory of Meteorological Information Sharing and Data Mining）

Abstract： In order to train the wind speed and power forecast model，the wind farm operation management needs to effectively recognize and clean the abnormal data such as the icing of wind tower， information transmission failure， artificial wind abandonment and so on. Aiming at the problem that in recognition of wind power abnormal data by K-means algorithm， the clustering number of K-means algorithm cannot be determined by empirical value， the improved K-means algorithm can first determine an optimized clustering number range for k， and then select a more optimal k value according to the preliminary calculation of the dissimilarity function between data clusters， thus reducing the difficulty of determining k value. The improved K-means algorithm is verified by the measured data of a wind farm.

Key words： K-means; abnormal data; recognition and clean; clustering; number of clusters

0 引言

风能是重要的清洁能源之一，发展风力发电对于调整能源结构、生态环境建设等有着举足轻重的作用。中国风电装机容量统计报告显示[1]：截止2018年年底，全中国风电累计并网装机容量达1.84亿万kW，连续九年位居全球第一。随着风电场规模的不断扩大，风电场及风电机组的历史运行数据的剖析对风电场运行、电力调度等都有着十分重要的意义。

本文着重研究风电机组以及风电场中测风塔的同步风速和风电功率的历史数据中异常数据的辨识。影响风速和功率数据质量因素很多[2]：电磁干扰、信息处理错误、人为弃风等均会造成大量的异常数据。这些异常数据在对于风速与功率预测模型训练中，严重破坏了风速的功率所应该有的分布规律与对应关系[3-4]。因此如何将风速与功率的历史数据进行清洗，进行异常数据辨识越来越受到关注。数据挖掘能从大量的数据中自动发现规律，它是一门新兴的综合性交叉学科。它帮助风电企业将将数据挖掘中的模型应用在风电场及风电运行机组中帮助企业管理发现知识来达到辨识风电异常数据的目的。根据风速与功率的数据特点，我们选取了聚类挖掘中的K-means算法。

1 相关技术简单介绍

1.1 K-means算法简介

对于一组需要聚类的数据元，通常来讲，基于划分的聚类需要用户事先确定想要聚类的个数K，通过反复重定位技术进行迭代，尝试通过对象在组间的移动来进行改进划分，将数据分为[c1，c2，c3，c4，…，ck]其中[k?n]。对于这些划分的结果，要求每个对象必须归属于一个划分的集合;每个划分也必须有一个对象。一个好的划分能达到同类之间的相似度较高，而不同类的对象之间的相异度比较高。

K-means算法是基于划分的一种经典聚类算法，它的核心思想是用两个数据元之间的距离来确定是否是一个簇，我们认为，这个数据元与质心距离越小，他们就相似度就越大，相异度就越小，这两个数据元就属于一个簇[5]。它主要是通過在确定初始要将对象分为簇的个数的k，然后将n个对象分为k个簇，以获得最好的一个划分。聚类完成后，所有的数据都只属于一个簇，且只聚类到离自己距离最小的簇[6]。

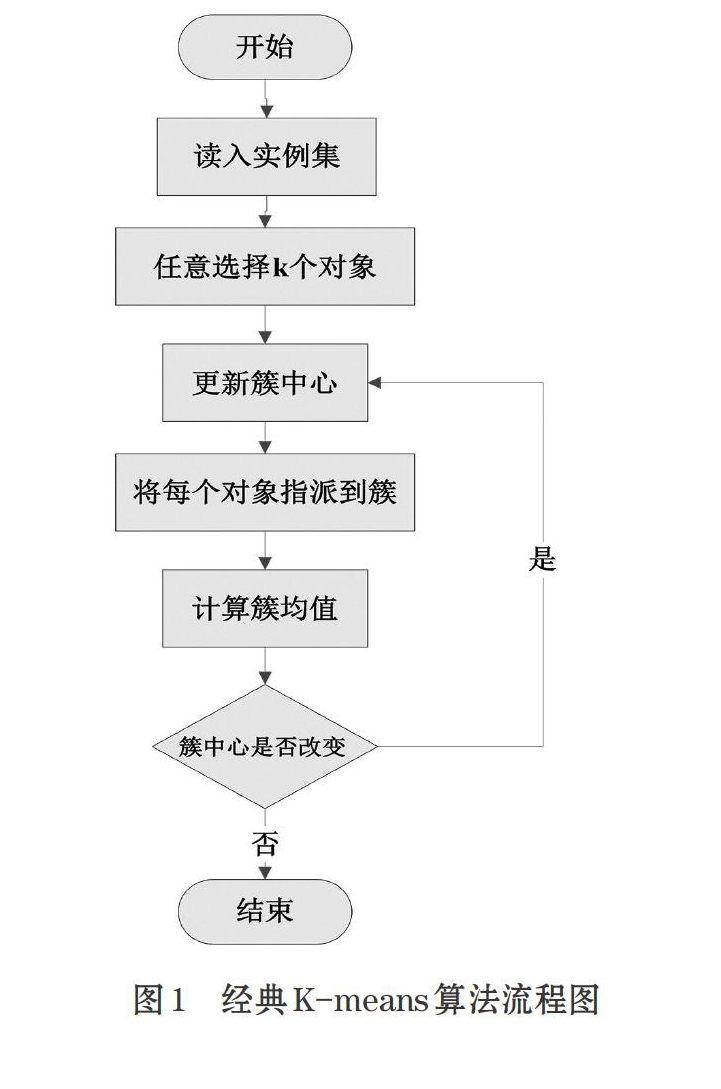
1.2 K-means算法流程描述

经典K-means算法的主要是输入想要划分的数据集C1，C2，C3，C4……Cn，以及需要划分的簇的个数K，经过算法的计算，得到一个将这N个数据划分为M1，M2……Mk的数据簇。目前经典的K-means算法流程图如图1所示。

1.3 K-means算法优缺点分析

K-means算法是采用了迭代式的收缩算法，如果所有数据都不再归到新的簇，则迭代结束。该算法满足了数据挖掘对聚类算法的伸缩性比较好，也即是说方便处理大数据集，对于小的数据集，算法时效性好、对资源的要求也较低，如果类之间的距离差异较大，算法聚类的结果就十分理想。

但是它也有明显的缺点，K-Means算法要求用户提前确定聚类簇的个数K，聚类的效果依赖于用户给定的参数。但是K值在实际运用场景中，由于数据样本的分布不太规则，甚至无法确定数据分布的形态，人们通常无法确定精确的K值。本文针对聚类K-Means算法中K的确定进行改进。

2 改进的K-means算法

2.1 确定最优聚类个数的算法改进思想

经典K-Means算法对于簇的个数K的确定，是用户根据自己的判断来确定的，在实际风电运营管理中，由于测风塔覆冰，传感器异常，由于管理要求弃风等原因均可能形成风电异常数据簇，这样，聚类簇数k的值无法事先精准确定，但可以根据风电运行管理分析，来确定最佳的聚类个数位于某一个范围。改进算法只需要计算类间相似度，选取内间相似度最小的K来作为最优的聚类簇数，从而使K的确定更加准确，获得Kopt。

用Wkm来表示数据簇内所有数据元的相似性，用与Intra（k）来表示数据簇内的所有数据元的相似度，kmax，kmin表示k的最大值、最小值。用Inter（k）来表示两个簇之间的相似度，X代表一个有n个需要聚类的数据集合，Vi代表簇的最开始的聚类中心。因此，根据定义可以得到：

Wkm（k） = Intra（k） +（1- Inter （k） / Inter（kmax））? ⑴

其中：

[Intra（k）=1ki=1kδ（vi）δ（X）]

式⑴中，[δ（X）]表示x中所有数据的相似度，[δ（vi）]表示以vi为中心点的相似度;

[Inter（k）=1ki=1kV（i）]

[V（i）]表示第i个质心与其他簇质心之间的相似度。又据

[d（i，j）≤d（i，h）+d（h，j）]

我们取Wkm（k）达到最小值的K作为最优解 Kopt，且[kmin? kopt ? kmax ]。

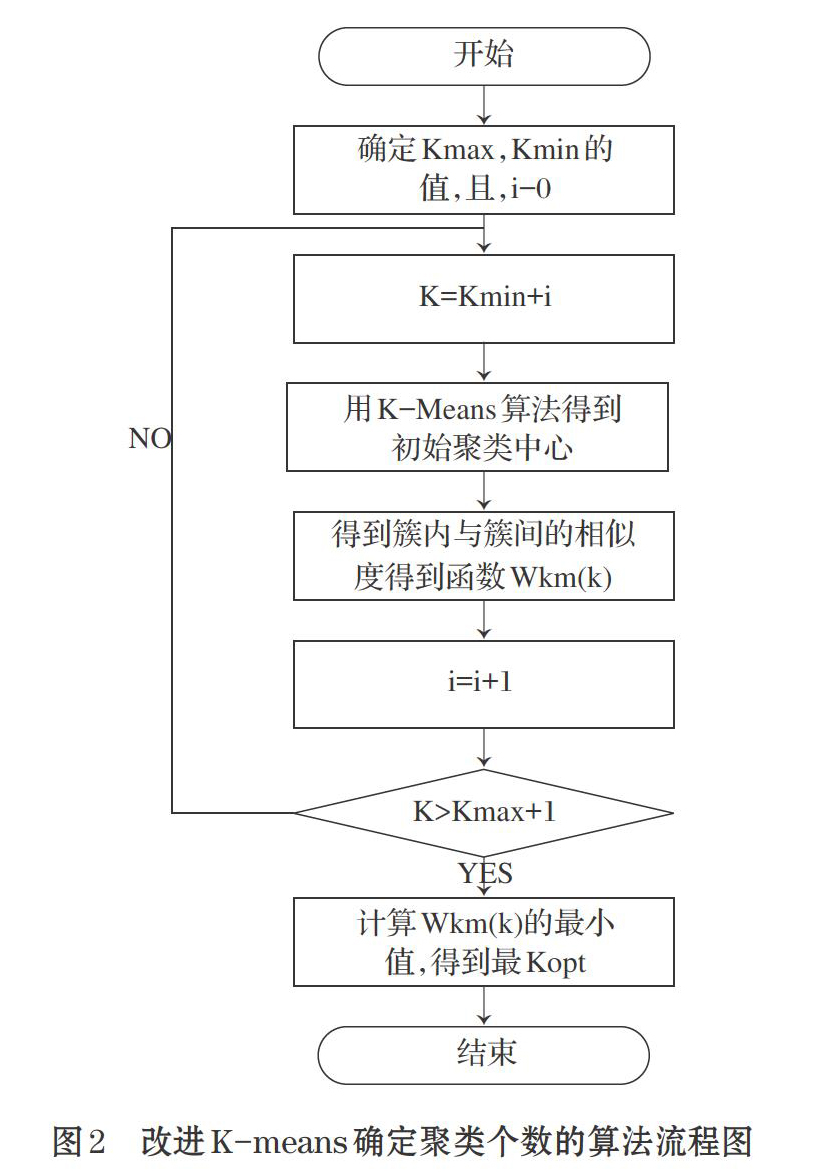
2.2 改进的确定最优聚类个数K的算法流程图

改进的确定最优聚类个数K的算法流程图如图2所示。

[↓][↓][↓][↓][↓][↓][↓][↓] [计算Wkm（k）的最小值，得到最Kopt][YES][NO][开始][确定Kmax，Kmin的值，且，i-0][K=Kmin+i][用K-Means算法得到初始聚类中心][得到簇内与簇间的相似度得到函数Wkm（k）][i=i+1][K[>]Kmax+1][结束]

2.3 改进的确定最优聚类个数算法流程描述

如图2所示，改进的确定最优聚类个数算法流程如下：

⑴ 确定k的最大、最小值Kmax，Kmin;

⑵ 从Kmin为k的初值用K-Means的算法找到初始聚类中心，计算Wkm （k）的值;

⑶ 判断k值得是否大于kmax，如小于Kmin=kmin+1转⑵;

⑷ 取min（Wkm （k））得到Kopt。

3 改进K-means算法在风电异常数据中算法验证

为了验证改进的确定最优聚类个数K的算法的可行性，课题组编制了2.1给出的算法的程序，算法中以2017年10月某电机组以及风电场中测风塔的同步风速和风电功率的历史数据中，选取了通讯故障、人为弃风、风机脱网、正常数据共4组数据来检验。设最小聚类个数为2，最大聚类个数为10，实验结果如表1所示。

从表1数据可以看出，最佳k值为4，与所选取的四种数据相符，结果令人满意。

4 结束语

风电场运营管理需要对测风塔覆冰、信息传输故障、人为弃风等异常数据进行有效识别清洗，以训练风速与功率预报模型。本文对利用K-MEANS算法进行聚类异常数据识别中，无法事先精准确定聚类簇数k值的问题提出改进的三个步骤，首先改进算法要求确定最佳的聚类个数范围，然后对簇进行相似度函数计算，最后取最小的K作为最优的聚类个数，从而缩小了事先确定K的难度。最后选取某风电场的4组数据进行验证，结果达到预期，但相关算法仍需在风电历史实际数据中进一步应用。

参考文献（References）：

[1] 水电水利规划设计院，《中国可再生能源发展报告（2018）》发布[Z].中国水利水电出版社，2019.

[2] 苏杰，李志俊.基于数据挖掘的风电异常数据辨识[J]，黑龙江科技信息，2016.17：144

[3] 杨姝凡，测风塔的测风精度对风电产能的影响研究[D].新疆大学，2017.5

[4] 徐力卫，风电场测风数据分析中有关问题的探讨[J].宁夏电力，2008.6：59-60

[5] Jiawei Han， Micheline Kamber著，范明，孟小峰譯.数据挖掘概念与技术[M].机械工业出版社，2007.

[6] 李东琦.聚类算法的研究[D].成都西南交通大学，2007.5

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。