《聚类算法在出租车合乘方案中的应用》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

聚类算法在出租车合乘方案中的应用

范文

谭艳祥李立军彭家睿徐迅

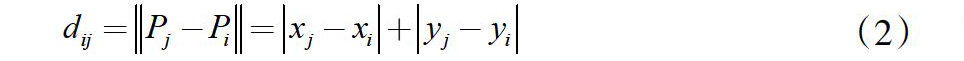
摘? 要：随着乘坐出租车出行的人数不断增加，现阶段的“打车难”却成为人们不得不面对的问题。出租车合乘能有效缓解上下班高峰期打车难的问题，并减少能源浪费和大气污染。文章建立了考虑绕路与三名乘客合乘的静态合乘模型。使用基于势能值和曼哈顿距离的聚类算法对出租车进行聚类，建立了基于非直达系数的合乘费用分摊模型，降低了乘客出行总费用。最后进行仿真实验，对模型的部分细节进行补充说明，实验结果表明合乘使得乘客与司机双方受益。

关键词：出租车合乘;静态;聚类;费用分摊

中图分类号：U491? ? ? ? ?文献标志码：A? ? ? ? ?文章编号：2095-2945（2020）29-0041-04

Abstract： With the increasing number of people traveling by taxi， "difficulty in taking a taxi" at the present has become a problem that people have to face. Taxi pooling can effectively alleviate the problem of taxi hailing during rush hour and reduce energy waste and air pollution. In this paper， a static multiplicative model with detour and three passengers is established. The potential energy value and Manhattan distance clustering algorithm are used to cluster the taxis， and the co-ride cost sharing model based on non-direct coefficient is established to reduce the total passenger travel cost. Finally， a simulation experiment is carried out to explain some details of the model. The experimental results show that co-riding benefits both passengers and drivers.

Keywords： taxi carpool; static; clustering; cost sharing

引言

随着中国经济的发展与城镇化进程的推进，“都市圈”“城市群”正在不断发展。城市的快速扩张，带动了经济的增长，提高了人民的生活质量。但是包括人口膨胀、交通拥堵、环境恶化、资源紧张在内的城市病却制约着城市的发展。目前，如何缓解城市病迫在眉睫，其中上下班高峰时期的交通拥堵问题明显影响了城市生活的体验[1]。作为城市公共交通方式的重要组成部分，城市出租车的重要性逐渐提高。根据国家统计局2018年的数据，中国出租车保有量为1097237辆，其中北京市出租车保有量为70035辆，上海为41881辆。但是出租车的人均占用道路面积却是其它公共交通运输工具的30倍[2]。出租车行业还存在着运营成本偏高、交通拥堵加剧、资源浪费严重、环境污染加剧、合乘收费标准不统一等问题[3]。针对出租车存在的一系列问题，国内外相关人员提出利用拼车或合乘的方式缓解出租车所带来的不利影响。

出租车合乘可以分为静态合乘与动态合乘。覃运梅等人研究了静态组合模式下的出租车合乘问题，在考虑司机和乘客双方利益的基础上建立相应的数学模型，建立乘客合乘查询系统，采用Floyd算法求出最佳行驶路线[4]。程杰等人研究了动态出租车合乘问题，考虑了在乘客组、出租车分类型情况下，引入协调机制，建立了多对多模式的动态出租车合乘模型[5]。丁冉以乘客的出行时间成本和费用成本最小为目标，建立了出租车动态合乘匹配模型，并设计了插入式算法，致力于寻求乘客的出行请求和可乘车辆的最佳匹配[6]。

周和平等人针对多起点到多终点的出租车合乘，构建合乘模型，综合考虑出行者与驾驶员的利益，确定合理的路径选择与费率[7]。刘华杰根据合作博弈相关理论结合出租车合乘的实际情况，引入合作博弈理论以解决出租车合乘费用的分摊问题[8]。考虑行程时间、费用、舒适度对乘客心理决策的影响，通过计算机模拟，分析不同付费比例和交通拥堵率在乘客心理因素影响下对乘客合乘决策的影响[9]。唐方慧该模型以合乘系统中乘客合乘费用最小化，乘客合乘时间最小化以及出租车燃油费用最小化作为目标函数，建立出租车合乘路径选择及费率优化模型，并设计出求解该模型的非支配排序遗传算法[10]。

1 出租车聚类算法

考虑到数据获取的难易程度，本文做出如下假设：假设每一份订單中乘客的人数为一人;假设合乘乘客相互之间没有要求;假设所有乘客起点、终点均在路边，出租车可直接到达;假设乘客不换乘，从起点到终点只坐一辆出租车;假设载客出租车都愿意参与合乘，且初始时刻车内剩余的座位数为三; 假设车辆无故障行驶，忽略乘客上下车的时间，忽略接送乘客以及到达目的地时加减速的影响，不考虑其它影响因素对到达时间的影响。

本文研究的出租车合乘属于静态合乘，建立的是多对多合乘模型。进行合乘匹配时，借鉴了贪心算法的思想，这满足了先下单的乘客先得到服务的要求，避免出现为追求最优解而导致部分乘客长时间等待的结果。

出租车合乘业务需要将路线相近的多名乘客安排在同一组，由一辆出租车按照一定次序接他们上车，并送他们到达相应目的地，匹配模型的第一步是对出租车聚类。本文描述了一种基于势能值和曼哈顿距离的聚类算法，该方法对“空间分布有规律而时间分布无规律”的出租车的聚类效果更好。

1.1 势能值

设数据集为D，其中D={P1，P2，…Pn}，令I={1，2，...，n}，xi表示数据集D中的任意一点，数据点的势能值可定义为：

其中M表示数据对象的质量，||Pj-Pi||表示数据点Pj和Pi之间的距离，dc表示数据点之间的影响程度因子，R表示距离指数，在本文取M=1，R=2，如图1，可以通过改变参数dc来控制数据聚类的范围大小。如图1所示，当dc=1时，与Pi距离不小于3的点给Pi的势能值带来的变化接近于零。当dc=2时，与Pi距离不小于5的数据点对Pi的势能值的影响就非常小了。按照常理，我们一般是对方圆五公里内的出租车聚为一类，因此本文取dc=2。

1.2 数据点之间的曼哈顿距离

定义数据集为D中的数据点Pi（xi，yi）和Pj（xj，yj）之间的曼哈顿距离为dij，其表达式为：

为了得到各个出租车初始位置的势能函数，我们计算所有出租车两两之间的曼哈顿距离。

1.3 聚类中心数量判别值

定义出租车的初始位置为Ti（xi，yi），每辆出租车的势能值为E（Ti），点间距为U（Ti）。设数据集Taxis中各数据点的数据势能为E={E（T1），E（T2），…E（Tn）}，根据数据点势能值的大小进行排序，定义Is={s1，s2，…sn}为数据集Taxis按势能大小非递增排序的下标，则有Es1？叟Es2？叟Esn。定义U（Ti）为不同数据点的之间的“距离”，如式（3）：

3 算例研究

实验数据来自某城市某日某时刻三分钟之内的真实打车需求数据。数据集中有1001名乘客，667辆空载出租车。乘客起点、要求到达的终点以及当前出租车所在位置分布情况如图2所示。

图2中圆圈表示出租车的初始位置，上三角形表示乘客的上车点，下三角形表示乘客的下车点。如图2所示，出租车初始位置，乘客上车点与下车点三者高度重合。放大之后的图3可以看到所有出租车初始位置，乘客上车点，乘客下车点均分布在正方形网格上。从出租车初始位置分布图可以看出，出租车位置总体呈带状、密集分布，放大之后可以看到所有出租车位置均分布在正方形网格上。大部分出租车分布在横坐标从15～30纵坐标从20～35的矩形的由西南至东北的对角线带状区域。

图4中，T479表示编号为479的出租车，P1表示编号为1的乘客。如图4所示三名乘客合乘出租车的合乘路线十分复杂，基于公平性的合乘费用分摊模型中对于三名乘客合乘距离的界定是不够清楚的，合乘距离是指三名乘客同时在车上的移动距离还是指某两名乘客同時在车上的移动距离。基于公平性的合乘费用分摊模型没有给出清晰的定义，因此给分摊费用的计算带来了困难，不方便实际操作。设置该城市常规出租车计费方式：起步里程为2公里，起步价为8元，超出起步里程后的单位里程价格为每公里2.0元。假设出租车的平均速度为每小时30公里。基于非直达系数的合乘费用分摊模型对于乘客一，乘客二所在组每名乘客的费用计算结果如表1所示。

由上述表格可知，司机的收入几乎增加了一倍，三名乘客中有两名乘客的乘车费用降低了。虽然有两名乘客P847的费用不变，但是如果是三名乘客单独合乘的情况，乘客P847需要多等待两分钟，也就是说虽然费用不变，乘客? 仍然从合乘中得到了益处——减少了等待时间。

4 结束语

本文借鉴物理中的场的概念，建立了出租车的势能值，由于聚类中心的势能值大于该类中的其余点的势能值，因此可在散点图中直观地分辨出聚类中心。本文将普通聚类算法中的欧式距离改为曼哈顿距离，使得聚类算法更符合出租车聚类的特点。本文先进行乘客之间的匹配，再进行一组乘客与出租车的匹配。乘客间的匹配允许阀值范围内的绕行，提高了合乘匹配成功率。关于费用分摊问题，本文基于非直达系数建立了一个简单，方便计算的合乘费用分摊模型。文章最后做了仿真实验，对算法进行了实现，结合具体实例说明了合乘匹配，路径规划，费用分摊的结果。

参考文献：

[1]张昂启.城市交通运行效率评价[D].首都经济贸易大学，2014.

[2]杨树森.公交车·出租车[J].北京成人教育，1996（5）：48-50.

[3]肖强.城市出租车合乘匹配理论模型与关键技术研究[D].兰州交通大学，2017.

[4]覃运梅，石琴.出租车合乘模式的探讨[J].合肥工业大学学报（自然科学版），2006（01）：77-79+101.

[5]程杰，唐智慧，刘杰，等.基于遗传算法的动态出租车合乘模型研究[J].武汉理工大学学报（交通科学与工程版），2013，37（01）：187-191.

[6]丁冉.出租车动态合乘匹配问题研究[D].东南大学，2015.

[7]周和平，钟璧樯，彭霞花，等.出租车合乘路径选择与费率优化模型[J].长沙理工大学学报（自然科学版），2011，8（01）：20-24.

[8]刘华杰.出租车合乘费率优化问题研究[D].兰州交通大学，2015.

[9]张薇，何瑞春，肖强，等.合乘模式下司机收入公平模型及仿真[J].交通运输系统工程与信息，2015，15（04）：92-98.

[10]唐方慧.出租车合乘路径选择及费率优化问题研究[D].兰州交通大学，2016.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。