《例说异面直线所成角求法的优化》-理学论文，数学论文-论文范文参考-科学狗论文网

标题

例说异面直线所成角求法的优化

范文

王统文

空间中的角的求法不外乎有两类：一类是将空间角作出后通过解三角形完成，也就是定义法；一类是利用空间向量方法完成求解，也就是向量法.两类解法都有自己的优点与不足，前者优点在于运算略显简捷但作角不易，有时即便将空间角作出也不能求得；后者的优点在于思路比较简单，但运算较为复杂，需要建坐标系时建系难度较大.现举一例，说说两类解法的应用.

例三棱锥P-ABC中，△PAB是正三角形，PA⊥PC，PA=4，PC=BC=42，E，F分别是PA，BC的中点，求异面直线BE与PF所成角的余弦.

初步尝试如图1，BE所在的平面PAB与PF所在的平面PBC的交线为PB，取PB的中点H，过H作HM∥BE，HN∥PF，HM与PA交于M，HN与BC交于N，则直线HM与HN相交所成的锐角就是BE与PF所成的角.按照这种方法得到的角，求其余弦时要先求出MN，这样做较难.

优化方案如图2，连接AF，BE所在的平面PAB与PF所在的平面PAF的交线为PA，由于E在交线PA上，过E作EG∥PF，EG与AF交于点G（易知G是AF的中点），则BE与EG所成的锐角就是BE与PF所成的角.连接BG，在△BEG中求出∠BEG即为所求，这只需要求出△BEG的三条边BE，EG及BG即可.

解法1（平移法）取AF的中点G，连接EG，BG.因为E是AP的中点，所以EG∥PF，所以∠BEG为异面直线BE与PF所成的角.

利用空间向量，也可以求出空间角.用向量法求空间角时，一般先找到三条两两垂直且交于一点的直线，分别以这三条直线作x，y，z轴建立空间直角坐标系后用向量的坐标形式求解；或者选择空间三个不共面的一组向量作为基底向量，用基底向量表示两异面直线的方向向量，于是就可以用空间向量方法完成解答.依据上述基本方法，可探求本题的向量解法.

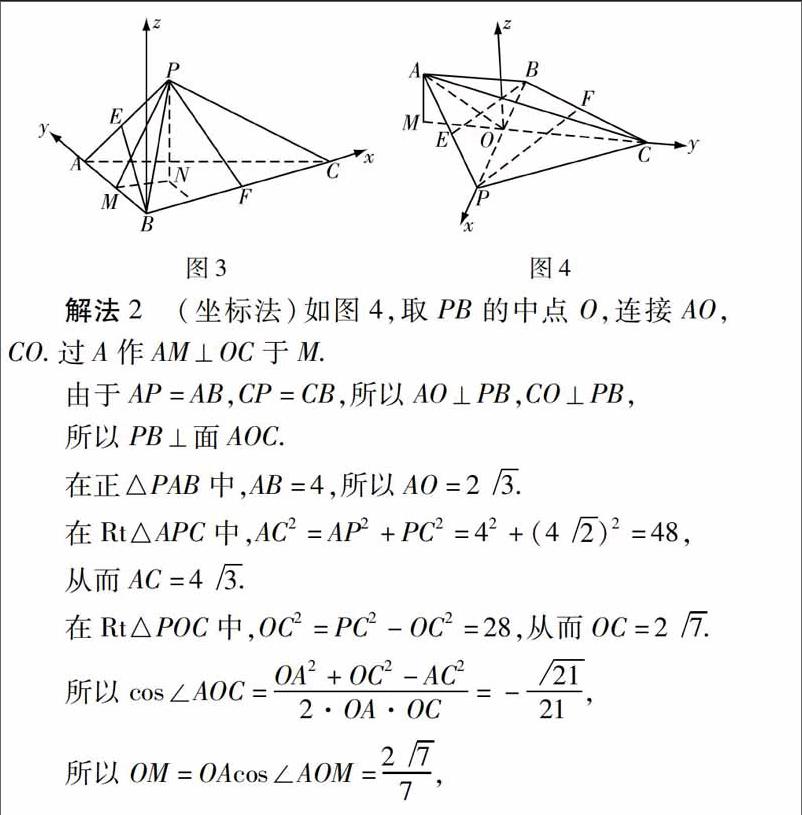
探索1由于AB⊥BC，可考虑以B为坐标原点，BC，BA为x轴、y轴建立空间直角坐标系（如图3）.则A，B，C的坐标就分别为A（0，6，0），B（0，0，0），C（8，0，0）.此时只要能确定点P的坐标，问题就能解决，為此，可过P作PM⊥平面ABC，垂足为N，再过N作NM⊥AB于M，在Rt△PNM中求出PN，MN，但这不容易.考虑到AB=AP，BC=PC，取PB的中点O可以得到AO⊥PB，CO⊥PB等垂直关系.若将三棱锥旋转，以△PBC为底面，则可以点O为原点，PB与OC分别为x，y轴建立空间直角坐标系（如图4），就可以完成解答.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。