《利用pdepe函数和pdetool工具箱求解热传导问题》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

利用pdepe函数和pdetool工具箱求解热传导问题

范文

楚智媛

摘? 要：热传导问题是数学物理方向非常常见的问题。实际生活中的热传导问题通过数学建模都可以转化为偏微分方程（组）问题。由于偏微分方程中含有多元函数的偏导数以及复杂的边界条件，所以求解起来非常困难。该文将详细介绍MATLAB中pdepe函数的用法以及pdetool工具箱的GUI操作界面的使用，并用其求解一维和二维热传导问题。

关键词：热传导;MATLAB;pdepe函数;pdetool工具箱

中图分类号：TK124? ? ? ? ? ? 文献标志码：A

1 热传导问题

热传导问题简单来说就是物体之间或者是系统内存在着温度差，这其中存在着热量的传递。我们在建立热传导方程时，一般使用傅里叶定律和能量守恒定律这2个定律。通过这2个定律我们可以推导出热传导方程（Heat Equation）。我们可以推导出3种维数中的热传导方程（u表示所求函数，t表示时间）。

一维热传导模型公式为：

二维热传导模型公式为：

三维热传导模型公式为：

式中：x，y，z 表示空间直角坐标系下3个方向上的坐标。

偏微分方程学科和广义函数论发展至今，仍有很多偏微分方程（组）无法求解，虽然有些偏微分方程求解起来比较困难，但是该文提到的热传导问题，我们可以使用MATLAB中的内部函数和现成的工具箱来求解。

2 MATLAB中的pdepe函数

MATLAB是由美国MathWorks提出的一种高性能的数学软件，MATLAB中有很多内部函数，都是已经编辑好的程序，我们可以直接拿来使用，而且我们还可以根据自己的需要编写一些我们自己的函数，以便化简编程。pdepe函数就是其中一个非常好用的内部函数，使用它我们可以求解一维偏微分方程（组）问题[1]。

MATLAB中的pdepe函数很好理解，使用起来也很方便，但是在使用它的时候要注意要把微分方程（组）、初始条件、边界条件转化为pdepe函数所规定的一般格式。它的一般格式如公式（1）所示。

式中：m代表参数，这个参数的取值只能是0，1，2。pdex表示问题描述函数即偏微分方程，只是这个函数要写成MATLAB中规定的格式。我们通过改写偏微分方程，将其改为公式（2）的形式。

式中：u表示所求函数，x表示自变量，t表示时间，我们需要求出4个待定系数m，c，f，s。

pdeic表示偏微分方程的初始条件，pdebc表示偏微分方程的边界条件，但是在MATLAB中我们也要按照要求，把边界函数写成pdepe函数要求的形式，如公式（3）所示。

式中：和表示pdepe函数边界条件规定形式下的待定系数函数。在边界条件中我们需要找到pl，pr，ql，qr这4个函数，其中pl和ql为pdepe函数中要求形式下的左边界的函数，pr和qr为pdepe函数中要求形式下的右边界的函数，这里面4个函数的确定是比较难理解的，我们需要弄清这些函数都与那些变量有关系，然后根据题目中给定的边界条件套入公式，从而确定pl，pr，ql，qr。公式（3）中x和t代表函数变量。

我们在利用pdepe函数求解时要注意，pdex，pdeic，pdebc要分别写在3个函数式文件当中，在分别构建好这3个函数式文件之后，我们在回到M文件窗口编写主程序，在主程序中我们可以调用我们之前写好的这3个pdex，pdeic，pdebc函数[2]。

3 利用pdepe函数求解一维热传导问题

要想让热传导方程存在一个确定的解，我们就要给这个方程配上相应的初值条件和边界条件。该文以一维非齐次线性边界条件的热传导方程为例，给出如下问题：有一根细杆，在这个杆上存在着热传导问题，杆的长度为1 m，导热系数为k=0.85 W/（m·k），它的初始分布为u（x，0）=sin（πx），细杆的两端是绝热的，于是它的边界条件为Neumann边界条件，综上所述，该热传导问题可以通过公式（4）求解。

式中：为未知函数关于x方向上的偏导数。

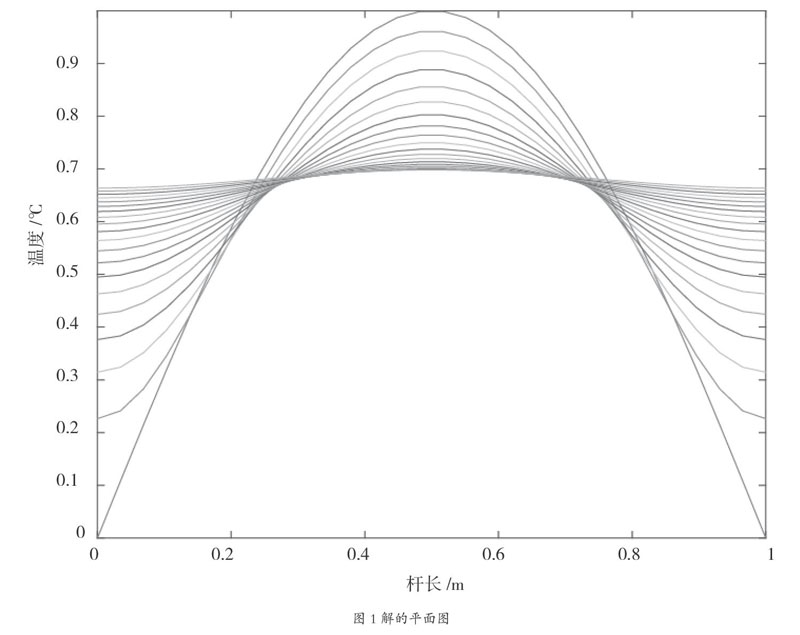
根据列出的方程，我们在MATLAB中要先建立3个函数式文件，分别把方程、初始条件、边界条件按照pdepe函数所规定的样子进行改写，然后写出pdex，pdeic，pdebc函数，然后我们再建立一个命令式文件进行总体编程，然后画出两幅图像。根据MATLAB程序，我们可以得到解的平面图，如图1所示。

由图1我们可以看出，在这根细杆的两端没有热交换，它是绝热的，这个解最后慢慢趋于稳定，最后杆的温度在0.65 ℃左右。

4 MATLAB中pdetool工具箱的使用方法及局限性

MATLAB中的pdetool工具箱能够为偏微分的求解提供很多方便，它通过GUI界面直接选择偏微分方程的條件，然后直接可作出相应解的图像，下面我们详细介绍一下pdetool工具箱的使用方法[3]，其总共分为6步。1）在命令窗口中输入pdetool，进入到GUI界面。2）在pdetool工具箱的工具栏中，有椭圆、矩形等一些图形，可以点击图形进行区域的绘制。所画的区域还可以选择加密，使最后得到的结果更细化一些。3）在菜单栏中有boundary菜单，选择specify boundary conditions，就会出现一个设置边界条件的对话框，这个里面有2种条件，一个是狄利克雷条件，一个是Neumann条件，选择相应的条件，将已知的边界条件代入方程，求出h和r（其中h和r 表示边界条件上的参数）。4）接着点击PDE菜单，选择PDE Specification，就会出现一个设置偏微分方程类型的对话框，里面可供选择的类型有4种，分别是抛物型、椭圆型、双曲型和本征型，根据已知问题的类型，按照给出的规定的方程格式计算出参数c，a，f，d。5）选择Solve菜单，然后选择Solve PDE，我们就可以在GUI界面上看到该偏微分方程的解的图形。6）选择plot菜单，选择parameters，然后会弹出来一个对话框，然后选择我们想要的图形，然后按plot就完成了全部的操作过程。

pdetool虽然可以帮我们求解偏微分方程，但是它也有一定的局限性，比如：它只能求解二维的热传导问题，如果我们想求一维的热传导问题，有限差分法和pdepe函数可能会是首选，如果是三维的，有限差分法可能更好理解一些。所以pdetool工具箱虽然操作简单、好上手，但是还是存在很明显的局限性。

5 结语

热传导问题分为一维、二维和三维。一维的热传导问题我们可以使用的方法比较多，其中pdepe函数是计算比较快而且程序相对比较容易上手的一种方法，针对pdepe函数我们需要做的就是根据要求写出方程、初始条件和边界条件的格式。针对二维的热传导问题，我们也可以使用有线差分法来求解，但是要复杂的多，使用pdetool工具箱，一方面是比较简单、好操作，另一方面也可以直接进行解的可视化。

参考文献

[1]王志强，朱家明.基于Pdepe算法的高温作业防护服装厚度设计[J].淮阴师范学院学报（自然科学版），2019，18（3）：200-205.

[2]贾海峰，刘蕤.线性边界条件热传导方程求解[J].科教文汇（下旬刊），2014（3）：47-50.

[3]李萍，张磊，王垚廷.基于Matlab的偏微分方程数值计算[J].齐鲁工业大学学报（自然科学版），2017，31（4）：39-43.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。