《二氧化硫浓度与颜色读数的多元线性回归模型》-哲学论文-论文范文参考-科学狗论文网

标题

二氧化硫浓度与颜色读数的多元线性回归模型

范文

殷冬琴

摘要：本论述根据实验提供的25组有关二氧化硫浓度与颜色读数的数据，利用EXCEL数据分析工具，建立了二氧化硫浓度与颜色读数GBRSH之间的五元线性回归模型，结果显示该模型拟合程度较好，但是t统计值和P值显示颜色分量RSB对二氧化硫浓度的影响不显著。随后计算颜色分量之间的相关系数，结果显示颜色分量之间存在多重共线性。为此，对建立的五元线性回归模型采用逐步回归法进行优化，统计结果显示出在给定的5个颜色分量GBRSH中，对二氧化硫浓度的影响由主到次的顺序依次为：G>H>B>S>R，可见影响二氧化硫浓度的主要颜色分量为G和H。

关键词：颜色读数;二氧化硫;线性回归;逐步回归

中图分类号：G642.0 文献标志码：A

1概述

随着照相技术和颜色分辨率的提高，人们希望建立物质浓度和颜色读数之间的数量关系。《物质浓度与颜色读数的回归分析》一文根据实验数据，利用向后变量易0除法，建立了组胺、溴酸钾、奶中尿素三种物质的浓度与颜色读数之间的多元线性回归模型。但根据实验数据，用类似的方法讨论二氧化硫浓度与颜色读数之间的多元回归模型时，效果不理想。本论述利用逐步回归法，建立了二氧化硫浓度与颜色读数之间的多元线性回归模型，并且在显著性水平a=0.05下，通过相关系数R2、F检验、t检验对该模型进行了评估，得出在颜色分量RGBsH读数中对二氧化硫浓度影响由主到次的顺序为：G>H>B>s>R，其中红（R）、绿（G）、蓝（B）是颜色的三基色，亮度（B）、饱和度（S）、色调（H）是颜色的三要素，文中实验数据B是指三基色中的蓝色。

2多元线性回归分析

2.1模型建立

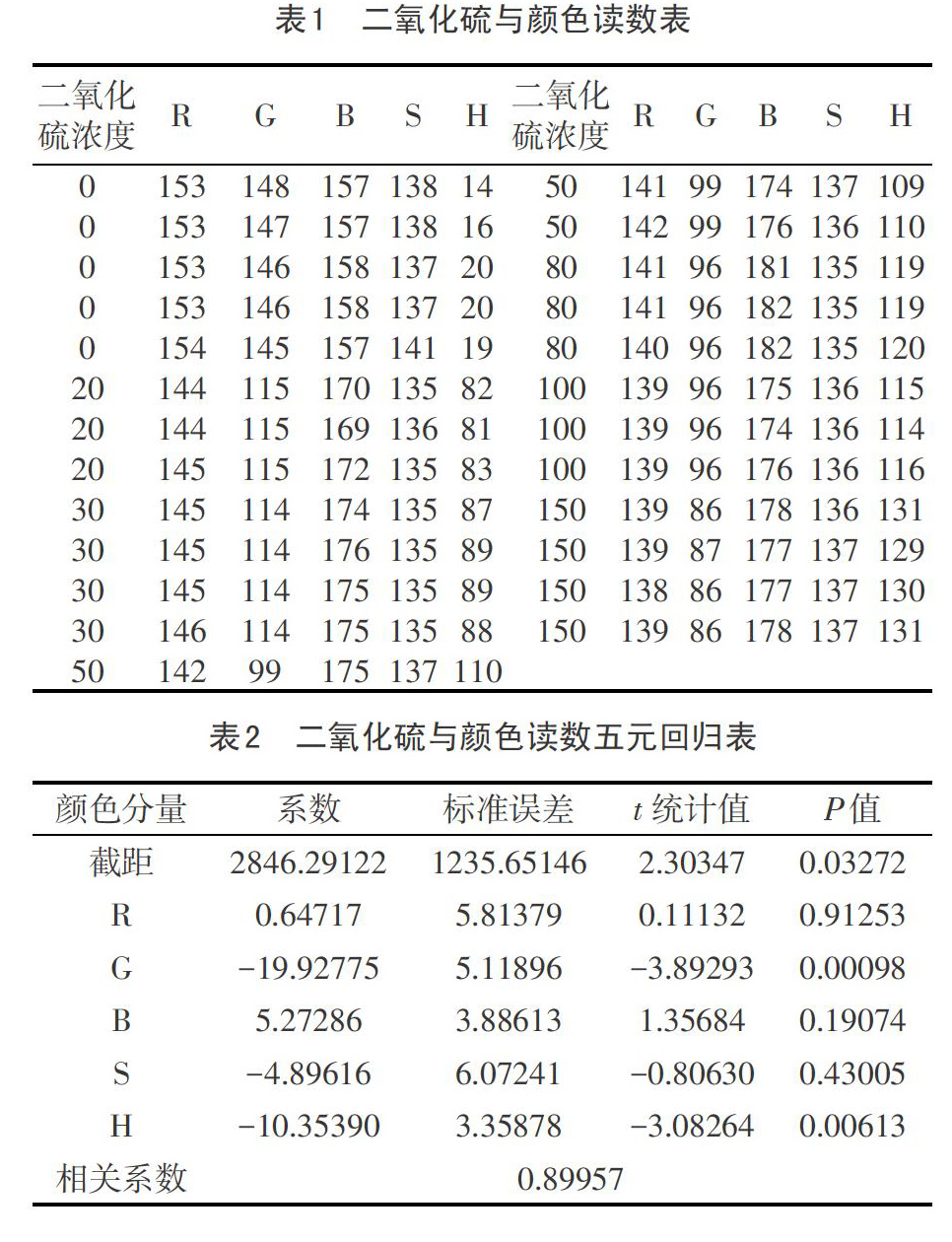
首先整理实验数据，见表1所列。利用ExCEL数据分析工具对表1数据进行回归分析，得到二氧化硫浓度与各颜色分量的五元线性回归结果见表2所列。

从而五元回归方程为：

y=2846.29122+0.64717R-19.92775G+5.27286B-4.89616S-10.35390H （1）

由表2看出，相关系数0.89957，说明方程（1）拟合程度较好，但是t统计值和P值显示颜色分量R、s、B对二氧化硫浓度的影响不显著，造成这一现象的原因可能是数据量或错误，也可能是各颜色分量之间存在多重共线性。下面计算各颜色分量之间的相关系数，结果见表3所列。

表3显示颜色分量R、G之间，R、B之间，R、H之间，G、B之间，G、H之间，B、H之间相关程度都很高，表明确实各颜色分量存在多重共线性。

2.2模型优化

针对上述模型中的多重共线性问题，运用逐步回归的方法对模型进行优化。逐步回归的基本思想是将变量逐个引入模型，每引入一个解释变量后都要进行F检验，并对已经选人的解释变量逐个进行t检验，当原来引入的解释变量由于后面解释变量的引入变得不再显著时，则将其删除。先利用EXCEL数据分析工具，建立二氧化硫浓度分别与各颜色分量RGBSH的一元回归模型，见表4一表8所列。

对于一元线性回归，t值、P值与相关系数检验是等价的，故比较表4-表8的相关系数，可知二氧化硫浓度与颜色分量G拟合最佳，说明RGB三基色中G对二氧化硫浓度的反应最显著，其回归方程为：

y=295.6374-2.15228G （2）

下面以二氧化硫浓度y与颜色分量G的一元回归为基础，依次加入其他颜色分量，进行二元回归分析，具体结果见表9-表12所列。

比较表9一表12的相关系数，F值和t值可知二氧化硫浓度与颜色分量GH的二元回归效果最佳，说明颜色要素SH中的H对二氧化硫浓度的反应最显著。其二元回归方程为：

y=1802.638-11.735G-5.04823H（3）

表12显示相关系数为0.88285，说明模型拟合度较好，但是多元回归还要通过F检验和t检验。F检验：在给定显著性水平a=0.05下，查表可得自由度为k-l=2和n-k=22的临界值F0.05（2，22）=3.443，模型求得F=82.90042>F0.05（2，22），说明方程整体显著，通过F检验;t检验：在给定显著性水平首先a=0.05下，查表可得自由度为n-k=22的临界值为t0.05（22）=1.7171，型求得各颜色分量G、H对应的t统计值分别为：6.03992、-4.95371，绝对值均大于t0.05（22）=1.7171，通过t检验。

以二氧化硫浓度y与颜色分量GH的二元回归为基础，依次加入其他颜色分量，进行三元回归分析，具体结果见表13-表15所列。

比较表13-表15的相关系数，F值和t值可知二氧化硫浓度与颜色分量GHB的三元回归效果最佳，其三元回归方程为：

y=1867.406-17.2342G+5.155534B-8.91935H（4）

表14显示相关系数为0.89576，说明模型拟合度较好，下面进行F检验和t检验。F检验：在给定显著性水平a=0.05下，查表可得自由度为k-1=3和n-k=21的临界值F0.05（3，21）=3.072，模型求得F=60.15237>F0.05（3，21），说明方程整体显著，通过F检验;t检验：在给定显著性水平首先a=0.05下，查表可得自由度为n-k=21的临界值为t0.05（21）=1.7207，模型求得各颜色分量G、B、H对应的t统计值分别为：-4.42757，1.61238，-3.43757，其中G、H的均t计值绝对值均大于to.05（21）=1.7207，通过t检验，但B的t系计值小于t0.05（21）=1.7207说明回归方程（4）中颜色分量B对二氧化硫浓度影响不显著。

以二氧化硫浓度与颜色分量GHB的三元回归为基础，依次加入其他颜色分量，进行四元回归分析，具体结果见表16-表17。

比较表16-表17的相关系数，F值和t值可知二氧化硫浓度与颜色分量GBSH的四元回归效果佳，其四元回归方程为：

y=2864.877-19.8835G+5.496888B-4.60243S-10.4529H（5）

表17显示相关系数为0.8995，说明模型拟合度较好。F检验：在给定显著性水平a=0.05下，查表可得自由度为k-1=4和n-k=20的临界值F0.05（4，20）=2.886，模型求得F=44.7526>F0.05（4，20），说明方程整体显著，通过F检验;t检验：在给定显著性水平首先a=0.05下，查表可得自由度为n-k=20的临界值为t0.05（201=1.7247，模型求得各颜色分量G、B、S、H对应的t统计值分别为：-3.99595，1.695899，-0.86311，-3.31012，其中G、H的t统计值绝对值均大于to.05（20）=1.7247，通过t检验，但B、s的t统计值小于t0.05（20）=1.7247，说明回归方程④中颜色分量B、s对二氧化硫浓度影响不显著。

综上，得到以下结论：

第一，二氧化硫濃度y与颜色分量的最优回归模型是回归方程（3），即

y=1802.638-11.735G-5.04823H

第二，颜色分量RGBSH中对二氧化硫浓度影响由主到次的顺序依次为：G>H>B>S>R。

第三，颜色分量三基色RGB中，绿色GXCZ.氧化硫浓度影响最显著，蓝色B次之，红色R最弱。颜色要素SH中，色调H对二氧化硫浓度影响最显著，饱和度S次之。

3模型不足

本论述中得到的最优线性回归模型显示二氧化硫的浓度仅与两个颜色分量GH的读数关系显著，与其他三个颜色分量RBS关系不显著，造成这一结果的原因可能是提供的实验数据量不足或有错误数据，也可能是实验数据更适合非线性回归的讨论，后续将进一步探讨。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。