《投篮运动的最优方案数学模型》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

投篮运动的最优方案数学模型

范文

摘要：本文首先研究投篮运动的普遍规律，建立数学模型，从而求得投篮的最佳角度，结合matlab软件进行验证，得出最佳入篮角的范围，以及最佳投篮距离和速度。

关键词：投篮速度；投篮角度；投篮命中率；入篮角

Abstract：This paper studies the common law of shooting sports，establish mathematical model，obtained the best shooting Angle，combined with matlab software，the scope of the best Angle of into the basket and best shooting distance and speed.

Key words：Shooting speed；Shooting Angle；shooting average；Come in for the Angle

一、问题分析

通过对篮球运动轨迹及方程的研究，设计投篮的最优方案。需要讨论投篮时球心与篮筐中心距离，球心所处高度以及投球速度之间的变化对球命中率的影响。把其简化成物理学上的斜抛运动，对其水平上用匀速运动讨论运动规律，在垂直方向以初速度为投球时的速度v，加速度为g做匀减速运动，讨论其运动规律。综合求解出其运动轨迹，利用导数意义，求出所需高度，速度等变量的最值，得出最佳投篮点和投篮角度。

二、模型假设

假设空气的阻力、主观因素对运动员投篮影响、篮球出手后球自身的旋转可忽略；假设篮球的运动轨迹和篮筐中心在同一平面内。

三、符号说明

四、模型建立与求解

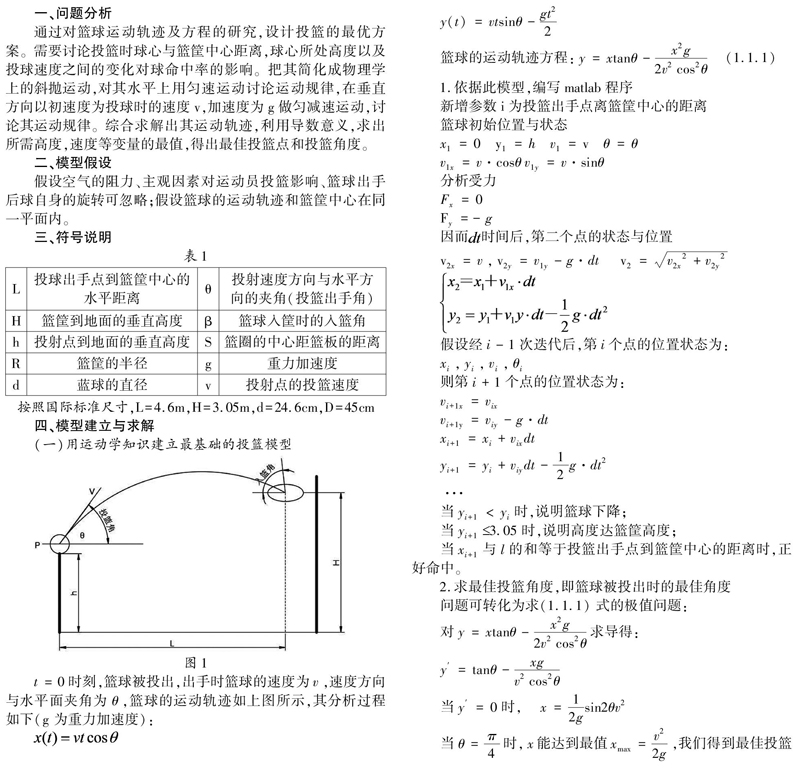
（一）用运动学知识建立最基础的投篮模型

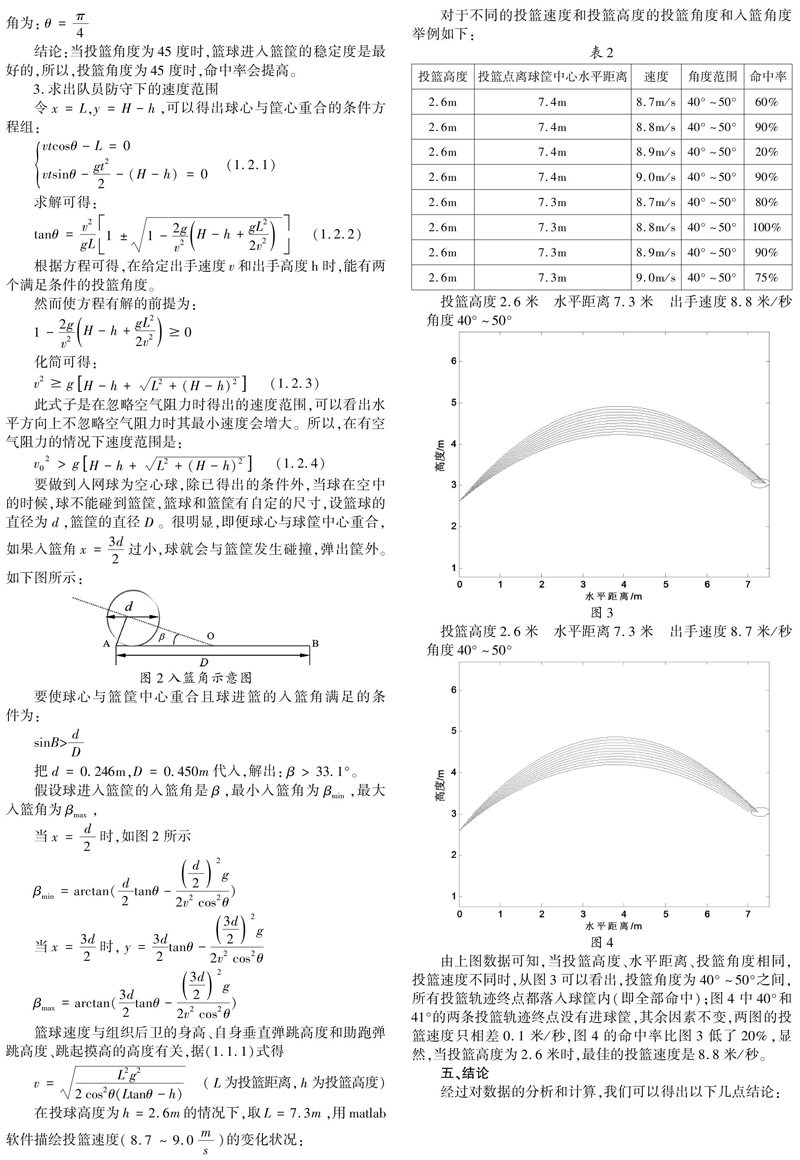
由上图数据可知，当投篮高度、水平距离、投篮角度相同，投篮速度不同时，从图3可以看出，投篮角度为40°～50°之间，所有投篮轨迹终点都落入球筐内（即全部命中）；图4中40°和41°的两条投篮轨迹终点没有进球筐，其余因素不变，两图的投篮速度只相差0.1米/秒，图4的命中率比图3低了20%，显然，当投篮高度为2.6米时，最佳的投篮速度是8.8米/秒。

五、结论

经过对数据的分析和计算，我们可以得出以下几点结论：

（1）分析数据可以得出，当投篮高度、水平距离、投篮角度保持不变，投篮速度不同时，速度越大，投篮命中率越高。

（2）速度一定时，投篮高度越大，投篮角度应越大，但随着速度的增加，高度对角度的影响变小，这种情形在1度左右；投篮高度一定时，速度越大，投篮角度也应越大，速度的影响在 7～9度左右。

（3）投篮角度和投篮速度的允许偏差总的来看，允许偏差都比较小；进一步分析可知，投篮高度一定，速度越大，角度的允许偏差越小，速度的允许偏差越大，且对角度的要求比对速度的要求严格，投篮速度一定，高度越大，虽然也是高度的允许偏差越小，速度的允许偏差越大，但这时角度和速度的要求都相对较低。

（4）出手髙度达到2.6～2.9米时各种距离的出手角度趋向稳定。

六、模型评价与推广

本文通过对影响投篮各个因素进行详细分析，给出了队员不同投篮速度和投篮角度，提高投篮命中率对这两者的要求。运用了数字、表格和文字说明以及MATLAB软件等来说明如何选取投篮最佳出手点及最佳角度这一实际问题，更科学实际地分析了在投球过程中的几个主要条件对命中率的影响。此外，模型所用的公式计算可得出适合投篮的最佳出手角度范围和速度范围，使这三者之间的相互关系有了一定的联系建立的模型能与实际紧密联系，推广性较强。

参考文献：

[1]张宏杰，陈钓.篮球运动[M].北京：北京體育大学出版社，2004，11-15.

[2]川川.投篮问题的数学建模，百度文库，2012.

[3]苏之品.篮球投射的数学模型.

[4]赵凯华.罗蔚茵.力学[M].北京：高等教育出版社，2004：26-27.

[5]沉继红等编著.数学建模.哈尔滨工程大学出版社，1998.

[6]肖宇谷.数学，北京：中国财经经济出版社，2010.

[7]郭鼎文.投篮的技巧[M].北京：北京体育大学出版社，2017.

作者简介：董晓红（1983-），女，汉族，内蒙古包头人，理学硕士，讲师。

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。