《基于Simulink的列车垂向振动仿真分析》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

基于Simulink的列车垂向振动仿真分析

范文

孔程程　张静　黄兵

摘要：为研究轨道车辆在轨面激扰下的运行平稳性，根据车辆运行特性与车辆构造原理，本文建立列车转向架-车体耦合的四自由度垂向振动模型，利用Simulink建立该系统的仿真模型，对车辆以两种速度通过轨道激扰时车体各性能指标的响应进行研究。此外，为抑制轨道车辆车体的弹性振动，在车体底架下安装动力吸振器，建立有动力吸振器的优化振动模型，分析动力吸振器对列车垂向振动性能的影响。通过分析仿真结果可知，优化后的振动模型能够有效减少车辆的垂向振动，进一步提高轨道车辆运行的平稳性。

关键词：垂向振动模型;Simulink仿真;动力吸振器;运行平稳性

中图分类号：U270 文献标识码：A 文章编号：1003-5168（2020）14-0008-03

Simulation Analysis of Train Vertical Vibration Based on Simulink

KONG Chengcheng ZHANG Jing HUANG Bing

（School of Mechatronics and Vehicle Engineering， Chongqing Jiaotong University，Chongqing 400074）

Abstract： In order to study the running stability of rail vehicles under the disturbance of the track surface， according to the vehicle operating characteristics and vehicle construction principles， a four-degree-of-freedom vertical vibration model of train bogie-body coupling was established， Simulink was used to establish the simulation model of the system， and the response of each performance index of the vehicle body when the vehicle passed the track disturbance at two speeds was studied in this paper. In addition， in order to suppress the elastic vibration of the rail car body， a dynamic vibration absorber was installed under the chassis of the car body， an optimized vibration model of the dynamic vibration absorber was established， and the influence of the dynamic vibration absorber on the vertical vibration performance of the train was analyzed. By analyzing the simulation results， it can be seen that the optimized vibration model can effectively reduce the vertical vibration of the vehicle and further improve the stability of the rail vehicle operation.

Keywords： vertical vibration model;Simulink simulation;dynamic vibration absorber;running stability

大多数发生在车辆上的振动是有害的，过于剧烈的振动不仅会影响车辆运行的平稳性，而且会损害人体健康。现代城市轨道车辆都在往高速轻量化、安全舒适等方面发展[1]，提高列车运行平稳性，降低轨道车辆运行过程的振动，改善轨道车辆的动力性能，已成为当今铁道车辆的热点。因此，建立适当的模型来研究车辆运行状况和减小车辆运行过程中的振动是十分必要的。曾京提出在铁道客车系统引用动力吸振器从而降低客车垂向振动的理论研究[2]，陈小花对具有动力吸振系统和半主动控制系统的轨道车辆进行了动力学仿真研究[3]。由于轨道车辆的振动系统十分复杂，本文主要研究能较好反映车辆振动系统特性的车辆垂向简化振动模型。

1 车体-转向架垂向动力学模型的建立

1.1 轨道车辆四自由度垂向振动物理模型

根据轨道车辆的实际组成结构，建立车辆的简化垂向振动模型，如图1所示。车辆垂向振动模型中，转向架通过一系悬挂的弹簧和阻尼与轮对耦合，车体通过二系悬挂的弹簧和阻尼与转向架耦合[4]。

图1中，车辆以速度[v]行驶在轨道上，其中车体质量为[mc]，前后转向架的质量分别为[mb1]和[mb2]，一系悬挂的刚度和阻尼为[k2]和[c2]，二系悬挂的刚度和阻尼為[k1]和[c1]。垂向振动模型包括车体沉浮[zc]、车体点头[θ]、前转向架沉浮[zb1]和后转向架沉浮[zb2]等四个自由度，以[z0]表示轨面的激扰，由于前后轮间存在车辆定距，因此前轮的激励与后轮的激励存在一定的延时，分别用[z1（t）]和[z1（t-τ）]表示。

为了使模型更容易理解，本文对物理模型进行了简化，保留主要因素，忽略次要因素，并做出了以下两点假设：不考虑轮对的刚度和阻尼，将轮对与轨道视为一体，轨道激扰通过轮对直接作用在连接转向架和轮对的一系悬挂弹簧和一系悬挂阻尼上;只考虑列车垂直方向的振动，不考虑横向和其他方向的振动。

初始时刻，车体垂向位移、车体垂向速度、车体俯仰转角、车体俯仰角速度、前后转向架垂向位移和前后转向架垂向速度都为0。

1.2 轨道车辆垂向振动的数学模型

由牛顿第二定律对垂向振动物理模型进行受力分析，可得以下微分方程。车体沉浮运动的微分方程为：

[mczc+2c1zc-c1zb1-c1zb2+2k1zc-k1zb1-k1zb2=0] ? ? ? ? ? ? ? ? ? ? ?（1）

车体点头运动的微分方程为：

[Jcθ+k1（θL/2-zb2）L/2+c1（θL/2-zb2）L/2+k1（θL/2+zb1）L/2+c1（θL/2+zb1）L/2=0] ? ? ? ? ? ? （2）

式中，Jc为车轮绕其旋转轴的转动惯量。

前转向架沉浮运动的微分方程为：

[mb1zb1+k1（zb1-zc）+c1（zb1-zc）+k2zb1-z1（t）+c2zb1-z1（t）+k1θL/2+C1θL/2=0] ? ? ? ? ?（3）

后转向架沉浮运动的微分方程为：

[mb2zb2+k1（zb2-zc）+c1（zb2-zc）+k2zb2-z1（t-τ）+c2zb2-z1（t-τ）-k1θL/2-c1θL/2=0] ? ? ?（4）

數学模型中，[z1（t）]表示路面激励[z0]通过前轮向前转向架的一系悬挂输入激励，[z1（t-τ）]表示路面激励[z0]通过后轮向后转向架的一系悬挂输入激励，[τ]为后位车轮激励对前位车轮激励的时间滞后，其计算公式为：

[τ=Lv] ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （5）

2 Simulink仿真模型的搭建

2.1 路面激励的确定

根据轨道几何不平顺理论，轨道的激励可以用单个简谐波或者多个谐波来近似描述[5]。轨道几何不平顺包括车体不平顺、线路不平顺和波形损耗不平顺[5]，因此，可以用车体不平顺谐波、线路不平顺谐波和波形损耗不平顺谐波的线性组合来表示轨道不平激励，本文采用文献[6]通过数值拟合方法得到的三谐波叠加轨道激励，其组成如下：

[z0=0.003 4-0.003cos18.84t-0.000 3 cos188.4t-0.000 1cos376.8t] ? ? ? ?（6）

由于前后转向架存在车辆定距，当轨道车辆以一定速度运行时，从后轮输入的激励相对于前轮输入的激励存在一个延时时间[τ]，用Simulink中的Transport Delay模块实现激励的时间延迟。

2.2 垂向振动模型仿真

根据垂向动力学模型，分别搭建车体沉浮运动子系统、车体点头运动子系统、前转向架沉浮运动子系统、后转向架沉浮运动子系统和总成子系统，分别将其封装成子模块。根据微分方程将个子模块相互连接起来，输入轨道不平顺激励，得到四自由度车辆垂向振动仿真模型。

2.3 Simulink时域仿真与结果分析

为研究轨道车辆的振动性能，分别对车辆运行速度速为20 m/s时、100 m/s时两种情况进行仿真。根据式（5）可以计算出前后轮激励的滞后时间分别为0.5 s和0.1 s，将Transport Delay模块的延迟时间分别设置为0.5 s和0.1 s。

通过分析两种速度下的仿真结果可知，经过1 s左右的调整后，车体沉浮运动和车体点头运动的时域响应分别进行幅值不同的等幅振动。另外，随着轨道车辆运行速度的增大，车辆垂向位移和垂向加速度的振幅都有一定程度的增加，而车辆俯仰角位移和角加速度振幅的增加并不明显。

3 垂向振动模型的优化

为改善轨道车辆在运行过程中的垂向振动性能，提出在车体下安装动力吸振器，建立基于动力吸振器的五自由度垂向振动优化模型[7-8]。

3.1 物理模型的构建

在四自由度垂向振动模型的基础上，添置一个动力吸振器，即增加了一个自由度。设动力吸振器的刚度质量[mb]为4 000 kg，刚度[k]为[1.93×106N/m]，阻尼系数[c]为[2×105N?s/m]，动力吸振器的垂向位移为[zb]。优化后的物理模型如图2所示。

3.2 基于动力吸振器的垂向振动数学模型

由物理模型可以发现，优化后的模型中动力吸振器与车体的运动产生耦合，因此，只有车体沉浮运动的数学模型改变，车体点头和前后转向架沉浮运动的数学模型均未发生改变。根据牛顿第二定律得到优化设计的垂向振动数学模型，如下所示。

车体沉浮的微分方程为：

[mczc+（2c1+c）zc-c1zb1-c1zb2-czb+（2k1+k）zc-k1zb1-k1zb2-kzb=0] ? ? ? ? ? ? ?（7）

车体点头运动的微分方程为：

[Jcθ+k1（θL/2-zb2）L/2+c1（θL/2-zb2）L/2+k1（θL/2+zb1）L/2+c1（θL/2+zb1）L/2=0] ? ? ? ? ? （8）

前转向架沉浮运动的微分方程为：

[mb1zb1+k1（zb1-zc）+c1（zb1-zc）+k2（zb1-z1（t）+c2zb1-z1（t）+k1θL/2+c1θL/2=0] ? ? ? ? （9）

后转向架沉浮运动的微分方程为：

[mb2zb2+k1（zb2-zc）+c1（zb2-zc）+k2zb2-z1（t-τ）+c2zb2-z1（t-τ）-k1θL/2-c1θL/2=0] ? ? （10）

动力吸振器沉浮运动的微分方程为：

[mbzb+czb-czc+kzb-kzc=0] ? ? ? ? ? ? ? ? ? ? （11）

3.3 有动力吸振器的垂向振动仿真模型

动力吸振器和车体存在耦合关系，车体沉浮运动子系統的仿真模型发生改变，其他三个子系统的仿真模型没有改变。在Simulink模块库中，将各子系统封装成相应的子模块，根据式（7）至式（11），建立带有动力吸振器的垂向振动仿真模型。

3.4 Simulink时域仿真与结果分析

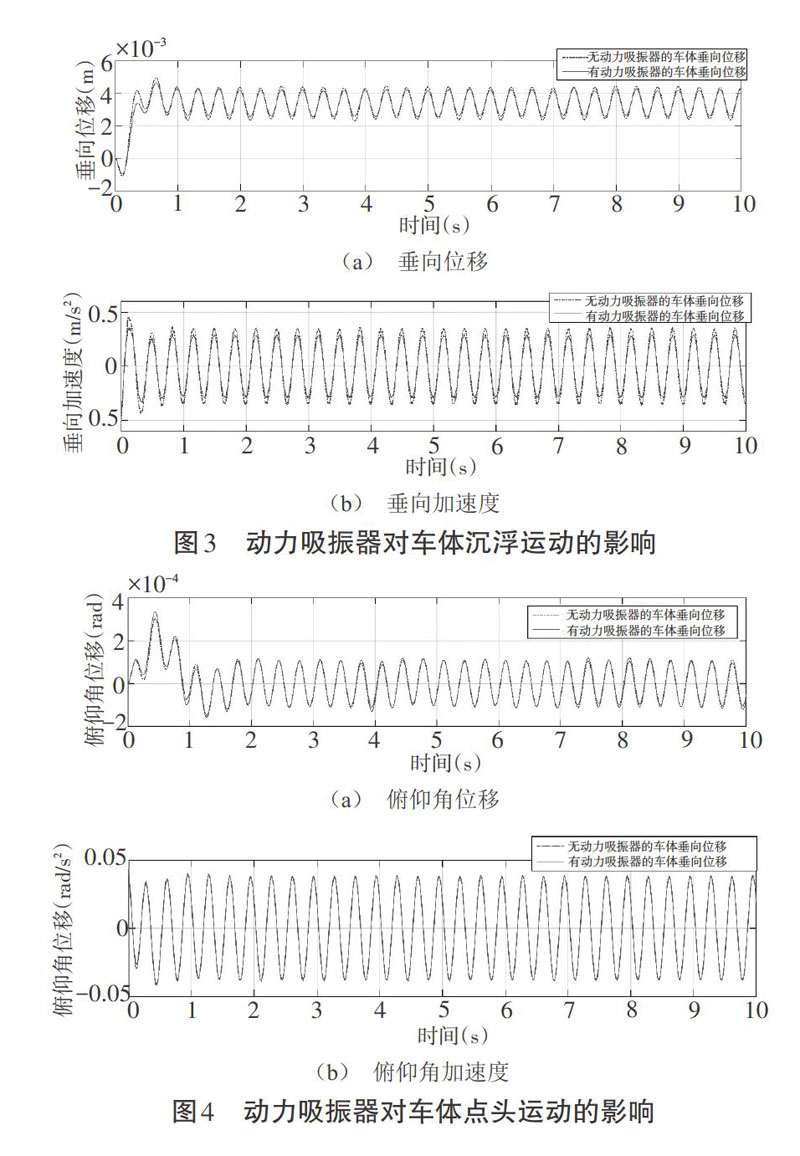
为更直观分析吸振器对振动指标的影响，笔者将初始模型与优化振动模型示波器中仿真图像的数据导入MATLAB工作区，用Subplot和Plot函数画出图3和图4所示的时域响应对比图。

（a）垂向位移

（b）垂向加速度

（a）俯仰角位移

（b）俯仰角加速度

图3是当车速为100 m/s时，在有动力吸振器与没有动力吸振器两种情况下，列车垂向振动位移与加速度的对比图。从图中可以看出，与没有动力吸振器的仿真模型相比，具有动力吸振器的垂向振动仿真模型的振动幅值要相对小一些，减振效果明显。图4是在有、无动力吸振器两种情况下，车体俯仰角位移和俯仰角加速度对比图，由此可以看出，动力吸振器对车俯仰体角位移和角加速度的抑制效果不明显，角位移有细微的抑制作用，但是角加速度几乎保持不变。

通过分析图3和图4可知，列车原有的垂向振动越大，动力吸振器的减振效果就越好。另外，动力吸振器对车体点头运动的抑制效果并不明显，即动力吸振器的减振性能在一定程度上是被限制的。

4 结论

基于原始振动模型与优化振动模型的仿真结果分析，本文得到以下三条结论。轨道车辆以不同的速度行驶在具有谐波输入的轨道上时，较高速度下车体垂向位移和垂向加速度响应幅值较大，车体俯仰角位移和角加速度的响应幅值与低速时相比有微小增加。这说明列车运行速度对车体垂向振动的性能指标有较大的影响。动力吸振器能够在一定程度上减小车体垂向振动位移和加速度的响应幅值，具有较好的减振效果，但对车体点头运动的抑制效果不明显。MATLAB中的Simulink模块功能强大而且操作简单，能够方便、快捷地搭建仿真模型并得到准确的仿真结果。

参考文献：

[1]彭福泰.车辆空气弹簧悬挂系统动力学特性研究[D].兰州：兰州交通大学，2017.

[2]曾京，邬平波，郝建华.铁道客车系统的垂向减振分析[J].中国铁道科学，2006（3）：62-67.

[3]陈小花，张亮，李克峰.基于Simulink仿真模拟车辆垂向振动[J].机械研究与应用，2008（5）：81-82.

[4]翟婉明.车辆-轨道垂向系统的统一模型及其耦合动力学原理[J].铁道学报，1992（3）：10-21.

[5]刘寅华，李芾，黄运华.轨道不平顺数值模拟方法[J].交通运输工程学报，2006（1）：29-33.

[6]包发毅.列车垂向振动数值分析及其电路仿真[D].兰州：兰州交通大学，2017.

[7]牟健.城轨车辆垂向振动鲁棒控制研究[D].兰州：兰州交通大学，2015.

[8]段红杰，宋学谦.列车垂向振动的半主动简谐隔振研究[J].振动与冲击，2007（5）：119-122.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。