《多任务自适应网络的非负参数向量辨识研究》-工学论文，科技论文-论文范文参考-科学狗论文网

标题

多任务自适应网络的非负参数向量辨识研究

范文

王紫璇

摘要：多任务自适应网络是指网络中节点辨识的参数向量不完全相同的自适应网络。在一些物理现象中，网络中的参数向量可能会受到非负性条件约束。然而，现有的多任务扩散式LMS算法只适用于辨识无约束的参数向量。为了解决这一问题，选用每个节点的误差信号的三次方的绝对值作为代价函数，并利用KKT条件和随机梯度下降法，推导出一种多任务非负三次方绝对值算法（MD-NNLMAT）。仿真结果表明，在相同的稳态失调下，该算法比多任务非负最小均方算法（MD-NNLMS）有更快的收敛速度。

关键词：多任务;自适应网络;非负性约束

中图分类号：TN713文献标识码：A文章编号：1003-5168（2020）14-0014-04

Research on Nonnegative Parameter Vector Identification of Multitask Adaptive Network

WANG Zixuan

（Suzhou University，Suzhou Jiangsu 215006）

Abstract： Multitask adaptive network refers to an adaptive network in which the parameter vectors of node identification in the network are not exactly the same. In some physical phenomena， the parameter vectors in the network may be constrained by nonnegative conditions. However， the existing multitask diffusion LMS algorithm is only suitable for identifying unconstrained parameter vectors. In order to solve this problem， the absolute value of the cubic power of the error signal of each node is selected as the cost function， and the multitask diffusion nonnegative least mean absolute third （MD-NNLMAT） algorithm is derived using KKT conditions and stochastic gradient descent method. Simulation results show that under the same steady-state offset， the algorithm has a faster convergence rate than the multitask diffusion nonnegative least mean square （MD-NNLMS） algorithm.

Keywords： multitasking;adaptive network;nonnegative constraints

一直以来，传统的自适应滤波器理论侧重于研究单个节点的辨识问题。近几十年来，在计算机网络、通信网络、机器学习等多个领域，诸多学者致力于研究节点间信息的交互，而不是仅仅依靠节点自身的信息。在分布式自适应网络中，每个节点可以利用相邻节点的交互信息进行独立运算，这样可以提高整个网络辨识的准确性。根据节点的协作方式不同，人们可以将网络分为递增式、扩散式和概率扩散式三种自适应网络类型。基于各种结构和自适应滤波框架，人们提出了一系列分布式网络算法。2013年，Chen等人提出了一系列多任务扩散式算法[1]。2016年，Shi提出了一种扩散式仿射投影（DAPA）算法[2]。这些算法有效地拓展了自适应网络的应用范围，提高了信号处理效果。

在一些物理现象中，如浓度场、人口统计等，多任务自适应网络中的参数向量需要满足非负性约束。在非负性约束条件下，自适应滤波算法本质上是求解条件约束下的最优化问题。2011年，Chen提出了非负最小均方（NNLMS）算法及其衍生出的一系列算法[3]，丰富了自适应滤波器的理论。之后，其他学者又提出了指数非负最小均方（Exponential LMS）算法[4]、非负最小四阶矩（Nonnegative Least Mean Forth，NNLMF）算法[5-6]以及基于零范数的非负最小均方（[l0]-NNLMS）算法[7]。

然而，現有的多任务扩散式LMS算法和多任务扩散式RLS算法只适用于辨识无约束的参数向量。因此，本文首先定义节点误差三次方的绝对值为代价函数，然后利用KKT条件和随机梯度下降法推导出多任务自适应网络的节点迭代算法。仿真结果表明，在高斯噪声和均匀噪声两种噪声环境下，该算法的性能都优于多任务自适应网络的非负最小均方算法。

1 多任务自适应网络模型

图1为多任务自适应网络节点示意图，网络的拓扑结构为扩散式。该网络分为四个簇，每个簇估计的参数向量相同，即[woi=woC1]，[i=1，2，3，4，5，6]，[woj=woC2]，[ j=7，8，9，10，11]，[wok=woC3]，[k=12，13，14，15]，[wol=woC4]，[l=16，17，18，19，20]，网络中不同簇估计的参数向量是不同的，即[woC1≠woC2≠woC3≠woC4]，但它们之间存在某种相似性。

图2为网络节点参数向量自适应辨识框图。其中，未知系统的权向量为[w*=w*1，w*2，...w*MT]，[M]为系统的抽头个数。系统的期望信号满足以下条件：

[dn=xTnw*+zn] ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1）

式中，[xn=xn，xn-1，...，xn-M+1T]为输入向量;[zn]为测量噪声。

自适应系统的误差信号可以表示为：

[en=dn-wTnxn] ? ? ? ? ? ? ? ? ? ? ? ? （2）

自适应滤波算法正是通过最小化均方误差来进行迭代更新，进而得到权值的。

2 算法推导

2.1 多任务自适应网络节点代价函数

在图1所示的多任务自适应网络中，定义节点[k]的邻域（包括[k]）为[Nk]，节点[k]所在的簇为[Ck]，在节点[k]的邻域内但不包含[k]的所有节点记为[N-k]。每个节点满足信号模型[dkn=uTknw*+zkn]。

为了建立节点的代价函数[1]，对于相同簇内的节点，定义联合矩阵[C∈?20×20]，其每一个联合参数[c?k]满足以下条件：

[c?k≥0，k∈N??C?c?k=1， c?k=0 for k?N??C?] ? ? ? ? （3）

对于不同簇内的节点，定义相似性矩阵[ρ∈?20×20]，其每一个相似性参数[ρk?]满足以下条件：

[ρk?≥0，?∈Nk＼Ckρk?=1， ρk?=0 for ??Nk＼Ck] ? ? ? ?（4）

所以，网络中某一节点的局部代价函数为：

[Jlockwk=?∈Nk?Ckc?kJwk+η?∈Nk＼Ckρk?wk-w?2] ?（5）

在文献[1]中，[Jwk=Ed?n-xT?nwk2]。文献[8]指出，在绝大多数信号噪声情况下，选用误差的三次方的绝对值作为代价函数要比均方误差效果好。因此，本文选用[Jwk=Ed?n-xT?nwk3]作为代价函数。节点[k]所在的簇[Ck]在第[k]个节点处的代价函数可写为：

[JCkwk=Jlockwk+?∈Ck＼kwl-wol2Rl] ? ? ? ? ? ? ?（6）

其中，[Rk=?∈Nk?Ckc?kRu，?+η?∈Nk＼Ckρk?IL]。对式（6）进行近似，得到[wk-wo?2Rl≈b?kwk-wo?2]。[b?k]为与第[k]个节点相关的非负性参数。采用文献[1]中的方法进行近似简化，最终可以得到节点[k]所在的簇[Ck]在第[k]个节点处的代价函数，可写为：

[JCkwk=?∈Nk?Ckc?kJwk+η?∈Nk＼Ckρk?wk-w?2+?∈N-k?Ckb?kwk-wo?2] ? （7）

对于上式求梯度，并以瞬时值代替期望值，得到以下公式：

[?wJCkwk=-?∈Nk?C（k）c?ksigneke2kx?n+η?∈Nk＼Ckρk?wk-w?+?∈N-k?Ckb?kwk-wo?] ? ? ? （8）

其中，[ek=d?n-xT?nwk]。

2.2 非负自适应滤波算法

在非负性约束下，一个未知系统的最优估计[wo]满足以下条件：

[wo=argminwJ（w）s.t. wi≥0，i∈1，2，...M] ? ? ? ? ? ? ? ? ? ? （9）

利用KKT条件，文献[3]求解出非负自适应滤波算法迭代公式，即

[wk（n+1）=wk（n）+μDwk（n）[-?wJC（k）（wk（n））]] ? ? ? ? （10）

其中，[Dwk（n）]表示以[wk（n）]的元素为对角元素的对角矩阵。将式（8）带入式（10），可得：

[wkn+1=wkn+μDwkn?∈Nk?Ckc?ksignekek2nx?n ? ? ? ? ? ? ? ? ?-μηDwkn?∈Nk＼Ckρk?wkn-w?n ? ? ? ? ? ? ? ? ?-μDwkn?∈N-k?Ckb?kwkn-wo?] ? ? ? ?（11）

其中，[ek=d?n-xT?nwk]。

在分布式网络中，常采用ATC策略对式（11）进行拆分[9]，可以得到如下迭代方程：

[ψkn+1=wkn+μDwkn?∈Nk?Ckc?ksignekek2nx?n ? ? ? ? ? ? ? ? ?-μηDwkn?∈Nk＼Ckρk?wkn-w?nwkn+1=ψkn+1-μDwkn?∈N-k?Ckb?kwkn-wo?] ? ? ? （12）

由于[wo?]是一个未知量，人们将[ψ?（n+1）]作为其估计值。同时，[ψk（n+1）]相比于[wkn]是节点[k]的权值的更优估计，因此将[wkn]以[ψk（n+1）]代替。随着迭代次数的增加，[ψk（n+1）]与[ψ?（n+1）]差别很小，为了减少计算量，将式（12）中的[Dwk（n）]舍去，可得：

[wkn+1=ψkn+1-μ?∈N-k?Ckb?kψkn+1-ψ?n+1 ? ? ? ? ? ? ? =1-μ?∈N-k?C（k）b?kψkn+1+μ?∈N-k?Ckb?kψ?n+1]（13）

定义

[akk?1-μ?∈N-k?C（k）b?ka?k?μb?k，?∈N-k?C（k）a?k?0，??Nk?C（k）] ? ? ? ? ? ? ? ? （14）

因此，最终的MD-NNLMAT算法为：

[ψkn+1=wkn+μDwkn?∈Nk?Ckc?ksignekek2x?n ? ? ? ? ? ? ? ? ?-μηDwkn?∈Nk＼Ckρk?wkn-w?nwkn+1=?∈Nk?Cka?kψ?n+1] ? ? ? （15）

其中，[ek=d?n-xT?nwk]。为了简化系统联合参数，取[a?k=ck?]。试驗中，联合参数、相似性参数选取均采用平均法则，即[c?k=|N??C?|-1，k∈N??C?]，[ρ?k=|Nk＼Ck|-1，?∈Nk＼Ck]。

3 仿真试验

采用MATLAB对算法进行仿真。选取如图1所示的包含4个任务簇和20个节点的分布式网络拓扑结构。

在仿真中，未知系统的长度选为20，每一个节点都可以利用相邻节点的信息进行运算，因而提升了整个网络的鲁棒性。因为相邻簇之间存在相似性，因此使用线性模型[w*C?=w*+ΔwC?，?∈{1，2，3，4}]获取簇[C?]的权值参数向量[10]。四个簇的权值参数向量取值如图3所示。

从图3可以看出，每一个簇选择的参数向量不完全相同，但又包含相同的原始参数向量[w*]，说明这四个簇既是相似的，但又包含了不同，因此比较合理地反映了多任务自适应网络的参数取值情况。

定义输入信号和系统噪声的方差分别为[σ2x]和[σ2z]，输入信号选取均值为0.5，标准差为0.1的高斯噪声，系统噪声分别选取为均值为0.05，标准差为1e-3的高斯噪声和均匀噪声。

采用归一化均方偏差NMSD对算法的性能进行评估，所有的NMSD曲线为20次独立试验取平均的结果。其表达式为：

[NMSD=1N?=14k∈C?10log10wk-wo+C?wo+C?]（16）

其中，[wo+]为没有负值的最优解。由文献[3]可知，经过迭代，最优解中没有负值元素，即负值变为0。

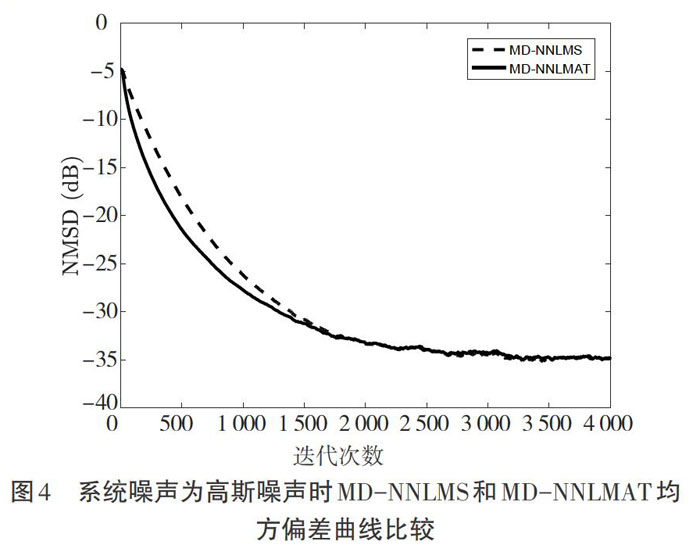
试验一：本试验在高斯噪声环境中，分别使用多任务非负最小均方算法（MD-NNLMS）和多任务非负最小三次方绝对值算法（MD-NNLMAT）进行仿真。为了方便进行对比，尽可能保证算法具有相同的稳态失调，取[μMD-NNLMS=0.015]，[μMD-NNLMAT=0.024]，[η=0.001]。算法收敛性能如图4所示。可以看出，当两种算法的稳态失调相同时，MD-NNLMAT算法比MD-NNLMS算法收敛速度更快。

将收敛后各节点的权值取平均，与原始参数向量[w*]的非负形式进行比较，结果如图5所示。

试验二：本试验在均匀噪声环境中，分别使用多任务非负最小均方算法（MD-NNLMS）和多任务非负最小三次方绝对值算法（MD-NNLMAT）进行仿真。为了方便进行对比，尽可能保证算法具有相同的稳态失调，取[μMD-NNLMS=0.015]，[μMD-NNLMAT=0.024]，[η=0.001]。算法收敛性能如图6所示。可以看出，当两种算法的稳态失调相同时，MD-NNLMAT算法比MD-NNLMS算法收敛速度更快。

将收敛后各节点的权值取平均，与原始参数向量[w*]进行比较，结果如图7所示。可以看出，算法的迭代结果较接近准确结果。

4 结语

本文通过选取了节点新的代价函数，运用梯度下降法和KKT条件，推导出了一种多任务自适应网络的非负最小三次方绝对值（MD-NNLMAT）算法。仿真结果表明，在高斯噪声和均匀噪声情况下，MD-NNLMAT算法的性能都优于MD-NNLMS算法。

参考文献：

[1]Chen J，Richard C，Sayed A H.Multitask Diffusion Adaptation over Networks[J].IEEE Journal of Selected Topics in Signal Processing，2013（99）：1.

[2]Shi J，Ni J，Chen X.Variable step-size diffusion proportionate affine projection algorithm[C]//IEEE International Workshop on Acoustic Signal Enhancement.2016.

[3]Chen J，Richard C，Bermudez J C M，et al.Nonnegative Least-Mean-Square Algorithm[J].Signal Processing，2011（11）：5225-5235.

[4]Chen J，Richard C，Bermudez J C M，et al.Variants of Non-Negative Least-Mean-Square Algorithm and Convergence Analysis[J].IEEE Transactions on Signal Processing，2014（15）：3990-4005.

[5]Ni J，Yang J.Nonnegative least-mean-fourth algorithm[C]//5th IET International Conference on Wireless，Mobile and Multimedia Networks.2013.

[6]Ni J，Yang J，Chen J，et al.Stochastic behavior of the nonnegative least mean fourth algorithm for stationary Gaussian inputs and slow learning[J].Signal Processing，2016（128）：18-27.

[7]Zhao K，Ni J，Chen X.Improved nonnegative adaptive filtering algorithms[C]//IEEE International Workshop on Acoustic Signal Enhancement.2016.

[8]K Xiong，S Wang，B Chen.Robust Normalized Least Mean Absolute Third Algorithms[J].IEEE Access，2019（7）：10318-10330.

[9]Sayed A H.Diffusion Adaptation over Networks[J].Academic Press Library in Signal Processing，2012（5）：323-453.

[10]朱亚楠.鲁棒自适应网络研究[D]苏州：苏州大学，2018.

随便看

科学优质学术资源、百科知识分享平台，免费提供知识科普、生活经验分享、中外学术论文、各类范文、学术文献、教学资料、学术期刊、会议、报纸、杂志、工具书等各类资源检索、在线阅读和软件app下载服务。