“反例法”在中学数学解题中的应用

    张庆大

    

    

    [摘要]在数学解题中应用“反例法”可以有效提高解题效率，拓宽解题思路.教师在课堂教学和问题训练中应让学生充分体会反例，进一步训练学生的辩证思维.

    [关键词]中学数学;反例法;解题

    [中图分类号]

    G633.6

    [文献标识码] A

    [文章编号] 1674-6058（2020）17-0014-02

    在数学教学中，师生往往是指出正确的命题，并专注于获得正确的解决方案，而忽略了如何找出错误.举反例是发现并纠正错误的普遍方式.反例可以丰富和深化学生的抽象理解，特别是对一些数学理论的掌握大有裨益;反例也可以形成清晰认知，特别是对数学性质、概念、定理等的理解.教师列举的反例必须遵循从一般到特殊的原则，并具备形象化、直观性、代表性等诸多特性，使学生容易学习、掌握、理解，学生的感知印象能够在理解反例中得以增加，使学生透彻理解所学的知识.

    一、反例的概念

    在数学中，反例一般指的是对某理论和概念的结论相反的例子，但其条件完全相同.从某种程度上说，所有例子都可以作为反例来使用，因为它总是可以指出一定的命题是错误的.然而，我们所研究的反例，它是一种基于已在数学领域被证明并且具有一定作用的理论和逻辑推理的反面教材.一个反例可以看作是证明的特殊方法.一般来说，反例有许多个，我们列举反例时，只需要选出其中的一个就可以了.数学的反例可以分成下面的几种.

    1.基本形式的反例

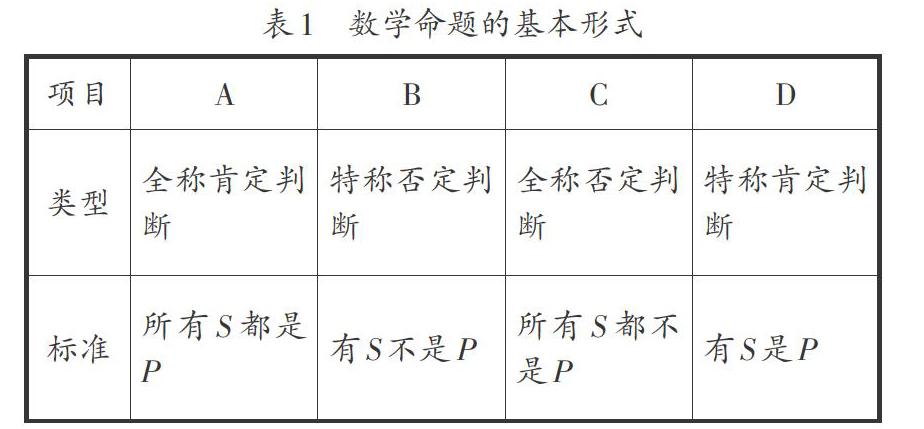
    数学命题可以分成四种基本的形式：全称否定判断，全称肯定判断，特称否定判断，特称肯定判断.（如表1）.

    2.关于必要条件假言判断和充分条件假言判断的反例

    充分条件就是某種事物是另一种事物的充分条件，前者可以推出后者.能够表述为“P→Q”，即“有P必然有Q”.反过来“没有P，不一定说明没有Q”.能够举出反例“没有P，却可以有Q”.这种反例则称为关于充分条件假言判断的反例.

    必要条件就是某一种事物是另一种事物的必要条件，后者能推出前者.能够表述为“P Q”，也就是说“没有P，一定没有Q”，但是“有了P，却不一定有Q”.能够举出反例“有了P，没有Q”.

    3.条件变化型反例

    条件变化型反例是在数学命题中的条件改变后发生的，且结论与原先条件下会有不同，条件的变化可以分为较多的形式.如命题条件的增减以及相应参数的改变.这样的反例形式对于教学和理论的研究有着较大的作用.

    二、反例的作用

    通过举出反例的方法，可以进一步促进新的方法和概念的产生.在数学的历史发展过程中，很多理论的更新以及创造都是由反例得出的.这也让反例在数学领域不断被应用，并起到重要的作用.在数学定理和概念中有许多结构复杂的情况，贯穿其中的结论，有时很难理解.反例可以使概念更加清晰、明确，并能使定理、结论之间的充分性和必要性非常明显.数学中有特别多这样的反例.数学是一门严谨的学科，有很强的学科性，有自己独特的思维特色和独立的逻辑推理体系，不能仅仅凭借着直观和客观去了解和理解它，这样会对其形成模糊的认知.然而数学教学的过程中，让学生了解严谨的逻辑推理和思维特点的同时，还应该掌握各类的反例，这样才能够使学生牢牢巩固数学基础知识和基本技能，提高数学修养与培养科学思维及创新能力.

    三、构造反例的方法

    1.分类法

    分类是数学思维的一种非常重要的方式.通过将一堆事物进行归类，将其中具有一定特征的事物放到一起的方法就叫作分类法.它可以减少寻找反例的范围，避免盲目使用反例进行论证.如何利用分类法列举出反例就成了关键问题.一般地，可以先把题设条件分成甲、乙两大类，命题成立属于甲类，命题不成立属于乙类;然后再在乙类中举出一个相反的例子.

    [例1]命题“平面外的两条平行线在该平面内的射线是平行线”对吗？为什么？

    分析：这个命题在已经给出的条件下看似正确，但是却没有考虑两条平行线是否与平面平行.这样很容易举出反例进行说明.

    如图1所示，当两条平行线a、b都与平面a垂直时，它们在a内的射影为两个不同点A、B，而不是两条相互平行的线.因此该命题是错误的.

    分类法可以有效识别命题中的条件，并且可以避免遗漏相关条件以至于推出的结论出现错误.

    2.特殊化法

    特殊化法就是在命题的条件下，举出一些较为特殊和极端的例子，以证明该命题是否正确.

    分析：把x=-2代入不等式中可知x=-2是它的一个解，所以B、C、D都不对，故选A.

    由本题x=-2就是B、C、D的一个反例.可以看出举反例是解选择题的一种巧妙方法.

    3.穷举法

    [例3]命题“在△ABC中，BC边上的高AD等于BC，H是垂心，M是BC的中点，则MH+DM=1/2Bc”是否正确？为什么？

    分析：这道题的易错点在于，常规的方法只考虑角B和角C小于90°的情况，而忽略了其他的情况.

    当∠C=90°时，如图2所示.

    关于三角形的命题，在解答时不能只考虑一种角度，而是要考虑多种角度在命题条件下是否成立.

    4.推理分析法

    推理反例主要是通过命题给出的条件，根据相关的理论和原理推出相应的结论.

    这些都是常见的解决实际应用题的方法，对学生的思维训练非常好.国外研究者对于反例的作用早有阐释，并且证明其在应用中可以激发学生去探索数学奥秘.因此，在课堂教学和习题训练中让学生充分体会反例，有利于学生有效学习，能进一步训练学生的辩证思维.

    [参考文献]

    [1]黄建桥巧用反例学习数学：论初中数学教学反例的运用[J]教育界：综合教育研究，2018（1）：77-78.

    [2]卢成，俞春三视图表示的几何体不唯一的另一反例[J]中学数学教学，2017（6）：29

    （责任编辑 黄桂坚）