“概念·思想”——搭建数学思维的生长点

    季庆庆

    

    

    [摘要]在数学教学中，我们可以通过概念、思想为学生搭建函数思维生长点

    [关键词]概念;思想;数学思维

    [中图分类号]

    G633.6

    [文献标识码] A

    [文章编号] 1674-6058（2020）17-0002-02

    函数是学生中考必考的知识点之一，但是由于函数的抽象性，加之又是数与形的结合，导致大部分学生在这一阶段呈现厌学的状态.为了营造灵动的课堂氛围，使教材内容得到直观化的展示，让学生在数学学习中感悟数学价值，活化数学思维，教师要优化教学模式，从而实现初中数学函数教学目标.

    一、借助情境，掌握函数概念

    在新课改的落实中，我们不仅要提高学生对数学知识的掌握能力，还要让学生体验到数学的应用价值.借助情境进行初中函数教学，展开数学应用，可使得学生在函数概念的分析中，学好函数、掌握函数、运用函数.

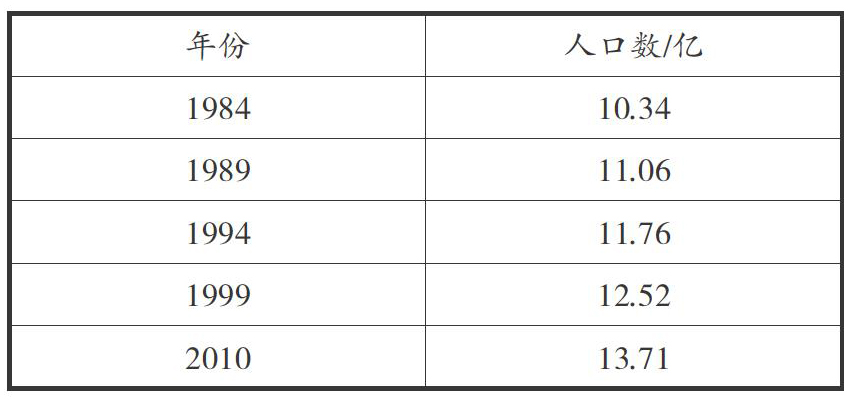
    在教学“函数”概念时，教师可以借助情境，引导学生进行函数概念的探索.如可将我国人口数的统计情况绘制成表格，将年份与人口数分别设为x与y.

    师：人口增长是我们生活中最常见的一个现象，那么在这个图表中，我们把年份设为x，人口数设为y，依据表格你能得出什么结论呢？

    生：每一个年份的变化都有一个对应的人口数的变化.

    师：我们每天都会吃早饭，如果我们喝1碗粥，吃x个包子，每一碗粥1元，每一个包子0.8元，那么我们的早餐费用应该怎么计算呢？其中哪一元素是白变量，哪一元素是因变量呢？

    上述教学中，借助我国人口数量的变化这一直观化情境导入函数，激发学生的探究欲望，以生活化的形式来展开函数概念的教学.在情境探讨中，可以清楚地看到x与y之间的对应变化关系.通过情境，引导学生对白变量、因变量、函数关系式展开分析，既可以帮助学生掌握函数概念，又可以引导学生发现函数变量关系.在变化的过程中催生函数的应用，使得学生在感悟函数概念的同时发展数学思维能力，从而摆正函数学习的态度，提高学习效率.

    二、问题引导，认识函数思想

    教师可以采用问题引导与函数教学相融合的方式开展教学，使得学生领悟到函数思想.

    例如，在教学《一次函数》时，我出示一道函数题：“黄金1号”玉米种子的价格为5元/千克，如果一次性购买2千克以上的種子，超过2千克部分的种子价格打8折.

    （1）填写下面表格.

    （2）写出购买量关于付款金额的函数解析式.

    师：同学们，我们之前学过了函数的概念，在这一问题中是否运用到了函数知识呢？

    生：运用到了.因为在我们购买量变化的同时都有其对应付款金额的变化.

    这一问题不仅是一道函数题，还涉及了学生创造性思维的发展.为此，在解决这一函数问题时，可结合以下活动进行探索.首先，为学生展示玉米种子道具，让学生以小组合作的形式进行分析探索.一个学生称重，一个学生计算.在这一合作活动的体验中，让学生思考付款金额与种子价格的问题.在种子价格不变的情况下进行购买量的探究分析.其次，为学生引入函数知识，就函数y=kx+b、y=kX展开应用.通过0≤x≤2和x>2的分段讨论，得出y=5x，y=4（x-2）+10=4x+2.最后，让学生思考：函数与方程有联系吗？在灵动化问题的融合中实现科学化问题的解决，从而提高学生的问题解决能力.在合作中深化学生的函数思想，在问题解析中让学生对函数的数与形有一个充分的认知.

    三、借助经验，发展学生思维

    为有效发展学生的数学思维，契合生活化数学教学日的，教师可利用生活实例引导学生展开函数问题的分析.在数学函数的分析中，活化学生的思维，为学生数学学习能力的提升奠定良好的基础，从而优化数学三维教学目标.

    例如，小明的妈妈要去超市购物，现在有两个超市实行优惠活动，甲超市购物满50元打9折，乙超市购物满100元打8折，小明的妈妈应该如何购物才会更加优惠？

    这一问题，不仅融合了生活的常识问题，还涉及了方程思想、不等式的思想，它的解决不仅可以提高学生的思维能力，还可以为学生提供多角度分析问题的机会.毕竟一涉及打折的问题，我们就要进行全面的考虑.设购买x元商品，甲超市购物为y1元，乙超市购物为y2元.依据题意可以得出y1=0.9x+5，y2=0.8x+20.方程思想：令y1=y2，解得x=150;不等式思想：令y1>y2，令y1150或x<150，由此可得以下结论：

    （1）当x≤50时，甲、乙者B一样;

    （2）当50

    （3）当lOO

    （4）当x=150时，甲、乙都一样;

    （5）当x>150元时，选择乙.

    师：在解决这一函数问题中运用了哪些知识？在函数、方程、不等式等内容的有机结合中，解题时有哪些需要我们注意的呢？接下来我们一起来总结一下这一数学内容（函数概念一函数思想一函数方程、不等式）

    通过生活案例的分析以及问题悬疑的设置，使学生提高数学思维能力，在思考中激发学生的自主探究欲望，让学生学会运用数学知识解决生活问题，从而实现学生数学知识、数学思维、数学能力协调统一的发展.

    为有效搭建学生的思维路径，使学生在初中函数的学习中认识概念、获得思想、锻炼思维，实现数学学习能力的提升，教师不仅要深入探索数学教材内容，还要充分遵从学生的发展原则，通过对教学过程的优化，使学生在探究分析中达到学以致用的目的，从而实现教学效率的提高.

    [参考文献]

    [1]曹小红.初中数学函数概念起始课的有效教学案例研究[J].数学学习与研究，2018（21）：115-116

    [2]王玉荣.融入生活元素，让初中数学教学焕发生命力[J].新课程（中学），2018（10）：58

    （责任编辑 黄桂坚）