研读图表解决问题
李媛媛


[摘要]结合几道中考数学图表典型例题探讨图表问题的解法,以提高学生把实际问题转化为数学问题的能力,培养学生抽象、概括及分析问题的能力,
[关键词]初中数学,图表,问题
[中图分类号]G633.6[文献标识码]A [文章編号]1674-6058(2020)11-0016-02
在日常生活中,有一类图表信息题,它以其生动的画面,简洁明了的表达,受到师生的欢迎,成为近年中考数学出题的亮点,在解决这一类实际问题时,如能将问题转化为方程,问题解决自然水到渠成,本文采撷几道中考数学题,对其归类例析,以提高学生把实际问题转化为数学问题的能力。
一、器物图示型
器物图示型题目将实物要关注的部分用示意图的形式画出,某些条件就标注在示意图上,学生需要既阅读文字,也观察图形,从而获得对问题的全面了解,画示意图的根本目的在于当用文字不能清楚表达时,借助示意图辅助说明,
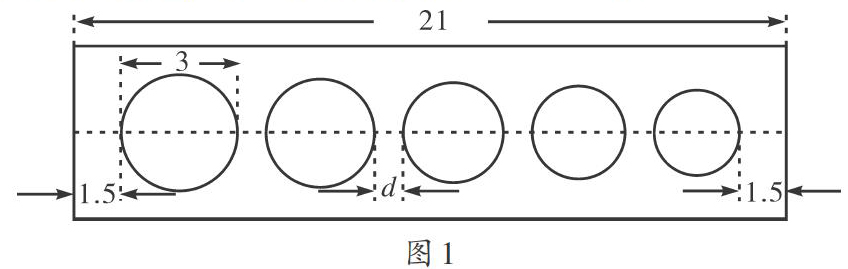
[例1]有一个长方形纸板(如图1),上面有一组大小不等的五个圆孔,它可以用来画圆,其中最左边的圆孔最大,其直径为3cm,右边四个圆的直径都比相邻的左边的圆孔小0.2cm,左、右两边的两个圆与纸板边缘的距离是1.5cm,已知相邻两个圆孔之间的间距相等,那么这个圆的间距是多少呢?
分析:根据右边四个圆的直径都比相邻的左边的圆孔小0.2cm,依次求出其余圆的直径,根据等量关系,5个圆直径长+4个间距+2x1.5=21.列方程求解,
解:其余四个圆的直径依次为:2.8cm,2.6cm,2.4cm,2.2cm。
点评:本题主要考查学生理解题意及识图的能力,5个圆之间有4个间距,间距相等,边距相等,而圆的直径不等,一小段一小段相加等于21.需要注意的是,当问题比较复杂时,学生要善于把问题分类,然后再综合,如本题的21cm可以分为三部分:两个边距、5个直径和4个间距。
二、条件表格型
条件表格型的实际问题是指将问题中的部分条件,以表格的形式给出,学生只有阅读表格才能进一步了解题意,在阅读表格时,先看第一行与第一列的项目(因其表明了表中数据所在行或列的含义);然后依次说出表格中数据的含义;最后将表中的数据进行横向比较与纵向比较,看看有什么结论,
[例2]张小牛同志从大型批发市场买进一些黄瓜与土豆,总质量为40千克,总费用为114元,下面表格列出了黄瓜的批发价与零售价,土豆的批发价与零售价,
(1)张小牛同志买进黄瓜质量是多少?买进土豆质量是多少?
(2)当张小牛同志把这些蔬菜卖完后,减去购买时的费用,他能赚多少钱?
分析:(1)根据“批发土豆的钱数+批发黄瓜的钱数=114元”,列方程求解;(2)根据(1)得出的黄瓜和土豆的质量,再求出每斤黄瓜和土豆赚的钱数,可求出所赚的总钱数,
解:(1)设张小牛同志买进黄瓜质量为x千克,买进土豆质量为(40-x)千克,列方程,得
2.4x+3X(40-x)=114.
解得x=10.
所以张小牛同志买进黄瓜质量是10千克,买进土豆质量是40-10=30(千克),
(2)根据题意得(4-2.4)x10+(5-3)x30=76(元),
所以,黄瓜和土豆全部卖完,他能赚76元,
点评:从表格中,首先要读出黄瓜的批发价和零售价各是多少,土豆的批发价和零售价各是多少;然后根据需要选择数据列方程,在销售问题中,常用到的数量关系有:单价x数量=总价,售价-进价=利润,本题在解答第(1)小题时,实际上有两个数量关系:一是批发土豆的钱数+批发黄瓜的钱数=114元;二是黄瓜的质量+土豆的质量=40千克,需要注意的是,在设未知数时,还要注意方程简洁、易解,
三、设置情境型
设置情境型应用题是指在一定的场景中,通过人物对话、展台等形式,创设一种实际生活的图景,要求学生通过阅读情境,提取有用信息,厘清其中的数量关系,此类型题就像连环画一样,能激起学生学习的兴趣,使数学不再是呆板的数字游戏,而是生动的故事,
[例3]试根据图中信息,解答下列问题,
(2)小明买跳绳的根数比小红少2根,但是小明用的钱却比小红多5元,这是怎么回事?
分析:本题的信息可分为两部分,一是收银台,小明与小红在买跳绳,小明心中有疑问:她付的钱怎么比我还少?二是展台,跳绳每根25元,若超过10根,享受八折优惠,其中展台的信息最关键,(1)根据总价=单价x数量,现价=原价x0.8.列式计算;(2)设小红购买跳绳。根,根据等量关系:小红付款:小明付款-5;列出方程求解,
解:(1)25x6=150(元),
25x12x0.8=300x0.8=240(元),
可见,购买6根跳绳需150元,购买12根跳绳需240元,
(2)设小红买了x根跳绳,则25x0.8x=25(x-2)-5.
解得x=11.
可见,小红购买跳绳11根,
点评:本题所有的条件都在所设的情境中,提取有用信息,找出相等关系是解决问题的关键,根据题中信息可以看出,因为买小于等10根与大于10根的价格不一样,所以买多不一定付的钱多,根据商家的优惠政策,可以组团购买,这样可以节省一些费用,这也是对学生理财观念的培养。
总之,通过对图表型题目的分析,能提高学生把实际问题转化为数学问题的能力,培养学生的抽象、概括、分析及解决问题的能力,当然,学生学会用列方程解应用题的方法后,会自觉摒弃算术法求解,因为用列方程解应用题,容易理解,数量关系明朗,有了方程这个数学模型,就能解决更为复杂的实际问题。

