2016年北京大学博雅计划自主招生数学试题及解答
甘志国
选择题共20小题.在每小题的四个选项中,只有一项符合题目要求,请把正确选项的代号填在表格中,选对得5分,选错扣1分,不选得0分.
1.直线y=-x+2与曲线y=-ex+a相切,则a的值为( )
A.-3B.-2C.-1D.前三个答案都不对
2.已知三角形ABC的三边长分别为a,b,c,则下面四个结论中正确的个数为( )
(1)以a,b,c为边长的三角形一定存在
(2)以a2,b2,c2为边长的三角形一定存在
(3)以a+b2,b+c2,c+a2为边长的三角形一定存在
(4)以a-b+1,b-c+1,c-a+1为边长的三角形一定存在
A.2B.3C.4D.前三个答案都不对
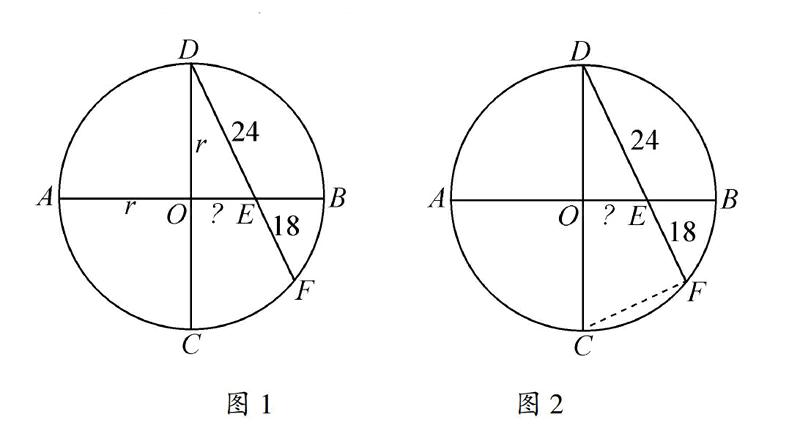
3.设AB,CD是⊙O的两条垂直直径,弦DF交AB于点E,DE=24,EF=18,则OE等于( )
A.46B.53
C.62D.前三个答案都不对
4.函数
f(x)=1p,若x为有理数qp,p与q互素,
0,若x为无理数,
则满足x∈(0,1)且f(x)>17的x的个数为( )
A.12B.13C.14D.前三个答案都不对
5.若方程x2-3x-1=0的根也是方程x4+ax2+bx+c=0的根,则a+b-2c的值为( )
A.-13B.-9C.-5D.前三个答案都不对
6.已知k≠1,则等比数列a+log2k,a+log4k,a+log8k的公比为( )
A.12B.13C.14D.前三个答案都不对
7.cosπ11cos2π11…cos10π11的值为( )
A.-116B.-132
C.-164D.前三个答案都不对
8.设a,b,c为实数,a,c≠0,方程ax2+bx+c=0的两个虚数根为x1,x2满足x21x2为实数,则∑2015k=0x1x2k等于( )
A.1B.0C.3iD.前三个答案都不对
9.将12个不同物体分成3堆,每堆4个,则不同的分法种类为( )
A.34650B.5940
C.495D.前三个答案都不对
10.设A是以BC为直径的圆上的一点,D,E是线段BC上的点,F是CB延长线上的点,已知BF=4,BD=2,BE=5,∠BAD=∠ACD,∠BAF=∠CAE,则BC的长为( )

A.11 B.12 C.13 D.前三个答案都不对
11.两个圆内切于K,大圆的弦AB与小圆切于L,已知AK∶BK=2∶5,AL=10,则BL的长为( )
A.24 B.25 C.26 D.前三个答案都不对
12.f(x)是定义在实数集R上的函数,满足2f(x)+f(x2-1)=1,x∈R,则f(-2)等于( )
A.0 B.12 C.13 D.前三个答案都不对
13.从一个正9边形的9个顶点中选3个使得它们是一个等腰三角形的三个顶点的方法是( )
A.30 B.36 C.42 D.前三个答案都不对
14.已知正整数a,b,c,d满足ab=cd,则a+b+c+d有可能等于( )
A.101B.301C.401D.前三个答案都不对
15.三个不同的实数x,y,z满足x3-3x2=y3-3y2=z3-3z2,则x+y+z等于( )
A.-1B.0C.1D.前三个答案都不对
16.已知a+b+c=1,则4a+1+4b+1+4c+1的最大值与最小值的乘积属于区间( )
A.[10,11)B. [11,12)
C. [12,13)D.前三个答案都不对
17.在圆内接四边形ABCD中,BD=6,∠ABD=∠CBD=30°,则四边形ABCD的面积等于( )
A.83 B.93
C.123D.前三个答案都不对
18.1!+2!+…+2016!除以100所得的余数为( )
A.3B. 13C.27D.前三个答案都不对
19.方程组x+y2=z3,
x2+y3=z4,
x3+y4=z5,的实数解组数为( )
A.5B.6C.7D.前三个答案都不对
20.方程x3+x33+x3+x3=3x的所有实根的平方和等于( )
A.0B.2C.4D.前三个答案都不对
参考答案
1.A.由切点在切线y=-x+2上,可设切点坐标为(x0,2-x0).又切点(x0,2-x0)在曲线y=-ex+a上,可得2-x0=-ex0+a.
再由y=-ex+a,得y′=-ex+a,可得曲线y=-ex+a在切点(x0,2-x0)处切线的斜率为-ex0+a.又切线y=-x+2的斜率为-1,所以-ex0+a=-1.进而可得2-x0=-ex0+a=-1,x0=3,a=-3.
2.B.可不妨设0c.
结论(1)正确:因为可得a+2ab+b>c,(a+b)2>(c)2,a+b>c.
结论(2)错误:2,3,4是一个三角形的三边长,但22,32,42不会是某个三角形的三边长.
结论(3)正确:因为可得a+b2≤c+a2≤b+c2,a+b2+c+a2>b+c2.
结论(4)正确:因为|a-b|+1=b-a+1,
|b-c|+1=c-b+1,|c-a|+1=c-a+1,
所以|a-b|+1≤|c-a|+1,
|b-c|+1≤|c-a|+1,
(|a-b|+1)+(|b-c|+1)≥|(a-b)+(b-c)|+2>|c-a|+1.
3.解法1C.如图1所示,设⊙O的半径为r,由相交弦定理和勾股定理,可得
24·18=AE·EB=(r+OE)(r-OE)=r2-OE2,
242=r2+OE2,
把它们相加后,可求得OE=62.
4.D.由x∈(0,1)知,在f(x)的解析式中可不妨设p,q∈N,p>q,(p,q)=1.
由f(x)>17,可得x=qp,f(x)=1p>17;p=2,3,4,5,6,进而可得
x=12,13,23,14,34,15,25,35,45,16,56
所以满足题设的x的个数为11.
5.A.解法1D.因为x4+ax2+bx+c=(x2-3x-1)(x2+3x+a+10)+(3a+b+33)x+a+c+10,所以由题意,得方程x2-3x-1=0的两个根3+132,3-132均是方程(3a+b+33)x+a+c+10=0的根,所以3a+b+33=a+c+10=0.得a+b-2c=(3a+b+33)-2(a+c+10)-13=-13.
解法2D.由题设,可得(x2-3x-1)(x4+ax2+bx+c).又注意到x4+ax2+bx+c不含x3项,所以x4+ax2+bx+c=(x2-3x-1)(x2+3x-c),x4+ax2+bx+c=x4-(c+10)x2+3(c-1)x+c.
8.B.因为实系数一元二次方程的两个虚数根是一对共轭复数,所以可设x1=r(cosθ+isinθ),x2=r[cos(-θ)+isin(-θ)](r>0).
得x21x2=r(cos3θ+isin3θ),
因为x21x2为实数,所以θ=kπ3(k∈Z),再得
x1x2=cos2kπ3+isin2kπ3≠1
x1x22016=cos2kπ3·2016+isin2kπ3·2016
=cos(2kπ·672)+isin(2kπ·672)=1,
所以∑2015k=0x1x2k=1-x1x220161-x1x2=0.
9.D.这是均匀分组问题,不同的分法种类为
C412C48C443!=5775.
10.A.如图3所示,由∠BAF=∠CAE,∠BAC=90°,得∠EAF=90°.
又因为∠BAD=∠ACD,所以AD⊥BC.得
DE·DF=AD2=BD·DC,
(5-2)(4+2)=2DC,
DC=9,
BC=BD+DC=2+9=11.
图3图411.B.如图4所示,设BK与小圆交于点M,连结ML,设CD为两圆在公共点K处的公切线.
由弦切角定理,得∠BAK=∠DKM=∠KLM.
又因为∠KLA=∠KML,所以∠AKL=∠BKL.
再由三角形角平分线性质,可得ALBL=AKBK,
可求得BL=25.
12.C.在题设所给的等式中分别令x=0,1,-1,
得2f(0)+f(-1)=1,
2f(1)+f(0)=1,
2f(-1)+f(0)=1,
可解得f(0)=f(1)=f(-1)=13.
再在题设所给的等式中令x=-2,得2f(-2)+f(1)=1,所以f(-2)=13.
图513.A.在图5所示的正9边形ABCDEFGHI中,以A为顶角的顶点的等腰三角形有且仅有4个(△ABI,△ACH,△ADG,△AEF),其中有且仅有△ADG是正三角形.
所以所求答案是3·9+93=30.
14.B.考虑a=mn,b=pq,c=mp,d=nq(m,n,p,q∈N*),得a+b+c+d=mn+pq+mp+nq=(m+q)(n+p),所以只要选a+b+c+d是合数即可.
而101,401都是质数,且301=7·43=(1+6)(1+42),
所以取m=1,q=6,n=1,p=42,得a=1,b=252,c=42,d=6,所以本题选B.
15.D.可设x3-3x2=y3-3y2=z3-3z2=m,得x,y,z是关于t的一元三次方程t3-3t2-m=0的三个实数根.
由韦达定理,得x+y+z=3.
16.解法1C.设f(x)=4x+1,得
f′(x)=24x+1,f″(x)=-4(4x+1)-32<0,
选择题共20小题.在每小题的四个选项中,只有一项符合题目要求,请把正确选项的代号填在表格中,选对得5分,选错扣1分,不选得0分.
1.直线y=-x+2与曲线y=-ex+a相切,则a的值为( )
A.-3B.-2C.-1D.前三个答案都不对
2.已知三角形ABC的三边长分别为a,b,c,则下面四个结论中正确的个数为( )
(1)以a,b,c为边长的三角形一定存在
(2)以a2,b2,c2为边长的三角形一定存在
(3)以a+b2,b+c2,c+a2为边长的三角形一定存在
(4)以a-b+1,b-c+1,c-a+1为边长的三角形一定存在

A.2B.3C.4D.前三个答案都不对
3.设AB,CD是⊙O的两条垂直直径,弦DF交AB于点E,DE=24,EF=18,则OE等于( )
A.46B.53
C.62D.前三个答案都不对
4.函数
f(x)=1p,若x为有理数qp,p与q互素,
0,若x为无理数,
则满足x∈(0,1)且f(x)>17的x的个数为( )
A.12B.13C.14D.前三个答案都不对
5.若方程x2-3x-1=0的根也是方程x4+ax2+bx+c=0的根,则a+b-2c的值为( )
A.-13B.-9C.-5D.前三个答案都不对
6.已知k≠1,则等比数列a+log2k,a+log4k,a+log8k的公比为( )
A.12B.13C.14D.前三个答案都不对
7.cosπ11cos2π11…cos10π11的值为( )
A.-116B.-132
C.-164D.前三个答案都不对
8.设a,b,c为实数,a,c≠0,方程ax2+bx+c=0的两个虚数根为x1,x2满足x21x2为实数,则∑2015k=0x1x2k等于( )
A.1B.0C.3iD.前三个答案都不对
9.将12个不同物体分成3堆,每堆4个,则不同的分法种类为( )
A.34650B.5940
C.495D.前三个答案都不对
10.设A是以BC为直径的圆上的一点,D,E是线段BC上的点,F是CB延长线上的点,已知BF=4,BD=2,BE=5,∠BAD=∠ACD,∠BAF=∠CAE,则BC的长为( )

A.11 B.12 C.13 D.前三个答案都不对
11.两个圆内切于K,大圆的弦AB与小圆切于L,已知AK∶BK=2∶5,AL=10,则BL的长为( )
A.24 B.25 C.26 D.前三个答案都不对
12.f(x)是定义在实数集R上的函数,满足2f(x)+f(x2-1)=1,x∈R,则f(-2)等于( )
A.0 B.12 C.13 D.前三个答案都不对
13.从一个正9边形的9个顶点中选3个使得它们是一个等腰三角形的三个顶点的方法是( )
A.30 B.36 C.42 D.前三个答案都不对
14.已知正整数a,b,c,d满足ab=cd,则a+b+c+d有可能等于( )
A.101B.301C.401D.前三个答案都不对
15.三个不同的实数x,y,z满足x3-3x2=y3-3y2=z3-3z2,则x+y+z等于( )
A.-1B.0C.1D.前三个答案都不对
16.已知a+b+c=1,则4a+1+4b+1+4c+1的最大值与最小值的乘积属于区间( )
A.[10,11)B. [11,12)
C. [12,13)D.前三个答案都不对
17.在圆内接四边形ABCD中,BD=6,∠ABD=∠CBD=30°,则四边形ABCD的面积等于( )
A.83 B.93
C.123D.前三个答案都不对
18.1!+2!+…+2016!除以100所得的余数为( )
A.3B. 13C.27D.前三个答案都不对
19.方程组x+y2=z3,
x2+y3=z4,
x3+y4=z5,的实数解组数为( )
A.5B.6C.7D.前三个答案都不对
20.方程x3+x33+x3+x3=3x的所有实根的平方和等于( )
A.0B.2C.4D.前三个答案都不对
参考答案
1.A.由切点在切线y=-x+2上,可设切点坐标为(x0,2-x0).又切点(x0,2-x0)在曲线y=-ex+a上,可得2-x0=-ex0+a.
再由y=-ex+a,得y′=-ex+a,可得曲线y=-ex+a在切点(x0,2-x0)处切线的斜率为-ex0+a.又切线y=-x+2的斜率为-1,所以-ex0+a=-1.进而可得2-x0=-ex0+a=-1,x0=3,a=-3.
2.B.可不妨设0c.
结论(1)正确:因为可得a+2ab+b>c,(a+b)2>(c)2,a+b>c.
结论(2)错误:2,3,4是一个三角形的三边长,但22,32,42不会是某个三角形的三边长.
结论(3)正确:因为可得a+b2≤c+a2≤b+c2,a+b2+c+a2>b+c2.
结论(4)正确:因为|a-b|+1=b-a+1,
|b-c|+1=c-b+1,|c-a|+1=c-a+1,
所以|a-b|+1≤|c-a|+1,
|b-c|+1≤|c-a|+1,
(|a-b|+1)+(|b-c|+1)≥|(a-b)+(b-c)|+2>|c-a|+1.
3.解法1C.如图1所示,设⊙O的半径为r,由相交弦定理和勾股定理,可得
24·18=AE·EB=(r+OE)(r-OE)=r2-OE2,
242=r2+OE2,
把它们相加后,可求得OE=62.
4.D.由x∈(0,1)知,在f(x)的解析式中可不妨设p,q∈N,p>q,(p,q)=1.
由f(x)>17,可得x=qp,f(x)=1p>17;p=2,3,4,5,6,进而可得
x=12,13,23,14,34,15,25,35,45,16,56
所以满足题设的x的个数为11.
5.A.解法1D.因为x4+ax2+bx+c=(x2-3x-1)(x2+3x+a+10)+(3a+b+33)x+a+c+10,所以由题意,得方程x2-3x-1=0的两个根3+132,3-132均是方程(3a+b+33)x+a+c+10=0的根,所以3a+b+33=a+c+10=0.得a+b-2c=(3a+b+33)-2(a+c+10)-13=-13.
解法2D.由题设,可得(x2-3x-1)(x4+ax2+bx+c).又注意到x4+ax2+bx+c不含x3项,所以x4+ax2+bx+c=(x2-3x-1)(x2+3x-c),x4+ax2+bx+c=x4-(c+10)x2+3(c-1)x+c.
8.B.因为实系数一元二次方程的两个虚数根是一对共轭复数,所以可设x1=r(cosθ+isinθ),x2=r[cos(-θ)+isin(-θ)](r>0).
得x21x2=r(cos3θ+isin3θ),
因为x21x2为实数,所以θ=kπ3(k∈Z),再得
x1x2=cos2kπ3+isin2kπ3≠1
x1x22016=cos2kπ3·2016+isin2kπ3·2016
=cos(2kπ·672)+isin(2kπ·672)=1,
所以∑2015k=0x1x2k=1-x1x220161-x1x2=0.
9.D.这是均匀分组问题,不同的分法种类为
C412C48C443!=5775.
10.A.如图3所示,由∠BAF=∠CAE,∠BAC=90°,得∠EAF=90°.
又因为∠BAD=∠ACD,所以AD⊥BC.得
DE·DF=AD2=BD·DC,
(5-2)(4+2)=2DC,
DC=9,
BC=BD+DC=2+9=11.
图3图411.B.如图4所示,设BK与小圆交于点M,连结ML,设CD为两圆在公共点K处的公切线.
由弦切角定理,得∠BAK=∠DKM=∠KLM.
又因为∠KLA=∠KML,所以∠AKL=∠BKL.
再由三角形角平分线性质,可得ALBL=AKBK,
可求得BL=25.
12.C.在题设所给的等式中分别令x=0,1,-1,
得2f(0)+f(-1)=1,
2f(1)+f(0)=1,
2f(-1)+f(0)=1,
可解得f(0)=f(1)=f(-1)=13.
再在题设所给的等式中令x=-2,得2f(-2)+f(1)=1,所以f(-2)=13.
图513.A.在图5所示的正9边形ABCDEFGHI中,以A为顶角的顶点的等腰三角形有且仅有4个(△ABI,△ACH,△ADG,△AEF),其中有且仅有△ADG是正三角形.
所以所求答案是3·9+93=30.
14.B.考虑a=mn,b=pq,c=mp,d=nq(m,n,p,q∈N*),得a+b+c+d=mn+pq+mp+nq=(m+q)(n+p),所以只要选a+b+c+d是合数即可.
而101,401都是质数,且301=7·43=(1+6)(1+42),
所以取m=1,q=6,n=1,p=42,得a=1,b=252,c=42,d=6,所以本题选B.
15.D.可设x3-3x2=y3-3y2=z3-3z2=m,得x,y,z是关于t的一元三次方程t3-3t2-m=0的三个实数根.
由韦达定理,得x+y+z=3.
16.解法1C.设f(x)=4x+1,得
f′(x)=24x+1,f″(x)=-4(4x+1)-32<0,

