“函数单调性”概念建构过程的教学反思与重构
蒋智东 戈晨曦
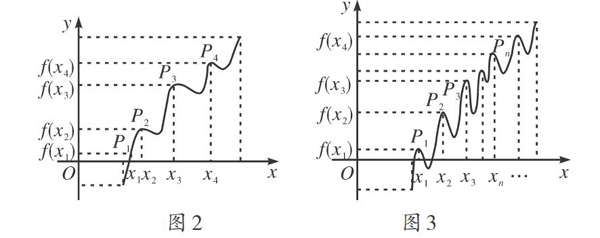
[摘要]函数的性质是函数知识的一个重要内容.所有函数性质学习活动本质是相同的,都是用抽象的代数式去刻画函数图像的几何特征函数单调性”是函数的核心概念,在教学中具有引领作用,教师应引起重视.
[关键词]函数单调性;教学;反思;重构
[中图分类号]G633.6? [文献标识码]A? [文章编号]1674-6058(2020)02-0001-03
函数的性质是函数知识的一个重要内容.在高中阶段,主要研究函数的单调性、奇偶性和周期性.所有函数性质的学习活动本质是相同的,都是用抽象的代数式去刻画函数图像的几何特征函数单调性”是苏教版教材中代数模块的一个核心概念,是函数性质中第一个引人的概念,在教学中具有引领作用.
一、教学现状与反思
在日常教学中,仍有许多教师为追求教学进度和所谓的课堂容量,在进行函数单调性教学时,快速引人函数单调性的概念,匆忙进入函数单调性的判断,并将学习的重点放在怎样判断函数在给定区间上的单调性上,然后基于若干个具体例子提炼函数单调性的判断步骤,最后用精练的语言进行概括,以方便学生记忆和运用.
也有相当一部分教师重视数学概念教学,重视概念教学中学生的概括、抽象等数学素养的培养.但是,由于对数学概念教学和“函数单调性”概念理解上的差异,使得概念教学还存在许多值得改进的地方.
其一,在“函数单调性”概念建构的初始阶段,学生需要通过实例来感悟函数图像的“上升”和“下降”,提取函数的图像特征.有的教师直接利用了教材上的“气温变化图”,难免有片面性.因为,函数图像的几何形态是多样的,在定义域上有上升的,有下降的,或在其定义域的某个区间上是上升的,在另一个区间上是下降的,等等.气温变化图中只是其中一种情形,由于来自具体实际,又显得过于复杂,这样会阻碍甚至不能帮助学生从几何直观的角度形成对函数单调性的比较全面的认识.这种缺失,会直接影响学生对函数单调区间的局域性以及单调区间与函数定义域之间的关系的认识和正确理解.
其二,有的教师直接由“气温变化图”出发引领学生经历函数单调性定义的形式化的形成过程,不符合学生的“认知规律气温变化图”实际上只是起到引入的作用.一是时间变化气温就变化,它是一个函数;二是这个函数图像有比较明显的升高或下降的趋势变化,便于学生观察并体会到这个特征.由于气温变化图与学生初中熟悉的函数图像相比,明显复杂得多,再加上缺少函数解析式,这种情况下,直接作为引例来探究函数单调性定义,可能会影响或弱化学生的探究意识和探究能力的培养.
其三,学生在初中阶段对函数单调性已经有了初步的认识,有的教师对高中阶段函数单调性为什么要从研究图像过渡到研究函数解析式,研究的必要性没有做出交代,缺少一个逻辑上的衔接.
其四,引导学生经历一个挣脱“无限”桎梏的过程是“函数单调性”概念建构的难点.许多教师仍是心有余而力不足.由于设计不恰当和引导不到位,对“增大”“随”“任意”等关键字、词还是做了正面的讲解与引导,给出了函数单调性符号化的描述,探究合作的成分不多.
二、在实践中重构教学
数学概念有其发生、发展、形成和应用的过程.在初中数学知识的基础上,学生对函数单调性的认识应有三个阶段.首先,借助函数图像的几何特征,从语言上对函数的单调性加以描述;其次,从图像过渡到解析式,由感性认识上升到理性认识;最后,完成归纳,抽象出函数单调性的符号化定义.
为使学生充分感受数学概念的发生与发展过程,经历观察、归纳、抽象的探究过程,加深對函数单调性的本质的认识,可以设计三个环节,引导学生分别完成对函数单调性定义的三次认识(本文重点谈前两次认识).
[教学设计]
在情境教学阶段,出示我市某天24小时内的气温变化图,引导学生识图,捕捉信息,启发学生思考.通过活动,让学生体会到函数值随自变量的变化而变化.
引言:对于自变量变化时,函数值是变大还是变小,是函数的重要性质,称为函数的单调性.同学们在初中对函数的这种性质就有了一定的认识,但是没有严格的定义.今天我们的首要任务就是建立函数单调性的严格定义.
1.借助图像,直观感知
本环节的教学主要是从学生的已有认知出发,即从学生熟悉的常见的函数图像出发,直观感知函数的单调性,完成对函数单调性定义的第一次认识.
问题1:分别作出函数y=x+2,y=-x+2,y=x2以及y=1/x的图像,并且观察自变量变化时,函数值有什么变化规律?
在学生画图的基础上,引导学生观察图像,获得信息:第一个图像从左向右逐渐上升,y随x的增大而增大;第二个图像从左向右逐渐下降,y随x的增大而减小.然后让学生明确,自变量变化时,函数值具有这两种变化规律的函数,我们分别称为增函数和减函数.
对两个函数图像的上升与下降要分段说明.通过讨论,使学生明确函数的单调性是对定义域内某个区间而言的,是函数的局部性质.
对于概念教学,若学生能用自己的语言来表述概念的相关属性,则能更好地理解和掌握概念.
问题2:能否根据自己的理解说说什么是增函数,什么是减函数.
引导学生进行分类描述(增函数、减函数),并用自己的语言描述增函数的定义:
如果函数f(x)在某个区间上的图像从左向右逐渐上升,或者如果函数f(x)在某个区间上随自变量x的增大,y也越来越大,我们就说函数f(x)在该区间上为
增函数.
然后让学生类比描述减函数的定义.至此,学生对函数单调性就有了一个直观、描述性的认识.
2.探究规律,理性认识
在此环节中,可以设计两个问题,通过对两个问题的研究、交流、讨论,将函数的单调性研究从研究函数图像过渡到研究函数的解析式,使学生对单调性的认识由感性认识上升到理性认识,完成对概念的第二次认识.
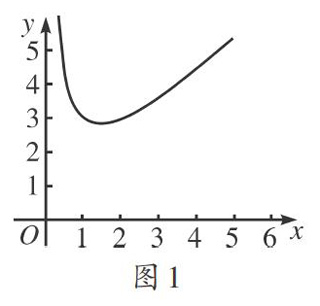
问题3:图1是函数y=x+(2/x)(x>0)的图像,能说出这个函数分别在哪个区间为增函数和减函数吗?
学生解决问题所遇到的困难是难以确定分界点的确切位置.通过讨论,使学生感受到用函数图像判断函数单调性虽然比较直观,但有时不够精确,需要结合解析式进行严密化、精确化的研究;使学生体会到用数量大小关系严格表述函数单调性的必要性,从而将函数的单调性研究从研究函数图像过渡到研究函数的解析式.
问题4:如何从解析式的角度说明f(x)=x2在[0,+∞)上为增函数?
在前面问题的铺垫下,问题4是形成函数单调性概念的关键.在教学中,教师可组织学生先分组探究,然后全班交流,相互补充,并及时对学生的发言进行反馈、评价,对于普遍出现的问题组织学生讨论,使学生在辨析中达成共识.
[课堂实录]
生1:只需用数学式子来描述:“在区间[0,+∞)上,当自变量x增大时,函数值f(x)随之增大.”
生2:“增大”意味着比较,需要建立两个量的大小关系.
师:好!那应该怎样表示呢?
生3:在区间[0,+∞)内取两个数,比如2和3,因为2<3,且f(2)=4

