多成分悬链式锚泊线静态特性分析

    杨万昌　潘沈浩

    

    

    

    摘要：本文以悬链式锚泊线的相关理论编写了相应的单根锚泊线静态特性分析程序，并通过水动力软件sesaln验证了程序的准确性。在此基础上以一根作用于600m水深的锚泊线为例，研究预张力倾角、水流流速以及上端点运动等对锚泊线形状和顶张力的影响，得到了一些有意义的结论，可以为将来锚泊系统的初步设计提供一些参考。

    关键词：悬链线；分段外推法；顶张力；系泊系统

    中图分类号：U675.92 文献标识码：A 文章编号：1006-7973（2016）03-0036-02

    研究单根锚泊线的特性是分析整个系泊系统的基础。传统的锚泊线分析方法是采用悬链线理论来分析其受力特性，但悬链线方程忽略了海流力作用和锚泊线的弹性拉伸。本文在考虑海流作用和锚泊线弹性伸长的影响下，从锚泊线预张力倾角、海流流速以及上端点运动三个方面人手研究了单根锚泊线的静态特性。本文的分析结果可以为系泊系统的初步设计提供依据，也可以作为动力分析的基础。

    1锚泊线的静态特性分析

    1.1单根锚泊线的静力分析

    文献对锚泊线的静态特性进行了研究。本文主要采用文献中介绍的方法，任取一根锚泊线，从上而下划分为n个单元，取其第i段进行受力分析，外荷载全部集中在单元中心上，作用于单元中心的外力有水流力和重力。如图1所示，其中锚泊线底部与海底相切。

    由静力平衡方程忽略二阶无穷小量后得到：

    （1）

    （2）

    式中：T、P分别为锚链的张力和浮容重；D、F分别为单位长度上锚链受到的法向和切向海流力；θ为张力T与水平方向的夹角；ds、dT、dθ分别为微段长度、拉力增量和角度增量；ε为锚链单位长度的弹性伸长量。

    根据式（1）和（2）得到单元i上的平衡方程：

    （3）

    （4）

    （5）

    根据微段的几何关系可得到单元节点坐标的空间关系：

    （6）

    （7）

    1.2方程求解

    上端点与海底系泊点位置的竖直高度记为H，求解过程采用迭代方法，计算过程如下：

    （1）假设一个锚泊线顶端和水平方向的夹角为；

    （2）把不均匀锚链分别划分成若干个单元，将每个单元上的重力和水流力都简化到单元的中心上；

    （3）把前一段锚链的末端点作为下一段锚链的起点；

    （4）在给定的预张力下求解方程，可得到水平跨距、垂直跨距、顶端张力以及水平回复力等；

    （5）验证边界条件：Y=H，若满足边界条件，则停止计算，若不满足则返回（1）重新进行迭代求解，直到满足一定精度为止。

    1.3程序验证

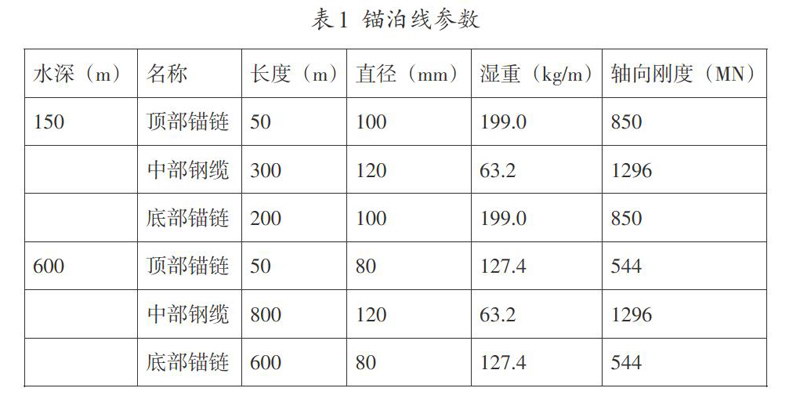
    根据上述步骤编写了相应的单根锚泊线静态特性分析程序。为了验证程序编写的准确性，现对一根150m水深的多成分锚泊线进行静态特性分析，并与水动力软件Sesam的计算结果进行对比，锚泊线参数如表1所示，静态特性曲线如图2所示。

    由图2可看出本程序的计算结果与水动力软件Sesam的计算结果吻合良好，说明本文所编写的程序是准确可靠的，可用于后续计算分析。

    2算例分析

    以一根用于600m水深的多成分锚泊线为研究对象进行分析，具体参数如表1所示。本文以锚泊线与海底相切为前提，进行了上端点最小预张力倾角的计算，临界预张力倾角随海流流速的变化曲线如图3所示。从图中可以看出随着海流速度的不断增大，海流对预张力倾角的影响也逐渐变大。对于海流较大的海域而言，海流的作用不容忽视。

    2.1不同预张力倾角下的锚泊线形状

    由图3插值得到海流速度V=0m/s时的临界预张力倾角为40.54°，在大于临界值条件下给定不同的预张力倾角，相应的锚泊线曲线如图4所示，预张力随倾角的变化曲线如图5所示。

    从图4中可以看出预张力倾角越大，拖地段锚链长度增大，水平跨距减小。从图5中可以看出预张力倾角越大，锚泊线预张力越小，抵抗平台运动的能力便会减弱，所以在做系泊设计时可根据需要选择合适的预张力倾角。

    2.2不同流速下的锚泊线形状

    计算海流速度V=0m/s、V=0.5nd s、V=lm/s时的锚泊线形状曲线，由图3插值得到临界预张力倾角分别为：40.54°、40.87°、42°，在大于临界值条件下给定无流速时预张力倾角45°，不同流速下的锚泊线形状如图6所示。从中可以看出海流流速对锚泊线的形状有一定影响，流速越大，拖地段锚链长度越小，悬挂在水中的锚链长度变大，预张力倾角变大。

    2.3上端点运动对锚泊线的影响分析

    给定锚泊线上端点位移时程曲线x=20*sin（z/25*t），所有状态下初始预张力均取1000KN，相应的张力时程曲线如图7所示，不同流速下的锚泊线顶张力时程曲线如图8所示。

    从图7中可以看出上端点顶张力、水平回复力和垂向回复力与位移时程曲线基本一致，呈现正弦变化规律，水平回复力受位移的影响较垂向回复力更大一些。从图8中可以看出在初始预张力不变的情况下，海流流速对上端点运动周期没有影响。随着海流流速的增加，顶张力在波峰和波谷处的幅值有所减小，使得具有相同位移的上端点在海流速度较大时拥有较小的顶张力。

    3結束语

    本文在考虑海流力作用和锚泊线弹性伸长的影响下，推导了单根锚泊线的迭代方程，并以此为基础编写了相应的锚泊线静态特性分析程序，并用Sesam软件对其进行验证，结果证明本文程序是准确可靠的。通过分析可以得到以下结论：锚链长度与水深一定时，预张力与预张力倾角呈负相关；海流流速可改变锚泊线的形状，流速越大，悬挂在水中的锚链长度和预张力倾角也越大；在初始预张力不变的情况下，海流流速对上端点运动周期没有影响，具有相同位移的上端点在海流速度较大时拥有较小的顶张力。