平均数、中位数和众数的应用思考
范江城??
【摘要】从平均数、众数和中位数学习和应用中遇到的困惑出发,比较分析了平均数、众数和中位数的内涵、数量关系和应用中需要注意的主要方面,坚信以不唯书、不唯上的科学态度对待学习,以更好地解决社会生活中的实际问题.
【关键词】平均数;中位数;众数;应用
目前,平均数、众数和中位数在中学和大学中都要学习,并且在实际生活中应用非常广泛,但是,在学习和应用过程中还存在一些有争议的问题.本文将从平均数、众数和中位数三者的内涵比较、数量关系和应用问题进行分析,以期促进学习时多思考、多参阅文献,真正掌握所学知识,并更好地应用于实践中.
1平均数、中位数和众数的内涵比较
平均数、中位数和众数都是反映一组数据集中趋势特征的数值.其中,平均数分为广义平均数和狭义平均数,广义的平均数分为数值平均数和位置平均数,数值平均数包括算术平均数、调和平均数、几何平均数,这些平均数都是根据同一现象数据来计算,用以反映现象在具体条件下一般水平、集中趋势.位置平均数包括中位数和众数,主要根据现象数据在一定位置确定现象集中趋势的数据.本论文所研究的平均数是指狭义的平均数,即算术平均数,在本论文后面部分的如不加特别注明都指算术平均数.狭义平均数是现象中的所有个体的某一数据总和除以个体总数而计算的平均数.在实际生活中用得最为广泛,如班级平均成绩、平均身高、平均年龄,企业员工的平均工资等.
在理解平均数内涵时,要注意同一现象和包含的个体数据,如果不是同一现象或者计算的个体数不是计算现象的个体数,就不能理解为平均数.举个例子说明:人均粮食产量和人均粮食消耗量,这两个数据看上去很相似,并且都有人均,其实只有人均粮食消耗量是平均数,而人均粮食产量不是平均数.如2015年全国粮食总产量为124287亿斤、全国粮食消耗总量为348758亿斤、中国总人口数量为136782亿人,那么计算人均粮食产量时用124287亿斤除以136782亿人等于90866斤/人,在人均粮食产量中的总人数136782亿人中包含了没有生产粮食的在校学生等,所以人均粮食产量从形式上看是平均数,其实它没有平均数的内涵,不能作为平均数.计算人均粮食消耗量时用348758亿斤除以136782亿人等于2549斤/人,因为不管是大人还是小孩,每个人都要消费粮食,也就是2015年中国总人口数量为136782亿的人们消耗了粮食总量为348758亿斤,对人们消耗粮食这个现象来说,包含了所有的人们个体数,所以,人均粮食消耗量具有平均数的内涵,它是一个平均数.
中位数是指某一现象中某一数据按大小顺序排列、居于中间位置的那个数据.如某中学1班有51名同学,一次考试中,按某科成绩从小到大依次排列,排在中间的学生成绩是85分,那么如果用中位数来反映1班全体同学的平均成绩就是85分;又如2班有50名同学,这时排在中间位置就有两名同学,确定2班同学的成绩中位数时就用中间两名同学成绩的算术平均数来反映.
众数是指某现象中出现次数最多的那个数据就是众数.在一个现象中可能有众数,也可能没有众数,最典型的就是如果这一现象所有数据都一样大小,没有哪个数据出现的次数比其他数据多,这时就无法确定众数.所以,只有在现象的数据个数比较多,而且又有某一个或多个出现的次数明显比其他数据多时才存在众数,并且众数不像算术平均数和中位数,它可以有多个,若有多个数据出现次数相等的众数就称为复众数.
2平均数、中位数和众数的数量关系
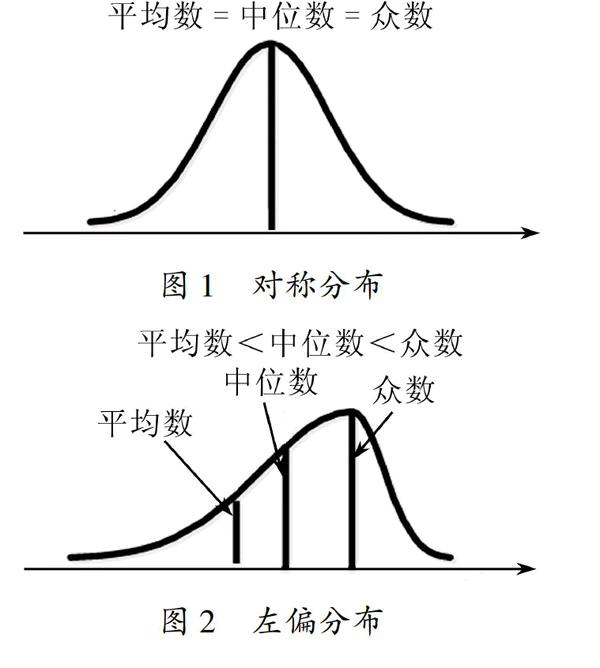
关于算术平均数、中位数和众数之间的数量关系,大多数教材上的观点认为这三者之间的数量关系与总体的分布特征有关:(1)现象数据呈无偏分布时,算术平均数、中位数和众数相等(见图1);(2)现象数据呈左偏分布时,平均数小于中位数,中位数小于众数(见图2);(3)现象数据呈右偏分布时,众数小于中位数,中位数小于平均数(见图3).
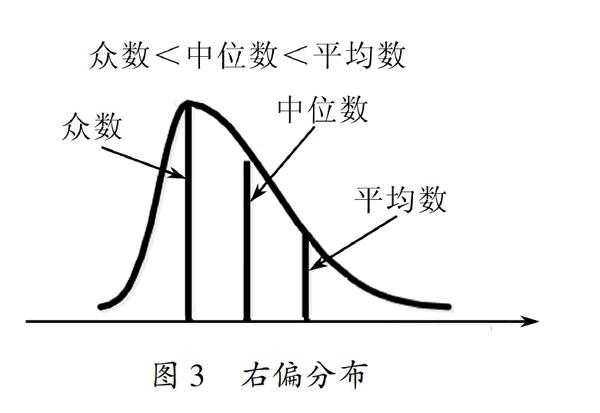
图1对称分布图2左偏分布图3右偏分布江海峰(2007)从不同变量类型和偏度下抽取数据分析了平均数、中位数和众数之间的数量关系,指出了现行教材关于三者关系的结论存在的问题[1].他认为当现象数据无偏分布时,始终存在平均数、中位数和众数相等.当现象数据呈左偏分布时,在离散型分布情况下,并不是平均数始终小于中位数,中位数始终小于众数,还有众数和中位数相等并且大于平均数,也有众数、中位数和平均数三者相等情况,可见,当现象数据呈左偏分布时,还有平均数<中位数<众数以外情形,大多教材上的观点不够全面.当现象数据呈右偏分布时,在离散型分布下,存在平均数等于中位数且大于众数情况,还存在平均数、中位数、众数三者相等情况.可见,当现象数据呈右偏分布时,还有众数<中位数<平均数以外情形,教材上的观点也不够全面.
3平均数、中位数和众数的应用问题
平均数、中位数和众数反映了一组数据的平均值的大小,常用来代表一组数据的“一般水平”.在实际应用中,可以进行同类现象在不同空间、不同时间上的对比,可以分析现象之间的依存关系,也可以作为论断事物的一种数量标准或参考,但是当数据中有“异常数”时,通常会出现不能科学反映现象本质[2].
平均数是现象数据的代表值,在实际生活中应用非常广泛,在应用中要注意是否有实际意义.1831年,魁特奈特(A.Quetelet,1796—1874)提出了“平均人”的概念,他认为“平均人”是在重要指标上都具有某群体中一切个体相应指标的平均值的人,“平均人”实际生活中是不存在的[3].又如对“平均每个家庭有27个人”,显然人也不可能是07个人.如一句顺口溜就说明了平均数存在的问题:“有个暴富张千万,邻居九个穷光蛋,专家统计平均数,都是张百万”.另外一个典型例子,如果某班有50名同学,前25名同学考试成绩都在80分以上,而后25名同学考试成绩都在60分以下,如果计算平均数出的平均成绩为70分,这时的平均数70分也没有实际意义,根本没有同学是70分或集中在70分左右.显然,这些平均数,根本不能反映实际情况,完全失去了实际意义.所以,计算平均数存在实际意义,现象没有异常数据,并且分布比较均衡,适宜使用平均数来代表现象集中趋势[4].在现象的数据比较均匀分布时,平均数能比较科学地反映现象本质特征,平均数的代表性比较强,理解也容易,才有足够说服力.
中位数总体来说,因为它只利用了现象中个别数据来确定集中趋势,代表性和可靠性都比较差.一般情况下,现象存在极大或极小值等异常数据时,才用中位数来描述现象的规律和特征.如前面提到的“暴富张千万”的例子,如果用中位数来反映他们的收入就比较科学合理了,而不是大多集中在百万元收入,也不会让人们难以理解.再比如大家关心的住房现象,如果某人有几十套、甚至几百套房产,并且都是大面积房产,在一定范围内如果用平均数来反映居民的住房面积,就不能够真实地反映现象本质,这时应用中位数却能比较好地反映人们的居住面积.在应用中位数时,我们还需要注意另外一个问题,首先对给定现象的数据按从小到大或者从大到小进行排序后,处在中间位置的那个数(奇数个数时)或处在中间位置的那两个数(偶数个数时)的算术平均数,而不是直接找到数据中间位置的数,因为当一个现象的数据随便编排时,处于中间的数是发生变化的,只有将现象数据按大小顺序排序后,中间位置的数才是确定的,也就确定了一个现象的中位数.
众数作为现象数据的代表时,也只用了个别数据来反映现象集中趋势,可靠性也比较差.在现象的数据中如果存在异常数据,为了去除这些异常数据的影响,用出现次数最多的数据来反映现象的集中趋势,是比较科学合理的.在实际生活中,众数通常应用在不确定情况下或为了省时省力而对结果影响不大的情况下.例如,农贸市场每天菜农卖的蔬菜价格、商场中销售的衣服的尺寸、鞋的尺寸等等是根据众数来确定的.这些数据的代表性如果用平均数来反映,几乎是不可能的,也没必要,应用众数就更具有现实意义.
总之,平均数、中位数和众数仍然在实际生活中广泛应用,但是在应用时一定要结合现象的具体情况来分析.社会经济现象有“橄榄球”型、“哑铃”型、“J”型和“反J”型等,有的现象的数据是不适合用平均数、中位数和众数来反映其本质特征的,就可以分成不同阶段、考虑权重进行分析,并结合极差、方差、标准差等手段进行比较研究,才能更好地揭示现象的本质规律,更好地发挥平均数、中位数和众数在实际生活中的作用.
参考文献
[1]江海峰.算术平均数、众数、中位数之间关系的再探讨[J].统计教育,2007(10):37-39.
[2]范召霞.帮你分辨平均数、众数、中位数[J].初中生辅导,2012(72):35-39.
[3]吴骏,黄青云.基于数学史的平均数、中位数和众数的理解[J].数学通报,2013(11):16-21.
[4]唐芳.算术平均数、众数、中位数的合理运用[J].中国统计,2008(3):49-50
【摘要】从平均数、众数和中位数学习和应用中遇到的困惑出发,比较分析了平均数、众数和中位数的内涵、数量关系和应用中需要注意的主要方面,坚信以不唯书、不唯上的科学态度对待学习,以更好地解决社会生活中的实际问题.
【关键词】平均数;中位数;众数;应用
目前,平均数、众数和中位数在中学和大学中都要学习,并且在实际生活中应用非常广泛,但是,在学习和应用过程中还存在一些有争议的问题.本文将从平均数、众数和中位数三者的内涵比较、数量关系和应用问题进行分析,以期促进学习时多思考、多参阅文献,真正掌握所学知识,并更好地应用于实践中.
1平均数、中位数和众数的内涵比较
平均数、中位数和众数都是反映一组数据集中趋势特征的数值.其中,平均数分为广义平均数和狭义平均数,广义的平均数分为数值平均数和位置平均数,数值平均数包括算术平均数、调和平均数、几何平均数,这些平均数都是根据同一现象数据来计算,用以反映现象在具体条件下一般水平、集中趋势.位置平均数包括中位数和众数,主要根据现象数据在一定位置确定现象集中趋势的数据.本论文所研究的平均数是指狭义的平均数,即算术平均数,在本论文后面部分的如不加特别注明都指算术平均数.狭义平均数是现象中的所有个体的某一数据总和除以个体总数而计算的平均数.在实际生活中用得最为广泛,如班级平均成绩、平均身高、平均年龄,企业员工的平均工资等.
在理解平均数内涵时,要注意同一现象和包含的个体数据,如果不是同一现象或者计算的个体数不是计算现象的个体数,就不能理解为平均数.举个例子说明:人均粮食产量和人均粮食消耗量,这两个数据看上去很相似,并且都有人均,其实只有人均粮食消耗量是平均数,而人均粮食产量不是平均数.如2015年全国粮食总产量为124287亿斤、全国粮食消耗总量为348758亿斤、中国总人口数量为136782亿人,那么计算人均粮食产量时用124287亿斤除以136782亿人等于90866斤/人,在人均粮食产量中的总人数136782亿人中包含了没有生产粮食的在校学生等,所以人均粮食产量从形式上看是平均数,其实它没有平均数的内涵,不能作为平均数.计算人均粮食消耗量时用348758亿斤除以136782亿人等于2549斤/人,因为不管是大人还是小孩,每个人都要消费粮食,也就是2015年中国总人口数量为136782亿的人们消耗了粮食总量为348758亿斤,对人们消耗粮食这个现象来说,包含了所有的人们个体数,所以,人均粮食消耗量具有平均数的内涵,它是一个平均数.
中位数是指某一现象中某一数据按大小顺序排列、居于中间位置的那个数据.如某中学1班有51名同学,一次考试中,按某科成绩从小到大依次排列,排在中间的学生成绩是85分,那么如果用中位数来反映1班全体同学的平均成绩就是85分;又如2班有50名同学,这时排在中间位置就有两名同学,确定2班同学的成绩中位数时就用中间两名同学成绩的算术平均数来反映.
众数是指某现象中出现次数最多的那个数据就是众数.在一个现象中可能有众数,也可能没有众数,最典型的就是如果这一现象所有数据都一样大小,没有哪个数据出现的次数比其他数据多,这时就无法确定众数.所以,只有在现象的数据个数比较多,而且又有某一个或多个出现的次数明显比其他数据多时才存在众数,并且众数不像算术平均数和中位数,它可以有多个,若有多个数据出现次数相等的众数就称为复众数.
2平均数、中位数和众数的数量关系
关于算术平均数、中位数和众数之间的数量关系,大多数教材上的观点认为这三者之间的数量关系与总体的分布特征有关:(1)现象数据呈无偏分布时,算术平均数、中位数和众数相等(见图1);(2)现象数据呈左偏分布时,平均数小于中位数,中位数小于众数(见图2);(3)现象数据呈右偏分布时,众数小于中位数,中位数小于平均数(见图3).

图1对称分布图2左偏分布图3右偏分布江海峰(2007)从不同变量类型和偏度下抽取数据分析了平均数、中位数和众数之间的数量关系,指出了现行教材关于三者关系的结论存在的问题[1].他认为当现象数据无偏分布时,始终存在平均数、中位数和众数相等.当现象数据呈左偏分布时,在离散型分布情况下,并不是平均数始终小于中位数,中位数始终小于众数,还有众数和中位数相等并且大于平均数,也有众数、中位数和平均数三者相等情况,可见,当现象数据呈左偏分布时,还有平均数<中位数<众数以外情形,大多教材上的观点不够全面.当现象数据呈右偏分布时,在离散型分布下,存在平均数等于中位数且大于众数情况,还存在平均数、中位数、众数三者相等情况.可见,当现象数据呈右偏分布时,还有众数<中位数<平均数以外情形,教材上的观点也不够全面.

3平均数、中位数和众数的应用问题
平均数、中位数和众数反映了一组数据的平均值的大小,常用来代表一组数据的“一般水平”.在实际应用中,可以进行同类现象在不同空间、不同时间上的对比,可以分析现象之间的依存关系,也可以作为论断事物的一种数量标准或参考,但是当数据中有“异常数”时,通常会出现不能科学反映现象本质[2].
平均数是现象数据的代表值,在实际生活中应用非常广泛,在应用中要注意是否有实际意义.1831年,魁特奈特(A.Quetelet,1796—1874)提出了“平均人”的概念,他认为“平均人”是在重要指标上都具有某群体中一切个体相应指标的平均值的人,“平均人”实际生活中是不存在的[3].又如对“平均每个家庭有27个人”,显然人也不可能是07个人.如一句顺口溜就说明了平均数存在的问题:“有个暴富张千万,邻居九个穷光蛋,专家统计平均数,都是张百万”.另外一个典型例子,如果某班有50名同学,前25名同学考试成绩都在80分以上,而后25名同学考试成绩都在60分以下,如果计算平均数出的平均成绩为70分,这时的平均数70分也没有实际意义,根本没有同学是70分或集中在70分左右.显然,这些平均数,根本不能反映实际情况,完全失去了实际意义.所以,计算平均数存在实际意义,现象没有异常数据,并且分布比较均衡,适宜使用平均数来代表现象集中趋势[4].在现象的数据比较均匀分布时,平均数能比较科学地反映现象本质特征,平均数的代表性比较强,理解也容易,才有足够说服力.
中位数总体来说,因为它只利用了现象中个别数据来确定集中趋势,代表性和可靠性都比较差.一般情况下,现象存在极大或极小值等异常数据时,才用中位数来描述现象的规律和特征.如前面提到的“暴富张千万”的例子,如果用中位数来反映他们的收入就比较科学合理了,而不是大多集中在百万元收入,也不会让人们难以理解.再比如大家关心的住房现象,如果某人有几十套、甚至几百套房产,并且都是大面积房产,在一定范围内如果用平均数来反映居民的住房面积,就不能够真实地反映现象本质,这时应用中位数却能比较好地反映人们的居住面积.在应用中位数时,我们还需要注意另外一个问题,首先对给定现象的数据按从小到大或者从大到小进行排序后,处在中间位置的那个数(奇数个数时)或处在中间位置的那两个数(偶数个数时)的算术平均数,而不是直接找到数据中间位置的数,因为当一个现象的数据随便编排时,处于中间的数是发生变化的,只有将现象数据按大小顺序排序后,中间位置的数才是确定的,也就确定了一个现象的中位数.
众数作为现象数据的代表时,也只用了个别数据来反映现象集中趋势,可靠性也比较差.在现象的数据中如果存在异常数据,为了去除这些异常数据的影响,用出现次数最多的数据来反映现象的集中趋势,是比较科学合理的.在实际生活中,众数通常应用在不确定情况下或为了省时省力而对结果影响不大的情况下.例如,农贸市场每天菜农卖的蔬菜价格、商场中销售的衣服的尺寸、鞋的尺寸等等是根据众数来确定的.这些数据的代表性如果用平均数来反映,几乎是不可能的,也没必要,应用众数就更具有现实意义.
总之,平均数、中位数和众数仍然在实际生活中广泛应用,但是在应用时一定要结合现象的具体情况来分析.社会经济现象有“橄榄球”型、“哑铃”型、“J”型和“反J”型等,有的现象的数据是不适合用平均数、中位数和众数来反映其本质特征的,就可以分成不同阶段、考虑权重进行分析,并结合极差、方差、标准差等手段进行比较研究,才能更好地揭示现象的本质规律,更好地发挥平均数、中位数和众数在实际生活中的作用.
参考文献
[1]江海峰.算术平均数、众数、中位数之间关系的再探讨[J].统计教育,2007(10):37-39.
[2]范召霞.帮你分辨平均数、众数、中位数[J].初中生辅导,2012(72):35-39.
[3]吴骏,黄青云.基于数学史的平均数、中位数和众数的理解[J].数学通报,2013(11):16-21.
[4]唐芳.算术平均数、众数、中位数的合理运用[J].中国统计,2008(3):49-50

