指向计算思维培养的模型化思维教学模式实践
卢华 邓彰超
随着信息化的快速发展,信息素养已和人文素养、科学素养一样,成为现代人必须具备的核心素养。《普通高中信息技术课程标准(2017年版)》明确指出信息技术教学是培养学生信息技术学科核心素养的基本途径,并强调计算思维是信息技术核心素养的主要组成部分。“数据与数据结构”模块是新课程改革信息技术选考的必选模块,也是选考算法教学的重点,其知识体系抽象而繁杂(包含数组与链表、字符串、队列和栈、二叉树等),学习难度大。新课标要求学生针对限定条件的实际问题进行数据抽象,合理组织、存储数据,选择合适的算法编程实现,解决问题。这就需要学生在内化知识和实践解决问题的过程中运用计算机科学领域的思想方法形成问题的解决方案,即发展计算思维。而在选考数据与数据结构相关内容教学中,采用何种教学模式才能有效地培养和提升学生计算思维是一个值得关注和研究的问题。
● 模型化思维教学模式
1.模型化思维教学的模式探索
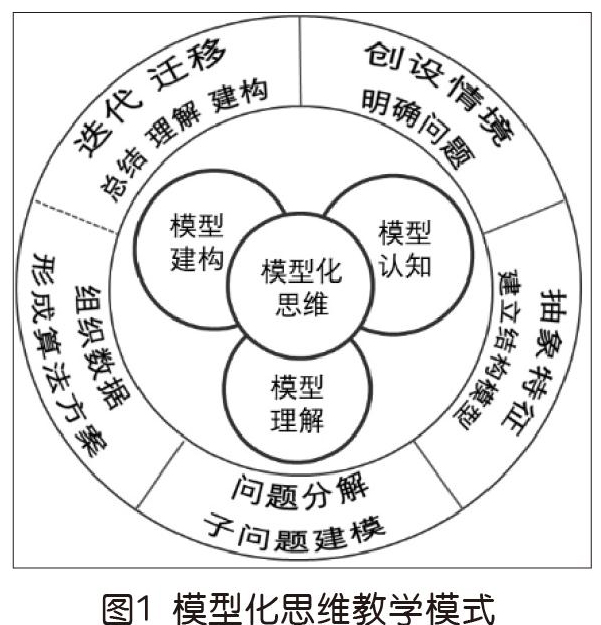
通过理论研究并结合教学实际,本研究以培养学生的计算思维能力为导向,尝试采用模型化思维手段,提出模型化思维教学模式,如图1所示。
该教学模式由内而外分两层构成,内层为指向计算思维培养的模型化思维教学方法,外层为选考数据与数据结构教学过程,二者有机融为一体。模型化思维运用于教学过程主要分三个阶段:①针对实际问题情境模型,通过直观认知等方式深化对概念的理解,明确问题,抽象问题特征,建立结构模型,培养学生抽象问题的能力;②通过对模型的深入理解,类比推演,抽象出问题规律特征,并进行子问题形式化分解建模,再通过对子问题模型的深入理解,抽象出子问题特征,并组织数据形成子问题算法方案,然后归结形成整个问题的解,以此来培养学生的抽象思维、分解思维、算法思维能力;③将问题解决中归纳建构生成的新知思维模型迭代迁移运用到其他类似问题解决中,培养并提升学生的概括、迁移思维能力。
2.模型化思维教学模式的教学流程
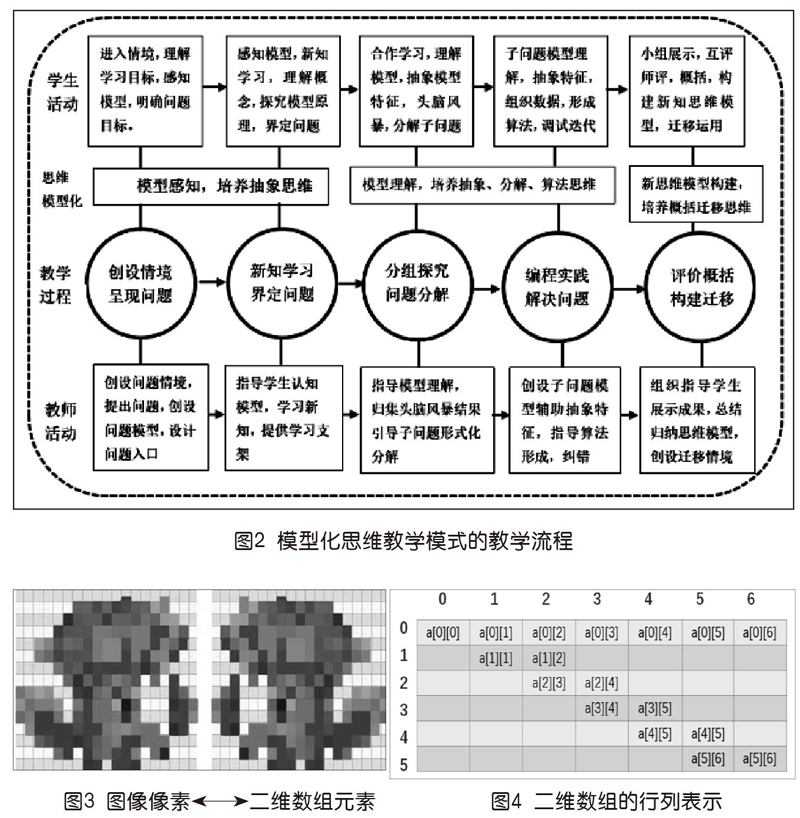
为了凸显模型化思维教学模式的教育蕴意及应用价值,本研究从教学过程、学生活动、教师活动三个角度出发,以培养学生的计算思维为目标,以计算思维的五个元素“明确问题”“抽象特征”“问题分解”“形成算法”“概括迁移”为切入点,融入“模型认知”“模型理解”“模型建构”的模型化思维方法,将模型化思维教学模式进一步细化为教学活动流程(如图2)。
● 模型化思维教学模式的实践探索
1.模型认知,培养抽象思维
通过对模型直观形象的认知,学生可以运用建构和研究模型的方法来把握复杂的、难以处理的事物,更容易抽象出事物的本质。以选考模块“数据与数据结构”中的二维数组及其应用为例,学生在初中阶段学习过Photoshop相关操作,故教师在问题创设情境、呈现问题环节引入平面图像处理项目,如图像的翻转、灰度化等,激发学生学习的兴趣。根据该项目情境模型,引导学生思考计算机内部如何处理该类问题,进一步引导学生思考平面图像相关操作背后蕴含的原理,并提出本项目学习的目标:小组合作,对平面图像通过编程进行全图灰度化、部分图像灰度化、全图翻转、镜像等变换操作,要求各小组提交实验作品及源程序。
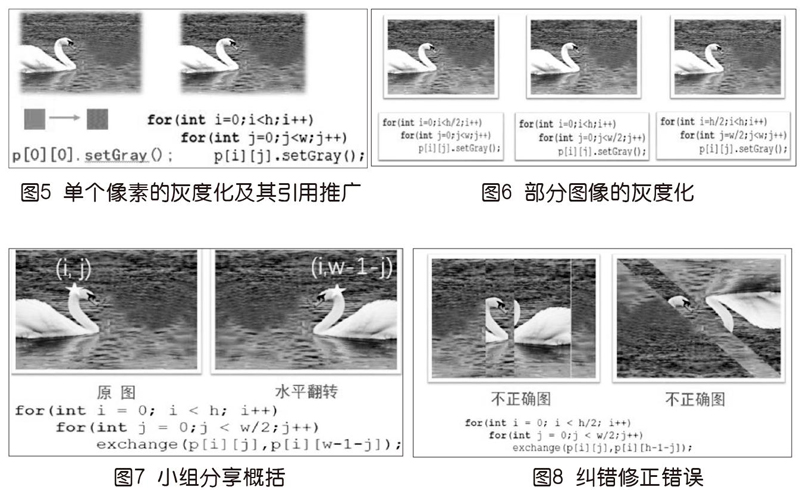
基于学生对位图像素的前置知识,教师在新知学习、界定问题环节,将数字化图像予以放大,创设出图像像素和二维数组元素之间的关系模型,并给出翻转后的图像,该模型创设能让学生直观感知到平面图像的翻转变化就是像素的对应变化(如图3)。接着在放大的位图中,鼠标选中哪个像素,该像素所在的坐标即行列位置就显示出来,抽象出数字图像与二维数组的对应关系,学生根据数字化位图坐标模型的进一步直观演示,认知模型,抽象出二维数组的行列坐标表示(如图4)。通过模型的直观认知学习,学生理解了二维数组的概念,界定出问题目标即对二维数组元素进行相关操作,抽象思维得到提升。
在数据与数据结构课程的其他内容的情境导入、新知学习中,也可采用模型认知的方式,辅助学生加深对概念的理解,并类比推理,探索模型背后的原理。
2.模型理解,培养抽象思维、分解思维、算法思维
明确平面图像处理项目即对相应二维数组元素进行某种操作后,教师组织学生进行小组合作,通过头脑风暴,归纳出项目的三个子问题:①对单个固定像素如何进行引用和相关操作;②像素区域如何引用,即二维数组如何引用遍历;③二维数组的相关操作应用。针对三个子问题,教师设置了三个探究活动。
活动一为单个像素的灰度化,学生在教师讲授、模型演示时,理解模型,抽象出单个像素的引用及其相关操作(如灰度化)的形式表达,随后教师引导学生利用枚举算法模型将元素的引用推广到二维数组(如图5)。
活动二是部分图像的灰度化,学生根据小组任务的相关要求,基于模型理解,抽象出部分图像的區域坐标,即明确枚举的范围,进而完成相关操作的编程实现。本活动中,学生在活动一模型理解的基础上,进一步掌握二维数组的引用和遍历(如图6)。
活动三是分组探究图像的翻转、镜像变换。学生基于模型理解,抽象出图像翻转的坐标位置关系,灵活应用二维数组的引用和遍历并进行相关操作,教师指导、纠错。至此,学生亲历问题的分解,并用二维数组结合程序实现,解决问题,其抽象思维能力、问题分解能力、算法思维能力得到提升。
3.建构新知思维模型,培养概括迁移思维
根据本项目的目标及其事先明确的评价标准,教师组织小组进行成果分享,包含效果图及源程序编程思路阐述,如水平翻转的规律是什么,对应像素是如何变换的(如图7),同时进行组间互评和师评。此时,可能会有错误效果图及错误的源程序(如图8),抓住这些错误点,师生共同探讨予以纠正,总结概括,更有利于构建生成正确的新知思维模型,并迁移运用。在尝试—验证—修正的试错纠错环节中,学生的概括思维、迁移思维得到培养提升。
至此,通过模型认知、模型理解,生成构建出新思维模型,扩展了知识网络。例如,在一维数组的基础上,通过平面图像处理模型,构建了二维数组思维模型,并可将其迁移运用到诸如影院订座、车位自动搜寻、在线围棋对弈等情境问题中。
● 模型化思维教学模式的研究成效
为了验证模型化思维教学模式对高中学生计算思维发展的成效,本研究根据吕宁等人提出的高中计算思维发展测量表,结合教学实际及新课标对学生计算思维发展要求,设计了《高中生计算思维发展情况调查》问卷,调查学生对模型化思维教学的满意情况。
1.问卷的编制
问卷依托计算思维的六个要素——明确问题、抽象问题、分解问题、解决问题、新知建构、概括迁移,并围绕计算思维的外显行为指标来编制。共设置6道题,以此检验学生计算思维的提升发展情况,如下页表1所示。问卷题项采用李克特五等级量表,选项按符合程度分为非常不满意、不满意、一般、满意、非常满意,分别在开展模型化思维教学模式前后进行实验调查。
2.问卷的信度和效度
为了验证调查问卷的信度和效度,本研究选取高二年级两个班共86名学生实施预测试,使用Spass22.0软件对调查问卷的内部一致性及相关结构效度进行分析。在信度检验中,Cronbachα系数为0.946,大于0.8,表明此调查量表各维度有较高的内部一致性,信度较好;在效度检测方面,KMO值为0.842,大于0.8,Bartlett球形检定P值为0.0002,小于0.001,结合两个数值结果,可见调查问卷具有较好的效度。
3.调查结果分析
本研究选取高二年级86位学生验证学习效果,分别在开展模型化思维教学模式前后通过问卷星发放调查问卷。86名学生全部填写,回收有效问卷86份,回收率100%。问卷调查结果如表1所示。
将问卷调查前测和后测得分率导入Spass22.0进行配对样本T检验,结果如表2所示,显著性(双尾)sig.=0.01,小于0.05,显示前测后测效果差异显著,说明基于模型化思维教学模式能有效提升学生的计算思维能力。
● 结论与思考
本研究借助模型化思维手段开展教学研究,以培养学生的计算思维为目标,总结和提出模型认知(培养抽象思维)、模型理解(培养抽象思维)分解思维及算法思维;模型建构(培养概括迁移思维的模型化思维)教学模式,并在高二“数据与数据结构”模块的相关内容(如字符串、数组、二分查找排序树、数组模拟链表等)教学中采用了模型化思維教学模式。调查研究及教学实践证明,模型化思维手段可以协助教师将教学重点从知识讲授转移到思维培养上,帮助学生有效地降低学习难度,理解新知,构建新的思维模型并迁移运用,获得有意义的学习,促进学生复杂问题解决能力和计算思维的养成。针对信息技术选考模块“数据与数据结构”的其他内容,如栈、队列等,创设出既符合学生认知又有利于培养学生计算思维的情境模型,并实施模型化思维教学,值得继续研究。
本文为2019年杭州市基教教研课题“指向计算思维培养的高中信息技术教学设计实践研究”(项目编号L2019237)研究成果。

