经济营养配餐的线性规划模型

“民以食为天”，一日三餐直接关系到每个人的身体健康，特别是处于生长发育的学生们，体格、心理和智力等各方面正走向成熟，是长知识和长身体的重要时期。均衡合理的膳食以及良好的饮食行为是学生身体发育以及完成繁重的学业的重要保证，而不合理的膳食行为则会影响身体健康，甚至出现营养性疾病。本文主要考虑在校大学生的经济营养配餐，由于大学生属于无收入消费者，就餐一般均在食堂，所以大学生就餐时经常会考虑到饮食成本，所以研究如何在满足营养与热量的前提下使购买食品的费用最小，实现经济营养配餐，是关系到大学生切身利益的事。
模型的假设及建立
根据营养平衡理论以及大学生实际情况，合理的膳食营养需满足如下要求：
（1）总能量达标。假设大学生每天需要的总能量平均值为P （ P=2700千焦）。早、中、晚热量之比为3：4：3。设早、中、晚餐热量分别为p1、p2、p3，即满足p1：p2：p3=3：4：3。
（2）平衡膳食宝塔要求。其中谷类食物位居底层，每人每天应该吃300 ～ 500 g；蔬菜和水果位于第二层，每天应吃400 ～ 500 g 和l00 ～ 200 g；鱼、禽、肉、蛋等動物性食物位于第三层，每天应该吃l25 ～ 200 g（鱼虾类50 g，畜禽肉50 ～ l00 g，蛋类25 ～ 50 g）；奶类和豆类食物合占第四层，每天应吃奶类及奶制品l00 g 和豆类及豆制品50 g。第五层塔尖是油脂类，每天不超过25 g。由于油脂类含量掌握在烹饪过程中，故本模型不予考虑。
设谷类集合为A{A1，A2，A3，…}，其中A1，A2，…分别表示各种谷物，例如A1表示大米，A2表示面粉；蔬菜类集合为B{B1，B2， B3，…}；水果类集合为C{C1，C2，C3，…}；家禽肉类集合为：D{D1，D2，D2，…}；鱼虾类集合为：E{E1，E2，E3，…}；蛋类集合为：F{F1，F2，F3，…}；奶类的集合为：G{G1，G2，G3，…}；豆类的集合为：H{H1，H2，H3，…}。
根据上述要求，可建立线性规划模型，目标函数是总费用最小，约束条件主要有两个，一个是一个是总能量以及早中晚热量之比，还有一个平衡膳食宝塔要求。
Lingo编程
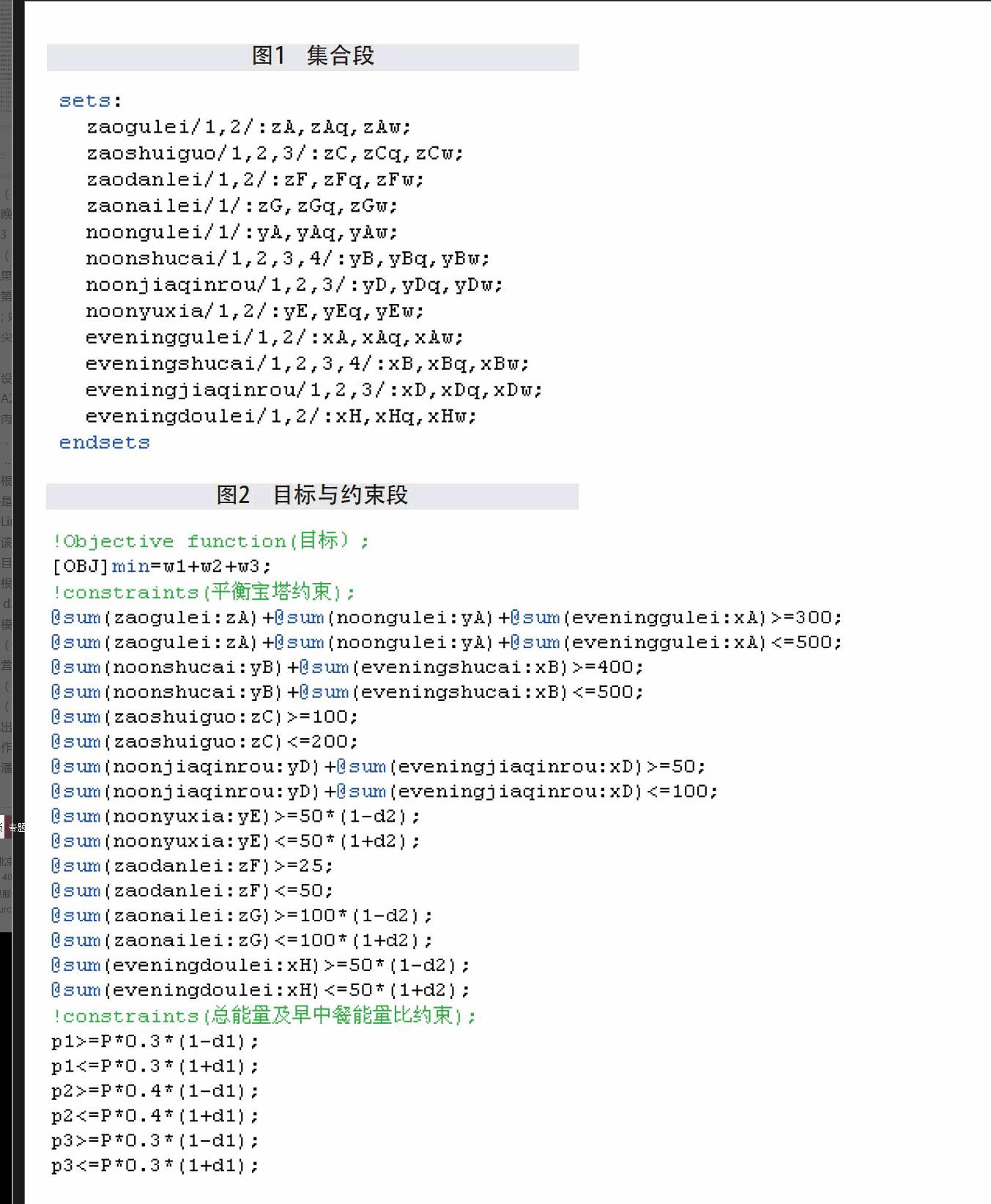
该模型可利用lingo软件编程求解，具体程序如图1和图2所示，图1主要是集合段，图2主要是目标与约束段。图1的集合段预先确定了三餐食物的各种类别及可选数量，此类别及数量可以根据实际情况做不同的改变。图2中的w1、w2、w3分别为早、中、晚餐食物总价格，d1、d2为相对误差量。
模型的求解及结论
（1）该程序结合实际的数据段，即可得出最优解，从而设计出令人满意的食谱方案，既满足营养与能量需求，又使总费用最小。
（2）为了得出不同菜式的食谱方案，只需改变相应的数据段即可。
（3）如考虑性别、年龄、身高、体重及活动量的差别，可改变相应的总热量值P，从而计算出符合自身实际需求的经济食谱方案。
作者简介：
潘敏（1984-），女，汉，江苏泰州，泰州职业技术学院，讲师，硕士。