数学,学什么
田献增
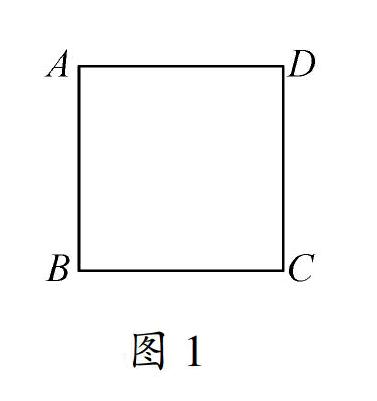
题目 如图1,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
1 忘却的记忆
笔者当看到南京试题的25题时,想起了2005年参加日照市中考试题命题时出的一道题:
一位园艺设计师计划在一块形状为直角三角形且有一个内角为60°的绿化带上种植四种不同的花卉,要求种植的四种花卉分别组成面积相等,形状完全相同的图形图案.某同学为此提供了如图2所示的五种设计方案.其中可以满足园艺设计师要求的有( ).
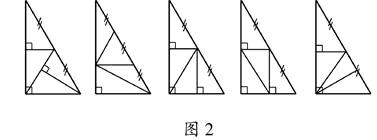
A.2种 B.3种 C.4种 D.5种
本题设计意图是借助学生熟悉30°直角三角板,在考察30°角直角三角形、等边三角形、矩形以及三角形中位线等知识点的同时,还考察了学生综合探究能力或分类思想.题外之意是引导教师在教学或学生在学习时,要注意用数学的眼光观察生活,培养学生的数学意识、数学思考.(解法略)
在命题过程中,原本想命制一道具有探究性的开放题,并以填空题或解答(画图)题形式展示.例如填空题形式:
一位园艺设计师计划在一块形状为直角三角形且有一个内角为60°的绿化带上种植四种不同的花卉,要求种植的四种花卉分别组成面积相等,形状完全相同的几何图案,其中可行的设计方案有 种.
本题从数学的角度考虑,若已经找到n种方案,但没找到第(n+1)种方案,又不能证明多于n(如n+1)种方案不存在.因此就改为试卷中的选择题.
本题与南京中考试题第25题比较,笔者认为无论从数学素材的选择,还是命题角度、意图以及题目分析方法,都有相似之处.
2 题目解答过程中分类方法的探讨
因为本题要求所画出的三角形满足以下条件:A为一个顶点;另外两个顶点(不妨设为E,F)在正方形ABCD的边上;一边长为3;所有大小不同的等腰三角形.因此应先以等腰三角形的“顶点”(注:与三角形顶点含义不同)为标准进行分类讨论.
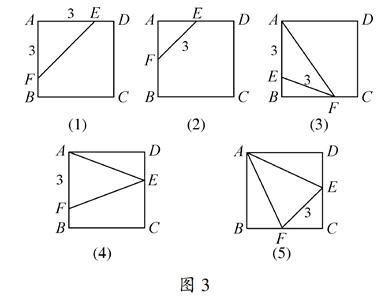
(1)当AE=AF时,此时
①若AE=AF=3,有如图3(1)一个等腰三角形.
②若EF=3,有如图3(2)(5)两个等腰三角形.
(2)当EA=EF时,此时
①若EA=EF=3,当点E在AB上时,有如图3(3)一个等腰三角形;当点E在AD上时,有大小相等、形状相同的三角形,同图3(3).
②若AF=3,当点F在AB上时,有如图3(4)一个等腰三角形;当点F在AD上时,有大小相等、形状相同的三角形,同图3(4).
(3)当FA=FE时,讨论方法同(2).因此本题满足条件的所有等腰三角形如图3所示.
3 对南京第25题设计意图以及价值分析
(1)从本题考察的数学知识角度上看,解答本题用到的知识比较浅显,如正方形、等腰三角形和线段中垂线”等性质以及全等三角形直观判定.
(2)从本题命题目的角度上看,因为该题背景对于学生来说特别熟悉.因此有“出其不意,攻其不备”之效.从学生最熟悉的“生活情境”中提出问题,并且用最基本的数学知识解决问题,这应是中小学数学教育的方向,也是课程标准的要求.“繁、难、偏”或数学内部知识的叠加组合,无益于学生数学学习.培养学生的分析问题,解决问题的数学能力,探究问题的数学能力,深入挖掘日常生活中数学素材,同样可以达到目的.
(3)从本题对教师学生心理影响上看,这样的题目即使学生得分率很低,我想命题者也不会被学生、学生家长以及老师怨为“数学帝”.留给教师和学生的是自身的“反思”和“责备”.倘若是这样,不正是“中考指挥棒”想达到的目的吗?
(4)从本题解题的思想方法上看,除了考察运用“尺规作图”思考问题的意识外,主要考察分类思想和方法.分类思想是数学中非常重要的思想方法.我曾经和“当代教育家”杂志社主任王湘蓉“开过玩笑”——数学学习关键在于“分类”,对于低年级学生来说,要加强分类意识的培养和分类标准教学.学生分类意识薄弱,分类标准不清,难以学好数学.从这个意义上讲,分类或许是数学思维的“核心”,数学能力的“基础”.
事实上,学生对于数学知识掌握的多与寡,走向社会后(培养数学精英除外)对于自身发展影响不大.日本数学家米山国藏说过:“作为知识的数学出校门不到两年就忘了,唯有深深铭记在头脑中的数学的精神、数学的思想、研究的方法和着眼点等,这些随时随地地发生作用,使人终身受益.学生将知识忘却了以后剩下的东西,这其中核心的成分是数学思维.”本题的价值正是在于留给学生的“分类”数学思维和数学的意识与数学的思考.也正是这种数学思想是学生走向社会或继续学习必备的素质.

题目 如图1,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)
1 忘却的记忆
笔者当看到南京试题的25题时,想起了2005年参加日照市中考试题命题时出的一道题:
一位园艺设计师计划在一块形状为直角三角形且有一个内角为60°的绿化带上种植四种不同的花卉,要求种植的四种花卉分别组成面积相等,形状完全相同的图形图案.某同学为此提供了如图2所示的五种设计方案.其中可以满足园艺设计师要求的有( ).

A.2种 B.3种 C.4种 D.5种
本题设计意图是借助学生熟悉30°直角三角板,在考察30°角直角三角形、等边三角形、矩形以及三角形中位线等知识点的同时,还考察了学生综合探究能力或分类思想.题外之意是引导教师在教学或学生在学习时,要注意用数学的眼光观察生活,培养学生的数学意识、数学思考.(解法略)
在命题过程中,原本想命制一道具有探究性的开放题,并以填空题或解答(画图)题形式展示.例如填空题形式:
一位园艺设计师计划在一块形状为直角三角形且有一个内角为60°的绿化带上种植四种不同的花卉,要求种植的四种花卉分别组成面积相等,形状完全相同的几何图案,其中可行的设计方案有 种.
本题从数学的角度考虑,若已经找到n种方案,但没找到第(n+1)种方案,又不能证明多于n(如n+1)种方案不存在.因此就改为试卷中的选择题.
本题与南京中考试题第25题比较,笔者认为无论从数学素材的选择,还是命题角度、意图以及题目分析方法,都有相似之处.
2 题目解答过程中分类方法的探讨
因为本题要求所画出的三角形满足以下条件:A为一个顶点;另外两个顶点(不妨设为E,F)在正方形ABCD的边上;一边长为3;所有大小不同的等腰三角形.因此应先以等腰三角形的“顶点”(注:与三角形顶点含义不同)为标准进行分类讨论.

(1)当AE=AF时,此时
①若AE=AF=3,有如图3(1)一个等腰三角形.
②若EF=3,有如图3(2)(5)两个等腰三角形.
(2)当EA=EF时,此时
①若EA=EF=3,当点E在AB上时,有如图3(3)一个等腰三角形;当点E在AD上时,有大小相等、形状相同的三角形,同图3(3).
②若AF=3,当点F在AB上时,有如图3(4)一个等腰三角形;当点F在AD上时,有大小相等、形状相同的三角形,同图3(4).
(3)当FA=FE时,讨论方法同(2).因此本题满足条件的所有等腰三角形如图3所示.
3 对南京第25题设计意图以及价值分析
(1)从本题考察的数学知识角度上看,解答本题用到的知识比较浅显,如正方形、等腰三角形和线段中垂线”等性质以及全等三角形直观判定.
(2)从本题命题目的角度上看,因为该题背景对于学生来说特别熟悉.因此有“出其不意,攻其不备”之效.从学生最熟悉的“生活情境”中提出问题,并且用最基本的数学知识解决问题,这应是中小学数学教育的方向,也是课程标准的要求.“繁、难、偏”或数学内部知识的叠加组合,无益于学生数学学习.培养学生的分析问题,解决问题的数学能力,探究问题的数学能力,深入挖掘日常生活中数学素材,同样可以达到目的.
(3)从本题对教师学生心理影响上看,这样的题目即使学生得分率很低,我想命题者也不会被学生、学生家长以及老师怨为“数学帝”.留给教师和学生的是自身的“反思”和“责备”.倘若是这样,不正是“中考指挥棒”想达到的目的吗?
(4)从本题解题的思想方法上看,除了考察运用“尺规作图”思考问题的意识外,主要考察分类思想和方法.分类思想是数学中非常重要的思想方法.我曾经和“当代教育家”杂志社主任王湘蓉“开过玩笑”——数学学习关键在于“分类”,对于低年级学生来说,要加强分类意识的培养和分类标准教学.学生分类意识薄弱,分类标准不清,难以学好数学.从这个意义上讲,分类或许是数学思维的“核心”,数学能力的“基础”.
事实上,学生对于数学知识掌握的多与寡,走向社会后(培养数学精英除外)对于自身发展影响不大.日本数学家米山国藏说过:“作为知识的数学出校门不到两年就忘了,唯有深深铭记在头脑中的数学的精神、数学的思想、研究的方法和着眼点等,这些随时随地地发生作用,使人终身受益.学生将知识忘却了以后剩下的东西,这其中核心的成分是数学思维.”本题的价值正是在于留给学生的“分类”数学思维和数学的意识与数学的思考.也正是这种数学思想是学生走向社会或继续学习必备的素质.

