2015年浙江省绍兴市中考填空压轴题的赏析与感悟
沈岳夫
题目 (2015年浙江绍兴)实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图1所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升56cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.图1

本题短小、简洁,条件清晰.虽涉及知识点不多,但要获得满分不容易,是一道命制较为成功的代数压轴题.笔者通过QQ群与许多教师交流此题,收获颇丰,现予以展示,以飨读者.
1 情境新,体现试题的原创性与公平性
试题以学生熟悉的连通器为背景,给学生常见的数学知识赋予新意,这样的情境设置表面平凡,内含新意,原创性强.在内容上,考题素材新颖、纯汁原创,以考查给定3个容器内约定的水位差变化为己任,命题视角一扫往昔[1].试题的内容,学生、教师都不曾见过或预见过,从而在内容上保证了试卷评价的公平公正性.在题型上,勇于推陈出新,开启以代数题作为填空题的压轴题之先河,这是一次大胆的挑战与突破,也符合《课程标准(2011年版)》教学理念,要让学生初步学会从数学的角度发现问题和提出问题,综合运用数学知识解决简单的实际问题,增强应用意识,提高实践能力.
2 立意新,凸显试题的基础性与思想性
根据《课程标准(2011年版)》的要求,学生通过初中三年的学习,应该掌握计算、证明、数据处理、数学建模等基本技能.对基本技能的熟练掌握,不仅能直接加深学生对基础知识的理解,还有助于提高学生分析问题及解决问题的能力.试题从考查的知识点上看,主要涉及一元一次方程,真正体现关注本质,关注思维,关注素养;从考查的能力层面上看,重点对学生的空间观念与想象、几何直观与推理、代数计算与化简等综合数学能力进行了全面的考查;从考查的思想方法上看,直接或间接地体现着一些数学思想或方法,如转化思想、数形结合思想、分类讨论思想、方程思想在问题的解决过程中有很明显的体现.
3 构思新,展现试题的多样性与差异性
试题构思新,解法多样,给学生留有较大的思维空间,学生在解题过程中可以以自己擅长的方式构思或寻求解决问题的方法,有利于学生能力的主动发挥,创造力的充分发掘[2].
解法1 根据题意,可设甲、乙、丙的底面积分别为S、4S、S,向乙、丙注水的时间为t分钟.因为每分钟同时向乙和丙注入相同量的水,所以当注水1分钟可求出丙的水位上升高度:4S×56=S×h丙,解得h丙=103,所以注水1分钟,丙的水位上升为103cm.

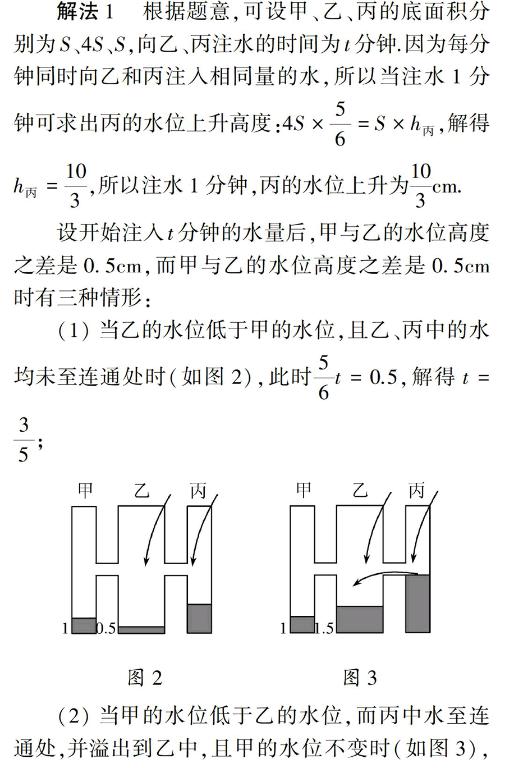
设开始注入t分钟的水量后,甲与乙的水位高度之差是0.5cm,而甲与乙的水位高度之差是0.5cm时有三种情形:

不难看出,这些方法从思维策略上,都是通过已知量、未知量的关系,寻求等量建立方程.解法1侧重于“算二次”,从不同视角找等量关系,解法2侧重于用总进水量除以速度和来解决问题;从思想方法上,都体现了转化及分类讨论的思想.该题解法多样,凸显本质,有效地考查了学生平时积累的方法与能力,只要教与学的过程注重“四基”,学生就会充满信心解答本题.而且本题具有较大的数学思维空间、解法自由度,扩充了思维内涵,在体现能力立意的同时,适合具有不同思维特点的学生探究思路,展现“不同人在数学上得到不同的发展”的课标理念.这对于开阔学生思维视野、培养和训练学生思维能力及教师今后的教学导向都具有极大的教育价值.
参考文献
[1] 戴向阳,戴向前.创新多解拓展[J].中学数学(下),2014(10):79-81.
[2] 张仁华.“菱”动一转“新”光闪耀[J].中学数学教学参考(中旬),2014(9):56-57.
题目 (2015年浙江绍兴)实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两个相同的管子在容器的5cm高度处连通(即管子底端离容器底5cm),现三个容器中,只有甲中有水,水位高1cm,如图1所示.若每分钟同时向乙和丙注入相同量的水,开始注水1分钟,乙的水位上升56cm,则开始注入 分钟的水量后,甲与乙的水位高度之差是0.5cm.图1

本题短小、简洁,条件清晰.虽涉及知识点不多,但要获得满分不容易,是一道命制较为成功的代数压轴题.笔者通过QQ群与许多教师交流此题,收获颇丰,现予以展示,以飨读者.
1 情境新,体现试题的原创性与公平性
试题以学生熟悉的连通器为背景,给学生常见的数学知识赋予新意,这样的情境设置表面平凡,内含新意,原创性强.在内容上,考题素材新颖、纯汁原创,以考查给定3个容器内约定的水位差变化为己任,命题视角一扫往昔[1].试题的内容,学生、教师都不曾见过或预见过,从而在内容上保证了试卷评价的公平公正性.在题型上,勇于推陈出新,开启以代数题作为填空题的压轴题之先河,这是一次大胆的挑战与突破,也符合《课程标准(2011年版)》教学理念,要让学生初步学会从数学的角度发现问题和提出问题,综合运用数学知识解决简单的实际问题,增强应用意识,提高实践能力.
2 立意新,凸显试题的基础性与思想性
根据《课程标准(2011年版)》的要求,学生通过初中三年的学习,应该掌握计算、证明、数据处理、数学建模等基本技能.对基本技能的熟练掌握,不仅能直接加深学生对基础知识的理解,还有助于提高学生分析问题及解决问题的能力.试题从考查的知识点上看,主要涉及一元一次方程,真正体现关注本质,关注思维,关注素养;从考查的能力层面上看,重点对学生的空间观念与想象、几何直观与推理、代数计算与化简等综合数学能力进行了全面的考查;从考查的思想方法上看,直接或间接地体现着一些数学思想或方法,如转化思想、数形结合思想、分类讨论思想、方程思想在问题的解决过程中有很明显的体现.
3 构思新,展现试题的多样性与差异性
试题构思新,解法多样,给学生留有较大的思维空间,学生在解题过程中可以以自己擅长的方式构思或寻求解决问题的方法,有利于学生能力的主动发挥,创造力的充分发掘[2].

解法1 根据题意,可设甲、乙、丙的底面积分别为S、4S、S,向乙、丙注水的时间为t分钟.因为每分钟同时向乙和丙注入相同量的水,所以当注水1分钟可求出丙的水位上升高度:4S×56=S×h丙,解得h丙=103,所以注水1分钟,丙的水位上升为103cm.

设开始注入t分钟的水量后,甲与乙的水位高度之差是0.5cm,而甲与乙的水位高度之差是0.5cm时有三种情形:

不难看出,这些方法从思维策略上,都是通过已知量、未知量的关系,寻求等量建立方程.解法1侧重于“算二次”,从不同视角找等量关系,解法2侧重于用总进水量除以速度和来解决问题;从思想方法上,都体现了转化及分类讨论的思想.该题解法多样,凸显本质,有效地考查了学生平时积累的方法与能力,只要教与学的过程注重“四基”,学生就会充满信心解答本题.而且本题具有较大的数学思维空间、解法自由度,扩充了思维内涵,在体现能力立意的同时,适合具有不同思维特点的学生探究思路,展现“不同人在数学上得到不同的发展”的课标理念.这对于开阔学生思维视野、培养和训练学生思维能力及教师今后的教学导向都具有极大的教育价值.
参考文献
[1] 戴向阳,戴向前.创新多解拓展[J].中学数学(下),2014(10):79-81.
[2] 张仁华.“菱”动一转“新”光闪耀[J].中学数学教学参考(中旬),2014(9):56-57.

