另眼看折叠，别有“圆汁圆味”

张振中






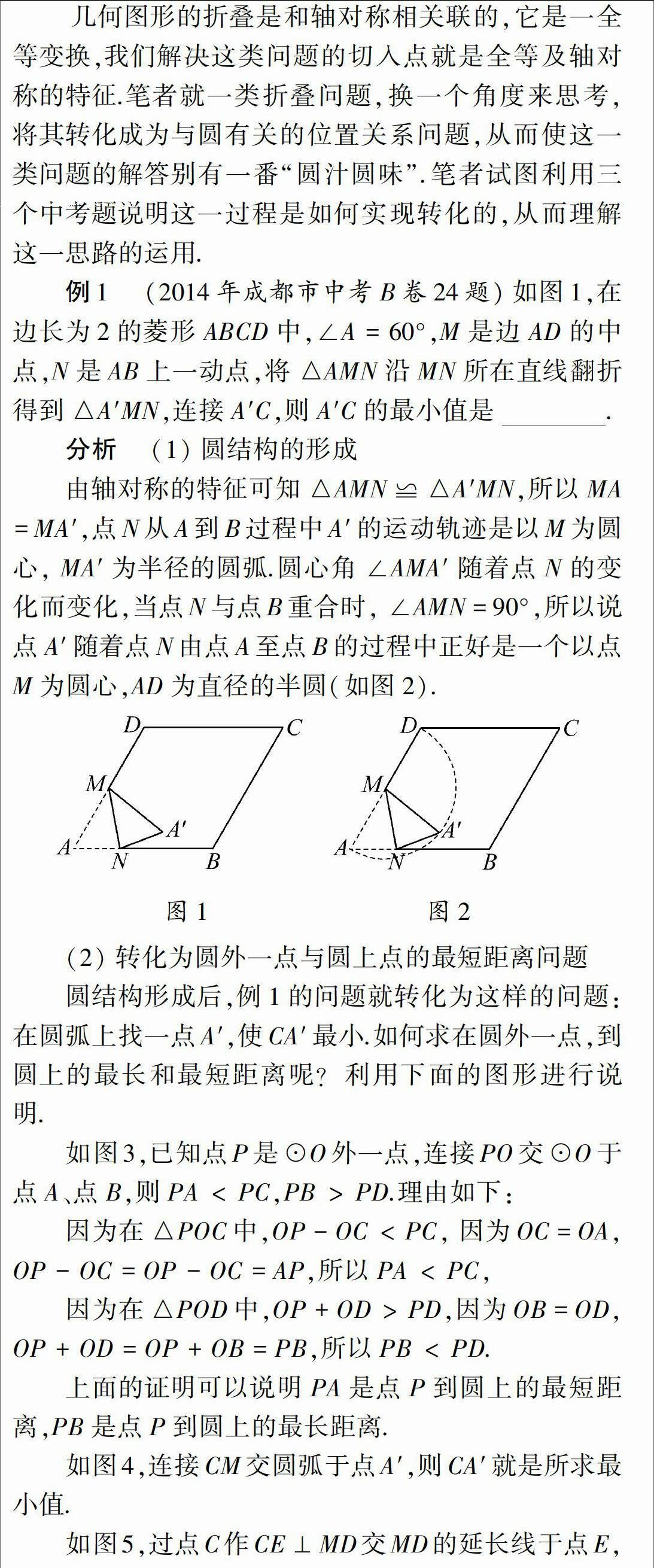
几何图形的折叠是和轴对称相关联的，它是一全等变换，我们解决这类问题的切入点就是全等及轴对称的特征.笔者就一类折叠问题，换一个角度来思考，将其转化成为与圆有关的位置关系问题，从而使这一类问题的解答别有一番“圆汁圆味”.笔者试图利用三个中考题说明这一过程是如何实现转化的，从而理解这一思路的运用.
相关文章！
  • 连接体问题中两物体物理量的关

    吴春晓高中常见的连接体问题主要的表现形式有：两个物体直接接触、两个物体用轻绳或轻杆连接、两个物体用弹簧连接.整体法并不适用于所有

  • 浅析信息技术在机电教学中的融

    皮晓虹摘要：随着“互联网+”时代的到来，信息技术在职业教育发展中具有极其深远的影响。2014年，《现代职业教育体系建设规划（2014-2020）》对

  • 质谱法测定水中溶解氙的含量及

    李军杰+刘汉彬 张佳+韩娟+金贵善+张建锋<br />
    <br />
    <br />
    <br />
    摘要 利用设计的一套水样中提取并分离Xe的装置，与稀有气体质谱