初中物理电路问题解题思路点拨
周雨婷 周新雅
电学一直是初中生的一个学习难点,很多学生到了初二,由于电学知识的加入,成绩直线下滑.对于普通的电路问题,要摸清其规律其实并不难.关键是要帮助学生理清解题思路,避免出现拿到题目又无从下手的情况.
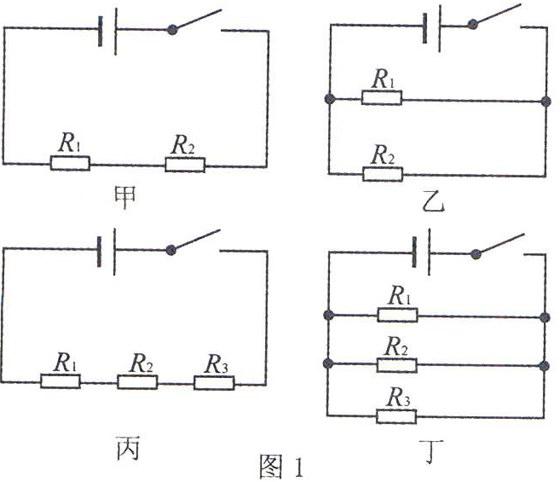
首先是判断电路的类型(判断电路是串联还是并联),这是审题的关键,如果这个问题弄错了,之后的解题将南辕北辙.题面通常不会那么明显地给出典型的串并联电路.我们要做的就是把较复杂的电路图简化为图1中的最简形式,共有以下四种方法:
其一是“定义法”.
1.串联电路:把电路元件逐个顺次连接起来的电路(首尾相连)
2.并联电路:把电路元件并列连接起来的电路(首首相连,尾尾相连)
问题的关键是如何判断首和尾,这里可以教给学生把与正极相连的那一端叫做首并标上“+”,把与负极相连的那一端叫做尾,并标上“-”,只要是正极和负极相连就是串联电路,正极和正极、负极和负极相连的电路就是并联电路.
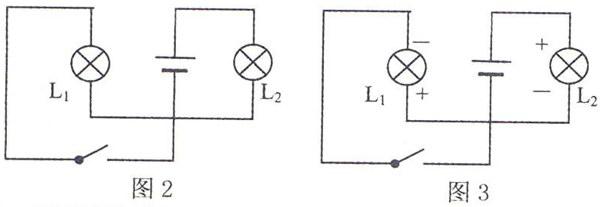
例1利用定义法判断图2中电路的类型.
分析利用定义法按图3标注好正负,可以看出有一端正负直接相连,所以此电路为串联电路.
其二是“拆除法”.
这个方法较容易掌握,使用起来也比较简单,利用的是串并联电路的特点.
1.串联电路:各用电器相互影响,电路某一处断开(用手遮住),整个电路不工作.
2.并联电路:各支路独立工作,互相不影响.
其三是“模拟电流法”.
此方法尤其适用于出现短路、断路(开路)的电路.把自己当成电流,那么电流的走向是从正极出发回到负极.那么过程中遇到节点的话就相当于到了分叉路口,电流就要选择没有阻碍(电阻)的路走,就出现短路的情形;如果遇到走不通的路,就是断路情形;当每条路都有阻碍(电阻),就会按阻碍大小分流走.
其四是“滑移法”.
在识别电路时,不论导线有多长,只要其间没有用电器或电源,则导线的两端点都可看成同一点,用此方法可以缩短导线移动变换电路,从而达到最终的简化电路.
其次是判断电流表电压表的测定对象,并把它们还原到简化电路中.
1.如何判断电压表的测定对象
方法一:滑移法
利用滑移法找出与电压表直接并联的那部分电路元件,则电压表测量该部分电压.
方法二:去源法
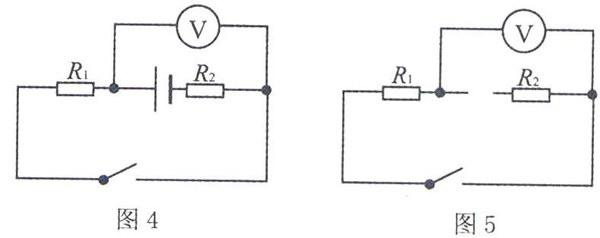
去掉电源(用手遮住电源),电压表和哪个用电器构成回路则是测谁的电压.例如图4所示,我们将电源去掉,原电路将变成图5的形式,很容易看出:电压表只与电阻R1组成闭合回路,它测的是R1两端的电压.
2.如何判断电流表的测定对象
方法一:断开电流表用电器因断路不能工作.
将电流表断开,哪些用电器(因断路)不能正常工作,则断开的电流表测这些用电器的电流.
例2试判断图6中的电流表A1、A2、A3分别测哪些灯泡的电流.
分析当断开A3时,L3断路,故A3是测L3的电流. ? 当断开A2时,L2断路,故A2是测L2的电流.
当断开A1时,L1、L2、L3均断路,则A1是测L1、L2、L3并联的总电流.
方法二:断开电流表用电器因短路不能工作.
将电流表断开,哪些用电器(因短路)不能正常工作,则该电表测的是通过哪些用电器的电流.
例3试判断图7中的电流表A1、A2、A3分别测哪些灯泡的电流.
分析当断开A1时,L1、L2、L3均断路,则A1是测L1、L2、L3并联的总电流.
当断开A2时,把A1看做导线,L1、L2均因为短路而不工作,所以A2是测L1、L2的电流.
当断开A1时,把A2看做导线,L2、L3均因短路而不工作,所以A1是测L2、L3的电流.
注意:断开后发现所用用电器都能正常工作,则该电路中出现短路情况则不能用以上方法.
例如观察图8发现,断开A2所有用电器均能正常工作.仔细观察可以看出,这个电路本身就是一个发生了短路的电路.闭合开关L2、L3都因短路不能工作,两个电流表示数相同,都只测了L1的电流.
所以在使用以上两方法时,先看看电路中是否已经出现短路情形,是否是一个正常工作的电路.
最后是运用串联电路或并联电路的电流、电压、电阻等规律和欧姆定律解决具体的问题.
这里要用到几个常见的电压、电流、电阻间的规律,以两个电阻的串并联为例.
1.欧姆定律:每个电阻都有一套属于它的欧姆定律
I1=U1R1、I2=U2R2、I总=U总R总.
2.串联电路中电流、电压、电阻间的关系
(1)电流关系:I总=I1=I2;
(2)电压关系:U总=U1+U2;
(3)电阻关系:R总=R1+R2.
3.并联电路中的电流、电压、电阻间的关系
(1)电流关系:I总=I1+I2;
(2)电压关系:U总=U1=U2;
(3)电阻关系:1R总=1R1+1R2.
这里可以用“家庭与家庭间的关系”这个形象的比喻描述以上关系.电压在等式中地位较大是“爸爸”,电流是“妈妈”,电阻是“孩子”,把以上关系中的“U”换成“爸爸”,“I”换成“妈妈”,“R”换成“孩子”.第1项中的欧姆定律可以理解为家庭内部间的关系,但是每个家庭的个体都不是孤立的,它们之间也有一定的社会关系,也就是第2、第3项中的串并联电压、电流、电阻间的关系.
我们甚至还知道串联的分压和并联的分流也不是乱分的,它是和孩子的大小有关.这样做不仅帮助同学记忆而且提高了知识的趣味性.
本文以一道武汉市2014中考题为例说明笔者的解题思路的优势.在没有教此方法前,笔者给学生讲解了这道题,过了一段时间再给他们做,由于题目有一定的难度,大部分同学依旧无法下手.接着笔者用这样的一套流程进行讲解,学生马上觉得思路清晰多了.
[2014年武汉市]如图9所示的电路中,电源电压保持不变,R1=10 Ω.当开关S1闭合,S2、S3断开时,电压表的示数为U1,R2消耗的功率为P2;当开关S1、S2、S3都闭合时,电压表的示数为U′1,R2消耗的功率为P′2,且电流表A1的示数为0.9 A.已知U1∶U′1=1∶6,P2∶P′2=1∶9,下列结论错误的是
A.开关S1闭合,S2、S3断开时,电流表A2的示数为0.1 A
B.开关S1闭合,S2、S3断开时,电路消耗的总功率为0.6 W
C.开关S1、S2、S3都闭合时,电流表A2的示数为1.1 A
D.开关S1、S2、S3都闭合时,R2和R3消耗的总功率5.4 W
分析审题后发现这是一道开关引起的动态电路问题,我们应该分开讨论“开关S1闭合,S2、S3 断开”和“开关S1、S2、S3都闭合”等两种情形.
对于情形一:开关S1闭合,S2、S3 断开,按照电流表相当于导线,电压表相当于断路的原则,先去掉电压表电流表.
第一步分析出该电路为串联电路,并作出简化电路图.
第二步判断出A2和V的测定对象,并把它们补充入简化电路中.第一步和第二步结束后可作出图10.
对于情形二:当开关S1、S2、S3都闭合,按照上面的步骤同样可以作出简化电路图(图11).
第三步:需要梳理两幅图中各个物理量的关系.假设图10中的干路电流大小为I.
已知R1电阻可列关系式:
U1=IR1=10I,
由已知U1∶U′1=1∶6,
可得U′1=60I=E,R总=60 Ω.
而R2=I2R,P′2=I22R,
根据比例关系P1∶P′2=1∶9得出I2=3I,
I1=U′1R1=60I10=6I.
由I1+I2=6I+3I=9I=0.9 A,得I=0.1 A,所以A项正确.
P=I2R总=0.01×60 W=0.6 W,B项正确.
现在可以把能算出了的量整理一下:
I1=0.6,I2=0.3,E=6 V,R2=EI2=20 Ω,
R3=(60-10-20) Ω=30 Ω,I3=ER3=0.2 A,
A2的示数为I1+I2+I3=(0.9+0.2) A=1.1 A,C项正确.
P=I22R2+I23R3=1.8+1.2=3 W,
所以D项错误.
分析这是一道动态电路问题,但解题精髓仍然是笔者前面提到的三步,只是我们要作出两种情形的简化电路图.
总之,电学的题目其实并不那么复杂.我们要做的首先是掌握好基本的物理概念和规律并做到熟练应用,再结合刚刚的思维方法,大部分电学问题都能迎刃而解了.



电学一直是初中生的一个学习难点,很多学生到了初二,由于电学知识的加入,成绩直线下滑.对于普通的电路问题,要摸清其规律其实并不难.关键是要帮助学生理清解题思路,避免出现拿到题目又无从下手的情况.
首先是判断电路的类型(判断电路是串联还是并联),这是审题的关键,如果这个问题弄错了,之后的解题将南辕北辙.题面通常不会那么明显地给出典型的串并联电路.我们要做的就是把较复杂的电路图简化为图1中的最简形式,共有以下四种方法:
其一是“定义法”.
1.串联电路:把电路元件逐个顺次连接起来的电路(首尾相连)
2.并联电路:把电路元件并列连接起来的电路(首首相连,尾尾相连)
问题的关键是如何判断首和尾,这里可以教给学生把与正极相连的那一端叫做首并标上“+”,把与负极相连的那一端叫做尾,并标上“-”,只要是正极和负极相连就是串联电路,正极和正极、负极和负极相连的电路就是并联电路.
例1利用定义法判断图2中电路的类型.
分析利用定义法按图3标注好正负,可以看出有一端正负直接相连,所以此电路为串联电路.
其二是“拆除法”.
这个方法较容易掌握,使用起来也比较简单,利用的是串并联电路的特点.
1.串联电路:各用电器相互影响,电路某一处断开(用手遮住),整个电路不工作.
2.并联电路:各支路独立工作,互相不影响.
其三是“模拟电流法”.
此方法尤其适用于出现短路、断路(开路)的电路.把自己当成电流,那么电流的走向是从正极出发回到负极.那么过程中遇到节点的话就相当于到了分叉路口,电流就要选择没有阻碍(电阻)的路走,就出现短路的情形;如果遇到走不通的路,就是断路情形;当每条路都有阻碍(电阻),就会按阻碍大小分流走.
其四是“滑移法”.
在识别电路时,不论导线有多长,只要其间没有用电器或电源,则导线的两端点都可看成同一点,用此方法可以缩短导线移动变换电路,从而达到最终的简化电路.
其次是判断电流表电压表的测定对象,并把它们还原到简化电路中.
1.如何判断电压表的测定对象
方法一:滑移法
利用滑移法找出与电压表直接并联的那部分电路元件,则电压表测量该部分电压.
方法二:去源法
去掉电源(用手遮住电源),电压表和哪个用电器构成回路则是测谁的电压.例如图4所示,我们将电源去掉,原电路将变成图5的形式,很容易看出:电压表只与电阻R1组成闭合回路,它测的是R1两端的电压.
2.如何判断电流表的测定对象
方法一:断开电流表用电器因断路不能工作.
将电流表断开,哪些用电器(因断路)不能正常工作,则断开的电流表测这些用电器的电流.
例2试判断图6中的电流表A1、A2、A3分别测哪些灯泡的电流.
分析当断开A3时,L3断路,故A3是测L3的电流. ? 当断开A2时,L2断路,故A2是测L2的电流.
当断开A1时,L1、L2、L3均断路,则A1是测L1、L2、L3并联的总电流.
方法二:断开电流表用电器因短路不能工作.
将电流表断开,哪些用电器(因短路)不能正常工作,则该电表测的是通过哪些用电器的电流.
例3试判断图7中的电流表A1、A2、A3分别测哪些灯泡的电流.
分析当断开A1时,L1、L2、L3均断路,则A1是测L1、L2、L3并联的总电流.
当断开A2时,把A1看做导线,L1、L2均因为短路而不工作,所以A2是测L1、L2的电流.
当断开A1时,把A2看做导线,L2、L3均因短路而不工作,所以A1是测L2、L3的电流.
注意:断开后发现所用用电器都能正常工作,则该电路中出现短路情况则不能用以上方法.
例如观察图8发现,断开A2所有用电器均能正常工作.仔细观察可以看出,这个电路本身就是一个发生了短路的电路.闭合开关L2、L3都因短路不能工作,两个电流表示数相同,都只测了L1的电流.
所以在使用以上两方法时,先看看电路中是否已经出现短路情形,是否是一个正常工作的电路.
最后是运用串联电路或并联电路的电流、电压、电阻等规律和欧姆定律解决具体的问题.
这里要用到几个常见的电压、电流、电阻间的规律,以两个电阻的串并联为例.
1.欧姆定律:每个电阻都有一套属于它的欧姆定律
I1=U1R1、I2=U2R2、I总=U总R总.
2.串联电路中电流、电压、电阻间的关系
(1)电流关系:I总=I1=I2;
(2)电压关系:U总=U1+U2;
(3)电阻关系:R总=R1+R2.
3.并联电路中的电流、电压、电阻间的关系
(1)电流关系:I总=I1+I2;
(2)电压关系:U总=U1=U2;
(3)电阻关系:1R总=1R1+1R2.
这里可以用“家庭与家庭间的关系”这个形象的比喻描述以上关系.电压在等式中地位较大是“爸爸”,电流是“妈妈”,电阻是“孩子”,把以上关系中的“U”换成“爸爸”,“I”换成“妈妈”,“R”换成“孩子”.第1项中的欧姆定律可以理解为家庭内部间的关系,但是每个家庭的个体都不是孤立的,它们之间也有一定的社会关系,也就是第2、第3项中的串并联电压、电流、电阻间的关系.
我们甚至还知道串联的分压和并联的分流也不是乱分的,它是和孩子的大小有关.这样做不仅帮助同学记忆而且提高了知识的趣味性.
本文以一道武汉市2014中考题为例说明笔者的解题思路的优势.在没有教此方法前,笔者给学生讲解了这道题,过了一段时间再给他们做,由于题目有一定的难度,大部分同学依旧无法下手.接着笔者用这样的一套流程进行讲解,学生马上觉得思路清晰多了.
[2014年武汉市]如图9所示的电路中,电源电压保持不变,R1=10 Ω.当开关S1闭合,S2、S3断开时,电压表的示数为U1,R2消耗的功率为P2;当开关S1、S2、S3都闭合时,电压表的示数为U′1,R2消耗的功率为P′2,且电流表A1的示数为0.9 A.已知U1∶U′1=1∶6,P2∶P′2=1∶9,下列结论错误的是
A.开关S1闭合,S2、S3断开时,电流表A2的示数为0.1 A
B.开关S1闭合,S2、S3断开时,电路消耗的总功率为0.6 W
C.开关S1、S2、S3都闭合时,电流表A2的示数为1.1 A
D.开关S1、S2、S3都闭合时,R2和R3消耗的总功率5.4 W
分析审题后发现这是一道开关引起的动态电路问题,我们应该分开讨论“开关S1闭合,S2、S3 断开”和“开关S1、S2、S3都闭合”等两种情形.
对于情形一:开关S1闭合,S2、S3 断开,按照电流表相当于导线,电压表相当于断路的原则,先去掉电压表电流表.
第一步分析出该电路为串联电路,并作出简化电路图.
第二步判断出A2和V的测定对象,并把它们补充入简化电路中.第一步和第二步结束后可作出图10.
对于情形二:当开关S1、S2、S3都闭合,按照上面的步骤同样可以作出简化电路图(图11).
第三步:需要梳理两幅图中各个物理量的关系.假设图10中的干路电流大小为I.
已知R1电阻可列关系式:
U1=IR1=10I,
由已知U1∶U′1=1∶6,
可得U′1=60I=E,R总=60 Ω.
而R2=I2R,P′2=I22R,
根据比例关系P1∶P′2=1∶9得出I2=3I,
I1=U′1R1=60I10=6I.
由I1+I2=6I+3I=9I=0.9 A,得I=0.1 A,所以A项正确.
P=I2R总=0.01×60 W=0.6 W,B项正确.
现在可以把能算出了的量整理一下:
I1=0.6,I2=0.3,E=6 V,R2=EI2=20 Ω,
R3=(60-10-20) Ω=30 Ω,I3=ER3=0.2 A,
A2的示数为I1+I2+I3=(0.9+0.2) A=1.1 A,C项正确.
P=I22R2+I23R3=1.8+1.2=3 W,
所以D项错误.
分析这是一道动态电路问题,但解题精髓仍然是笔者前面提到的三步,只是我们要作出两种情形的简化电路图.
总之,电学的题目其实并不那么复杂.我们要做的首先是掌握好基本的物理概念和规律并做到熟练应用,再结合刚刚的思维方法,大部分电学问题都能迎刃而解了.

