用线段简图巧解比热容问题
王平洲

初中物理教学中,常常会遇到一类有关比热容的问题,用公式Q=cmΔt去推导,过程很繁烦,很难得到结果.教学中,用线段简图与公式分析结合的方法就很容易解决这类问题:用一些水平线的高低位置表示温度高低,用竖直线段表示温度的变化量,再结合公式Q=cmΔt作简单推理,便可得到结果.对解决这类问题能起到简单易懂、化繁为简的作用.
例1质量和温度都相同的甲、乙两物体,将甲投入一杯热水中,达到热平衡时,水温下降Δt,将甲取出,再把乙投入这杯热水中,达到热平衡时,水温又下降Δt(若热量和水量的损失可忽略不计),则甲、乙两物体比热容
A.c甲>c乙B.c甲
说明此题若仅用公式Q=cmΔt以数学方法推导,甲、乙两物体的温度变化量Δt是不容易确定的,过程很繁烦,很难得到结果.但用线段简图,很容易将温度变化量Δt显示出来,就省去了用数学方法分析得出温度变化量Δt的繁烦过程,起到化繁为简的作用.
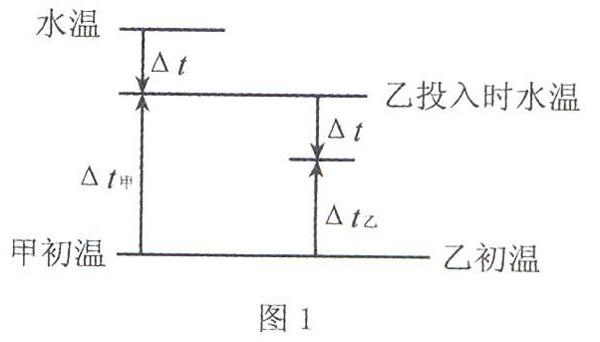
图析甲、乙两物体温度相同,将甲、乙投入水中,达到热平衡时,水温下降Δt,说明水初温高,甲初温低.如图1所示,水温在高位置,甲初温在低位置.将甲投入水中,达到热平衡时,水温下降Δt,那么甲温度就升高Δt甲,把Δt、Δt甲都用竖直线段的长度表示出来.同理,再把乙投入这杯水中,达到热平衡时,水温又下降Δt,那么乙温度就升高Δt乙,把Δt、Δt乙也都用竖直线段的长度表示出来.这就画出了温度变化简图.
推理此题中,甲、乙两物体分别投入水中后,水温都下降Δt,由Q放=cmΔt知,水放出的热量相同,则甲和乙吸收水的热量相同,即Q甲吸=Q乙吸,而甲、乙两物体质量相同,m甲=m乙,由Q吸=cmΔt可知,要比较c甲、c乙的大小,需知Δt甲、Δt乙的大小,由线段简图,一目了然,很容易看出Δt甲>Δt乙,所以c甲
A.c甲>c乙>c丙B.c甲
分析此题若用纯公式理论分析推导,涉及的物理量很多,步骤更复杂,很难得出结论.但用线段简图处理更直观、更简捷(图2).
由图2,ΔtA<ΔtB<ΔtC,即A、B、C放出的热量QA放Δt乙>Δt丙,且m甲=m乙=m丙,由Q吸=cmΔt知,Q甲吸最小,Q乙吸次之,Q丙吸最大,故c甲最小,c乙次之,c丙最大,所以c甲
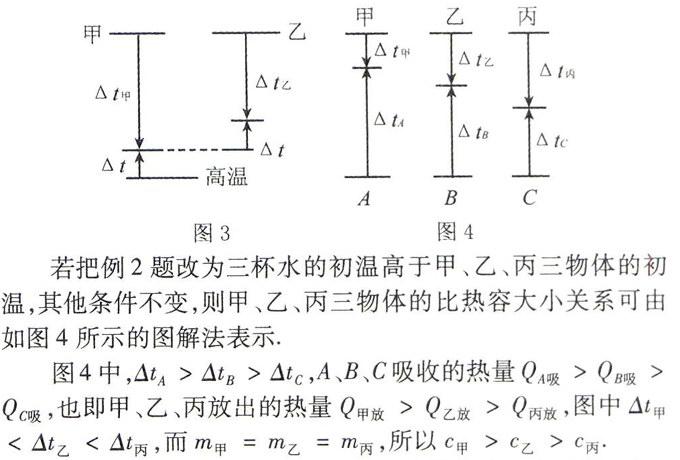
图3中,水温都上升Δt,由Q吸=cmΔt知,水吸收的热量相同,即甲、乙放出的热量相同,由Q放=cmΔt,图中Δt甲>Δt乙,则c甲
图4中,ΔtA>ΔtB>ΔtC ,A、B、C吸收的热量QA吸>QB吸>QC吸,也即甲、乙、丙放出的热量Q甲放>Q乙放>Q丙放,图中Δt甲<Δt乙<Δt丙,而m甲=m乙=m丙,所以c甲>c乙>c丙.
上述方法是把题目中的温度条件转换成位置高度线,从而将难以分析的温度变化量Δt直观地显示出来,便于用公式Q=cmΔt分析比较,得出结论,避免了大量的数学推导过程.



初中物理教学中,常常会遇到一类有关比热容的问题,用公式Q=cmΔt去推导,过程很繁烦,很难得到结果.教学中,用线段简图与公式分析结合的方法就很容易解决这类问题:用一些水平线的高低位置表示温度高低,用竖直线段表示温度的变化量,再结合公式Q=cmΔt作简单推理,便可得到结果.对解决这类问题能起到简单易懂、化繁为简的作用.
例1质量和温度都相同的甲、乙两物体,将甲投入一杯热水中,达到热平衡时,水温下降Δt,将甲取出,再把乙投入这杯热水中,达到热平衡时,水温又下降Δt(若热量和水量的损失可忽略不计),则甲、乙两物体比热容
A.c甲>c乙B.c甲
说明此题若仅用公式Q=cmΔt以数学方法推导,甲、乙两物体的温度变化量Δt是不容易确定的,过程很繁烦,很难得到结果.但用线段简图,很容易将温度变化量Δt显示出来,就省去了用数学方法分析得出温度变化量Δt的繁烦过程,起到化繁为简的作用.
图析甲、乙两物体温度相同,将甲、乙投入水中,达到热平衡时,水温下降Δt,说明水初温高,甲初温低.如图1所示,水温在高位置,甲初温在低位置.将甲投入水中,达到热平衡时,水温下降Δt,那么甲温度就升高Δt甲,把Δt、Δt甲都用竖直线段的长度表示出来.同理,再把乙投入这杯水中,达到热平衡时,水温又下降Δt,那么乙温度就升高Δt乙,把Δt、Δt乙也都用竖直线段的长度表示出来.这就画出了温度变化简图.
推理此题中,甲、乙两物体分别投入水中后,水温都下降Δt,由Q放=cmΔt知,水放出的热量相同,则甲和乙吸收水的热量相同,即Q甲吸=Q乙吸,而甲、乙两物体质量相同,m甲=m乙,由Q吸=cmΔt可知,要比较c甲、c乙的大小,需知Δt甲、Δt乙的大小,由线段简图,一目了然,很容易看出Δt甲>Δt乙,所以c甲
A.c甲>c乙>c丙B.c甲
分析此题若用纯公式理论分析推导,涉及的物理量很多,步骤更复杂,很难得出结论.但用线段简图处理更直观、更简捷(图2).
由图2,ΔtA<ΔtB<ΔtC,即A、B、C放出的热量QA放
图3中,水温都上升Δt,由Q吸=cmΔt知,水吸收的热量相同,即甲、乙放出的热量相同,由Q放=cmΔt,图中Δt甲>Δt乙,则c甲
图4中,ΔtA>ΔtB>ΔtC ,A、B、C吸收的热量QA吸>QB吸>QC吸,也即甲、乙、丙放出的热量Q甲放>Q乙放>Q丙放,图中Δt甲<Δt乙<Δt丙,而m甲=m乙=m丙,所以c甲>c乙>c丙.
上述方法是把题目中的温度条件转换成位置高度线,从而将难以分析的温度变化量Δt直观地显示出来,便于用公式Q=cmΔt分析比较,得出结论,避免了大量的数学推导过程.

