基于经历教学的“二元一次方程组的应用”教学及其分析

    

    

    

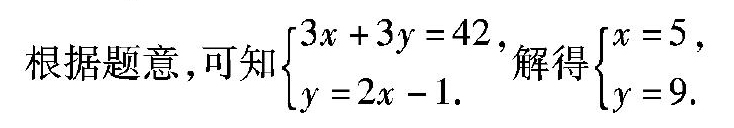
    摘 要：课堂教学过程是学生主动经历的教学活动.学生一步步经历教材预习、知识探索、问题解决、结论概括、体系构建.体现课堂是培养学生核心素养的活动.学生的经历不仅在认知上提升知识构建，而且在过程与方法上提升处理问题的能力，甚至在情感与价值观上建立实践与坚持的品质.

    关键词：经历教学;教学分析;学生经历

    作者简介：金明阳（1987-），男，浙江绍兴人，本科，中学一级教师，研究方向：中学数学课程教育教学研究.

    1 背景介绍

    在课堂改革的教学实践中，经历教学是学生能亲历亲为、亲自感受一些现象、事情、活动、情感等一种教育理念及其教育行为方式.在课堂中教师通过丰富的情境设置，多样的教学活动，不同的教学手段引导学生主动参与课堂，经历知识的发生、发展、延伸、拓展的过程，并在此过程中不仅获得知识的掌握与运用，而且还可培养学生的数学素养.

    本文以浙教版《数学（七下）》“2.4二元一次方程的应用”第一课时为载体，以课堂教学中存在学生对题目束手无策，课后做题不知所措等一系列问题为思考，从而反思到教学中学生的“经历”知识的认知不到位，对运用知识的能力不够.鉴于此，笔者在反复深究学生思维层次与教学目标中，基于经历教学的方式，对这堂课再次设计与改进.以下是简录部分教学过程.

    2 教学实录

    2.1 新知探究中经历知识的产生

    问题1 一水坝的横截面是梯形，它的面积为42m2，高为6m，下底比上底的2倍少1m，则上底和下底的长各是多少米？

    生1：设上底为x米，则下底为（2x-1）米.

    根据题意，可知3x+3（2x-1）=42.

    解得x=5，下底=2x-1=9米.

    答：上底为5米，下底为9米.

    师：这是很好的方法，谁来给大家解？

    生2：如果设上底为x米，从“下底比上底的2倍少1m”找到突破口，下底为（2x-1）m，然后根据面积列出方程.

    师：好，我们继续思考这有几个未知量？有没有其他方法？

    生3：两个，所以可以设两个未知数.设上底为x米，下底为y米.

    根据题意，可知

    3x+3y=42，y=2x-1.解得x=5，y=9.

    答：上底为5米，下底为9米.

    师：我们来比较一下这两种方程.

    生4：第一种思维方式很容易想到.

    生5：第二种好，思维比较简洁，列方程组不用考虑哪个未知量设元.

    生6：通过计算说明，二元一次方程组的解决是“走向”一元一次方程来解决，各有各的优势.

    师：总结，另外提出思考：设下底为x米，又该怎么做？

    设计意图 （1）让学生经历“用”——学生随着题目的思维而调动，看到“下底比上底的2倍少1m”，学生直接是一元一次方程的方式解决，这需要肯定.数学的教学就是复杂问题简单化.本节教学点是用二元一次方程组的应用经历来解决问题，产生了学生思维与教学设计的“矛盾”，这时需要去引导，便设置：问题中有几个未知量？也可以设几个未知数？从而恰到好处地引出新知主题.

    （2）让学生经历“解”——二元一次方程组的解决是转化到一元一次方程，转化中包含着两种方式，即代入消元与加减消元.注重过程的经历是让学生明白本质，从而更好运用.

    （3）让学生经历“思”——教师设置的问题的导向基于学生经历与教学目标相结合，对“一题一总结”的方式，有利于学生在经历中加深感受，在总结中回味无穷.

    （4）让学生经历“再思考”——教师总结与提出另一种思路，让学生体会多种方法解决这类问题，拓展学生思维.

    2.2 新知历练中经历知识的发展

    问题2 游泳池中有一群小朋友，男孩戴藍色游泳帽，女孩戴红色游泳帽.如果每位男孩看到蓝色与红色的游泳帽一样多，而每位女孩看到蓝色的游泳帽比红色的多1倍，问男孩与女孩各有多少人？

    部分学生一看问题已开始做题，另外部分学生仍在积极思考，前者经历了方程组列出与解答，初步已有了处理问题的经历，这时让学生总结这“经历”的过程，得出解决问题的步骤.对于还无法解答的学生，教师及时干预学生思维，产生“经历”过程，从而解答问题.设置下列问题.

    思考：（1）问题中所求的未知数有几个？

    （2）有哪些等量关系？

    （3）怎样设未知数？可以列出几个方程？

    （4）可否仅设一个未知数？用一元一次方程来解决？效果怎样？

    （5）想一想，上面整个思考过程中，你经历了哪些问题解决的基本步骤？

    师：谁来回到问题（1）？

    生7：有2个，男孩人数、女孩人数.

    师：好，精准“定位”了，那么，问题（2）呢？

    生8：①男孩人数-1=女孩人数;②男孩人数=2（女孩人数-1）.

    师：这是最关键一步，在问题中提炼等量关系.那问题（3）呢？

    生9：可设男孩x人，女孩y人，则由题意得 x-1=y，x=2y-1，解得x=4，y=3.

    师：那问题（4）呢？

    生10：可设男生有x人，则女生的人数有（x-1）人，则由题意得，x=2（x-1），解出x的值即可.

    生10：在列出方程组时有点不确定，在算出答案后与刚才的方法算出的答案一样，才肯定.

    师：这的确是解决问题的最好“经历”，有时候寻找解问题的路很多不确定，甚至迷茫中潜行，但在“未知”中寻找正确之路，这种“坚持”值得学习，此类问题，反而觉得“二元一次方程组解决问题”比“一元一次方程解决问题”简单多.能否归纳出解决问题的步骤？

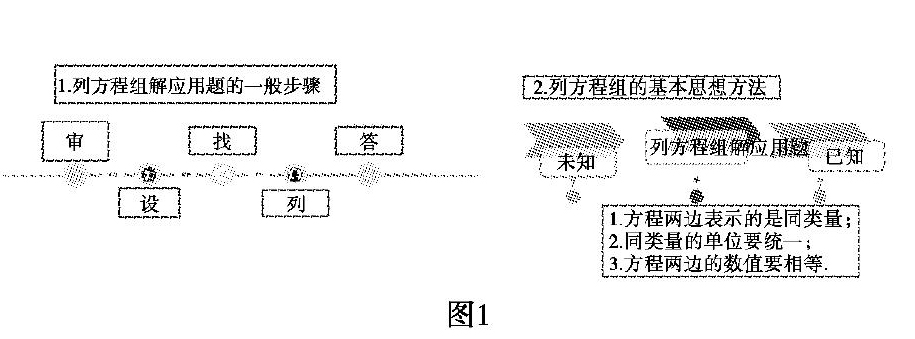
    生12：列方程组解应用题的一般步骤：审→设→找→列→解→答.

    师：非常好，总结的板书如下：

    設计意图 （1）让学生经历“模仿”——当问题所求的未知数有两个时，用字母来表示未知数往往比较容易列出方程.要注意的是必须寻找两个等量关系，列出两个不同的方程，组成二元一次方程组.

    （2）让学生经历“充实”——学生对问题（4）（5）的讨论最激烈.学生的思维从单一的方法解决问题转向多维度、多方法解决问题.

    2.3 题型演练中经历知识的拓展

    问题3 用如图2中的长方形和正方形纸板作侧面和底面，做成如图 3的竖式和横式两种无盖纸盒.现在仓库里有1000张正方形纸板和2000 张长方形纸板，问两种纸盒各做多少个，恰好将库存的纸板用完？

    师：做一个竖式纸盒需要几张长方形纸板和正方形纸板？做一个横式纸盒呢？请填写下表.

    生一起：设做竖式纸盒x个，横式纸盒y个.根据题意得x+2y=1000，4x+3y=2000，解得x=200，y=400.经检验，这个解满足方程组，且符合题意.

    答： 做竖式纸盒200个，横式纸盒400个，恰好纸板用完.

    变式1 如果上题中的条件改为仓库里有正方形纸板500 张，长方形纸板1001张，那么能否在做成若干支所说的两种纸盒后，恰好把库存的纸板用完？说明你的理由.

    变式2 对于变式1的纸板张数，不能完全恰好用完，那么在节约的前提下，如何组合可以做出更多的盒子？说说你的理由.

    变式3 将问题3中的条件改为：正方形纸板有a张，长方形纸板有b张，若恰好把这些纸板用完，请问a，b应满足怎样的关系？

    变式4 将问题3中的条件改为：库存长方形纸板2000张，正方形纸板若干张，那么，要做成竖式纸盒和横式纸盒共600支，且恰好把库存纸板用完，需要正方形纸板多少张？

    变式5 将问题3中的条件“无盖”改为“有盖”.其他条件不变，此题是否有解？如果无解，怎么处理？说说你的想法.

    设计意图 （1）这环节的问题3 的设置让学生经历知识的延伸与拓展，问题的演变本质是不变的，问题3采用列表的方式，让学生的“经历”更加充实与明了，这样往往比较容易列出方程.要注意的是必须寻找两个等量关系，列出两个不同的方程，组成二元一次方程组.

    （2）以“问题串”的形式开展合作交流解决问题，让学生经历更加充实、具体，把课堂真正地还给学生，在“经历”中，提升学生的思维能力和合作交流能力.

    3 教学分析

    3.1 教学过程分析

    本节课的教学重点是让学生经历和体验用方程组解决实际问题的过程，抓住实际问题的等量关系建立方程组模型.教学难点是在探究过程中分析题意，由相等关系正确地建立方程组，从而把实际问题转化为数学问题.教学中，为了突破重难点，主要让学生经历独立思考、自主探索、合作交流、估算验证等学习方式，在思考、交流等数学活动中，养成严谨的思维方式和良好的学习习惯，在解决这些实际问题中，体现了以学生发展为本，让学生积极参与并且有效参与.

    3.2 教学后续思考

    3.2.1 “例题经历”分析

    学生解一系列的“变式”题“经历”体验，即学即用，能想出列方程组的方法，甚至学生之间相互出题，这是实施方案中的最大成功.“经历”体会方法多，方法好，扩展了学生的思维，从而树立学习的信心，激发学习的积极性，让学生真正成为课堂的主人.

    数学是一门精确的学问，也是一门发散的学问，如在“变式”的最后一问中，对这些孩子具有跳跃性与开放性，促使学生深度思考.教师应该更多地引导与积极鼓励学生发散思维，抛开固有模式，充分体现学生个性化能力.

    3.2.2 “变式题经历”思考

    对于变式的拓展也可从方程组出发，让学生编写应用题，反角度去思考与拓展，让知识经历从“形”到‘体，又经历从“体”到“形”.这样设计是不是更完美一些，学生编题不是一件轻而易举的事情，编写的有层次、有深度、有思考，更加可以体现学生的思维深度与广度，精心构思更是一种高级的思维能力.

    学习即经历，学生面对数学问题，学会用简单的方式解决就是最好的学习效果.数学课标中要求发展人人学有价值的数学，学生“经历”活动即是一种“价值”的教学.这样的经历教学，让学生真正实现自我价值，真正地培养学生解决问题的能力，不仅是知识上的螺旋式提升，而且更是思维提升与能力上的价值体现.

    参考文献：

    [1]中华人民共和国教育部.全日制义务教育数学课程标准（实验稿）[M].北京：北京师范大学出版社，2001.

    [2]林霖. 基于过程教育的“代数式的值”的教学及其分析[J]. 中小学数学（初中版），2018（06）：59-62.

    [3]丁义国. “经历教学”：教给学生“带得走”的知识[J]. 教育研究与评论（中学教育教学）;2017（12）：44-47.

    [4]蔡正华. 聚焦数学素养：让学生拥有带得走的能力[J]. 数学教学通讯，2017（35）：22-23.

    （收稿日期：2020-02-04）