平面图形“高”的学习困难分析与教学尝试

    黄德发

    

    

    

    摘要：在教学中发现，许多学生对“高”的理解存在困难，主要源自生活经验与数学内涵之间的冲突。在三角形高的教学中，教师要注意建立数学与生活的联系，找准知识生长点，注意加强比较，触及概念本质，实现理解再提升，促进深度学习。

    关键词：小学数学 ?教学尝试 ?平面图形 ?高

    人教版四年级上册平行四边形和梯形单元，涉及平面图形“高”的知识。许多学生对“高”的理解不够透彻，在辨认和作图中会出现很多错误。在与其他教师的交流中，笔者发现这不是偶然现象，必定有深层次的原因，有必要探根求源，找到破解方法，重塑学生对“高”的认识。

    一、探寻“高”的意义，寻求问题根源

    （一）何为高？

    在日常生活中，我们说这个物体有多高，一般都是指物体的高度，即顶部到地面的距离。这些生活经验使学生很容易辨认竖着的高，而对其他形式的高难以理解。显然，学生把生活中的高与几何图形的高混为一谈了。因此，学生对几何图形的高存在认知困难，存在着深厚的生活根源。

    （二）何为平面图形的高？

    在小学阶段，我们学习的高主要指的是平行四边形、梯形和三角形的高。人教版教材对平行四边形的高是这样说的：从平行四边形一条边上的一点向对边引垂线，这点到垂足之间的线段就是平行四边形的高。对于梯形的高教材上只给了一幅图，让学生直观感知，其实与平行四边形的高类似。

    四年级下册对三角形的高是这样定义的：从三角形的一个顶点到它的对边作一条垂线，顶点到垂足之间的线段叫作三角形的高。

    不难发现，两条平行线之间的垂线段就是平行四边形或梯形的高，顶点到对边的垂线段就是三角形的高。高的本质其实就是点到直线的垂线段。

    教材中对“高”概念的描述，学生是不容易理解的。要想理解“高”的概念需要“顶点”“对边”“垂线”“垂足”等众多概念为支撑，而这些概念也是刚学习的，要理解“高”的概念实在是个挑战。

    （三）生活中的高与平面图形的高有何联系和区别？

    1.联系紧密。平面图形的高是高的本义的延伸，生活中通常所说的“高”，一般是指与水平线垂直的线段的长度，这为学生理解平面图形竖直方向的“高”提供了便利。

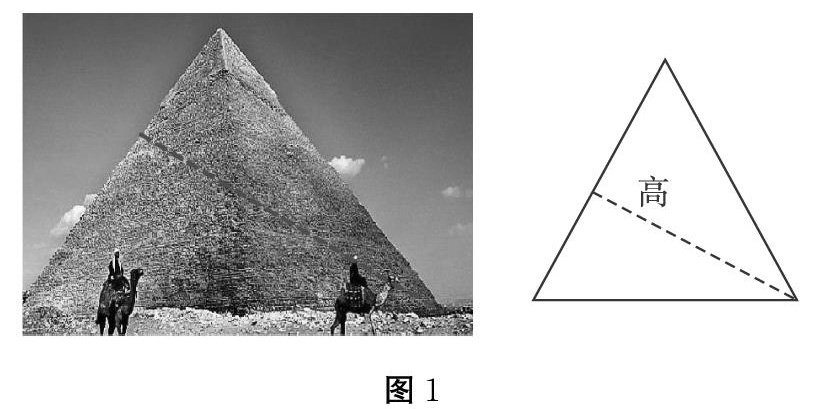
    2.区别明显。首先，平面图形的“高”一般指的是垂线段，这一点和生活中所说的“高”有所区别，但并不明显，因为平面图形的“高”也会用来表示垂线段的长度。其次平面图形的高，并不一定是竖直的，除非它的底是水平的。平面图形的高是与底垂直的，而底可以与水平方向成任何角度。这就与学生的生活经验产生冲突，进而产生学习困难。如图1，右图虚线是三角形的高，而左边图中的虚线则和金字塔的高并无关系。这就体现了数学源于生活却高于生活。

    图1通过以上三个问题的分析，我们不难发现，除了概念表述本身难以理解，学生对高的认识困难主要源自生活经验与数学内涵之间的冲突。

    二、结合三角形高的认识，重建“高”的概念。

    基于以上的分析，笔者认为，“高”的学习，既要扎根于现实生活，也要立足于数学内涵。因此，在三角形高的教学中，我把它摆在了一个非常重要的位置。

    三角形的高相对于平行四边形和梯形的高，更具有复杂性，三角形有三条不同的高，钝角三角形有形外高，直角三角形有两条高与边重合。如何突破这些难点，让学生深刻理解？教学中可以从以下三个方面进行了有效尝试。

    （一）建立联系，找准知识生长点

    “高”的概念来源于生活，为了建立联系，教学中从学生熟悉的“量身高”引入，有效地激活学生的生活经验。

    课堂实录：

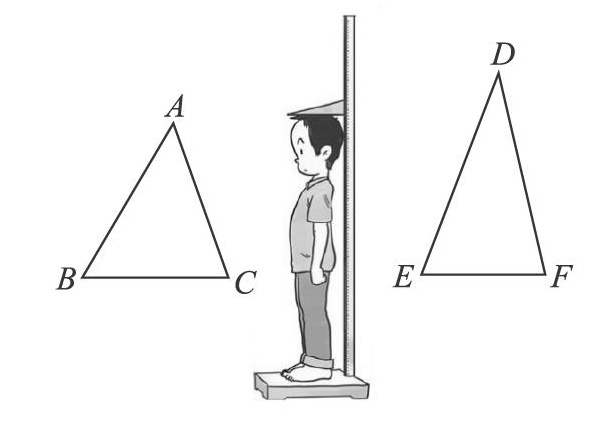
    师：三角形ABC与三角形DEF是好朋友，有一天他们要去量身高，同学们你们量过身高吗？

    生：量过。

    师：你们是怎么量身高的呢？出示下图

    生：站直，上面的标尺要放到头顶上。

    师：那么，这个同学的身高是从哪到哪呢？

    生：从头顶到脚底。

    师板书：头顶 脚底 站直了

    在测量身高的情境中，学生感受到头顶与脚底之间的垂直长度就是身高，为感知图形的高初步建立与生活的联系。

    课堂实录：

    师：三角形ABC要去量身高，想一想，他的身高应该是從哪儿到哪儿呢？

    生：从点A到BC。

    师：从点A到BC有很多种方法。（师用手势比画多条线路）到底是哪一条呢？

    生1：竖直的那一条。

    生2：与BC垂直的那一条。

    师：你能画出它吗？应该怎样画？

    生：用三角尺直角去画。（学生画出这条线）

    师：用自己的话说一说，这是怎样的一条线？

    生：从顶点A到对边BC画的一条垂线。

    师板书：顶点 对边作垂线

    师生小结高的概念，并说明：这条对边就像人的脚底一样，我们称之为“底”。

    通过激发生活经验，学生建立了头顶与顶点，脚底与对边之间的关联，建立了数学与生活的联系，初步感受到高的一般形态。

    （二）加强比较，丰富高的表象

    平面图形的高与生活中的高有显著的区别，由于学生经验的不足，对高的认识很容易停留在“竖直”经验上，为此，必须进一步加强与生活中高的比较，丰富几何图形高的表象。

    课堂实录：

    在比较三角形ABC与三角形DEF身高之后，创设如下情境：

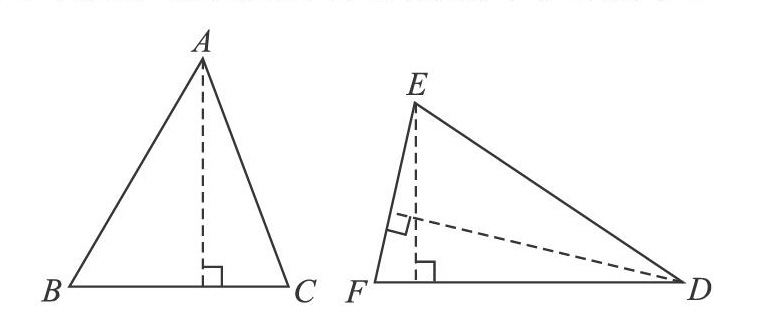
    师：三角形DEF比身高获胜，高兴得又蹦又跳，一不小心，脚下一滑，摔倒了（出示下图），三角形ABC看见了，笑着说：哈哈，你的个子变矮了。

    师：同学们，这时，三角形DEF的个子是多高，你能指出来吗？

    学生指出三角形的高，课件用虚线呈现。

    师：为什么这也是三角形的高呢？

    生：因为这是顶点E到对边FD的距离。

    师：那么，刚才我们从D点画出的那条线还是三角形的高吗？

    生：不是

    师：说出你的理由。

    生：因为他不是竖直的

    师：“高”一定要竖直的？

    生：不一定，它应该还是三角形的高，因为刚才老师说了，从顶点到对边作垂线，这条垂线段的长度就是他的高。D是三角形的顶点，EF是它的对边，而且这条线垂直EF，所以它也是三角形的高。

    师：你们认为呢？（经讨论学生逐渐认同）

    师：当自己不太确定的时候，我们可以根据它的定义来判断。从三角形的一个顶点向它的对边作垂线，顶点到垂足之间的线段就是它的高。符合这个定义它就是高。从这里我们也可以看出，高有时候不是竖直的，和我们身高不一样，和我们生活中说的物体的高度也是有区别的。

    师：想一想，一个三角形有几条高呢？为什么？

    对高的认识，我们不能仅停留在生活经验上，既要从生活中来，又要高于生活，通过这样情境的创设，不断丰富“高”的表象，学生对高的认识达到了新的高度，有效地避免了“竖直”经验的干扰，学会理性地从数学概念来进行推理判断，培养学生的理性精神。

    （三）触及本质，实现再提升

    画“高”其实就是过直线外一点作已知直线的垂线，但由于受到三角形另外两条边的影响，学生容易出现这样那样的错误，因此，我们把高的学习与旧知联系起来，使学生进一步感受到高的本质，实现理解的再提升。

    课堂实录：

    依次出现下面两个问题，让学生独立解答。

    问题1：小明家的旁边有条河，小明爸爸想修一条路到河边，怎样修最近呢？你能画出这条路吗？

    问题2：小红家的旁边也有一条河，小红家到这条河有两条路，不过，她爸爸觉得这两条路都比较远，想修一条最近的路，她該怎么修呢？

    完成后，引导学生讨论。

    师：在画这两条小路的过程中，你有什么发现吗？

    生1：都要画垂线，与小河垂直。

    生2：他们的画法一样。

    生3：第二个图中，原来的两条路和小河构成一个三角形，这条最近的路就是三角形的高。

    生4：三角形的高和点到直线的距离是一样的。

    师：说得真好，通过刚才的讨论，我们知道高其实并不神秘，他就是以前我们所认识的点到直线的垂线段。因此，在画三角形高的时候，有时可以忽略另外两条边。

    师：通过学习，你认为为什么要研究三角形的高呢？

    生1：因为我们知道，点到直线的所有连线中垂线段最短，因此三角形的高就是顶点到对边最短的一条线。

    生2：这条线最短，很特殊，值得研究。

    师：“高”正因为它的特殊性，在解决许多图形问题中发挥着重要的作用。因此，我们大家一定要学好它，用好它。

    建立新旧知识之间的联系，能使学生建构更加完整的知识体系，有利于学生站在新的高度重新审视所学知识。

    总之，数学产生于生产实践。在教学中，我们既要抓住它们之间的联系，也要注意它们之间的区别，从更加理性的角度找到学生学习数学知识的生长点，把握数学概念的内涵和本质，让学生在思辨的过程中得到思维的发展。