?数学实验不要抄近路
朱崇友

摘? 要 在小学数学教学中,实验是不可或缺的一种教学方式,在动手操作和动脑思考相结合的过程中,可帮助学生实现自主知识构建。但实验教学不能一味地抄近路,有时适当地绕远,可更好地保证教学生成。以“多边形的内角和”教学为例,对小学数学实验教学进行相关研究探索。
关键词 数学实验;多边形;内角和;小学数学;教学改革
中图分类号:G623.5? ? 文献标识码:B
文章编号:1671-489X(2020)07-0118-03
1 前言
伴随教学改革的不断深入,传统灌输式的教学方式受到质疑,而符合新课程理念,将动手与动脑结合在一起的实验教学方式则受到教师的青睐与欢迎。但实验教学切记不可一味抄近路,要将发展学生的逻辑推理能力作为核心;有时多些等待,可更好地发挥实验教学的优势。
2 课堂回放:抄近路的数学实验
“多边形的内角和”是学生在小学阶段学习的一个十分重要的数学知识,实验与此节课程是极为契合的。如教师可通过实验的方式,引导学生依次探究长方形和任意四边形的内角和,从而让学生对多边形的内角和规律作出总结,实现主体知识构建的目的[1]。在以往的教学过程中,很多教师为了追求高效,保证教学进度,总是一味抄近路,反而造成适得其反的教学效果。下面笔者以“多边形的内角和”实验教学课程为例,对抄近路的课堂进行回放。
师:过往我们曾经学习过三角形内角和知识,知道三角形的内角和为180°,那么多边形的内角和又是怎么样的呢?请大家通过实验探究的方式,总结多边形内角和规律。
教师为学生展示长方形、任意四边形、五边形及六边形的图片卡纸。
生:我对五边形的内角和进行了探究,主要是采用分割的方式,将五边形分成三个三角形(如图1所示)。通过过往学习的知识,我知道三角形的内角和为180°,因此可以得出五边形的内角和为180°×3=540°。
师:首先要对你勇于探索的精神表示赞扬,但对此也有一些质疑和疑问。若是按照你的思路方法,是不是可以将五边形进行这样的分割(出示图2和图3)?这样五边形的内角和岂不是等于720°或900°?
生1:我不认同这个观点,因为这些三角形的内角与原来的五边形内角相比,要多出一些角。
生2:我觉得老师这样分割也是可以的,但是可以先把分出来的三角形内角和合在一起,然后从中剔除多余的角,这样就不冲突矛盾了。
师(提问生2):你能够上台指出图2和图3哪些角是多出来的吗?并请做出相应的标记。
师(生2上台指明后):你做得非常好,但是老师还是想问大家,比较上述几种分割方法,你们更喜欢其中的哪一种?
生:我喜欢图1的分割方法,因为这样分割不仅操作简便,而且计算起来也非常简单。
师:你说得非常对,在探究多边形内角和时,对多边形进行划分一定要秉持尽量不要有多出来的角的原则。因此,老师建议同学们按照图1的方法进行分割,从一个顶点出发进行分割,依次连接和它相对的五边形的顶点,这样操作起来比较简便。那么接下来请大家按照这样的方法,继续进行六边形、七边形、八边形的内角和探索。
……
3 课堂重构:“绕远路”的数学实验
在上文中,笔者介绍了抄近路的数学实验教学,下面进行课堂重构,对“绕远路”的数学实验进行分析,主要是在呈现图1、图2、图3等不同分法后所作出的课堂重构。
师:图1、图2、图3三种方法都是将五边形分成了三角形,可是为什么最终分出的三角形个数不同?那么最终得到的结果岂不是互相冲突吗?
生1:因为图1是从一个顶点出发进行分割的,而图2是从底边上的一个点出发进行分割的,图3是从图形中间的点出发进行分割的。
生2:图2和图3虽然将五边形依次分割成了四个三角形和五个三角形,但是其中有些三角形的角是不能算作五边形内角的。
师:你们总结得非常好,那么有哪些角不能算作五边形的内角呢?
生2走上讲台,标记出图2中不能算作五边形内角的四个角。
師:那么你们知道如何根据图2的分法,求得五边形的内角和吗?根据图3的分法又怎样求五边形的内角和呢?
生1:根据图2的分割方法,将该五边形划分成四个三角形,得到内角和的度数为180°×4=720°。而其中有四个角不能算作五边形的内角,这四个角又处于一个平角内,其和为180°,因此,五边形内角和为720°-180°=540°。
生2:根据图3的分割方法,将五边形划分为五个三角形,得到内角和的度数为180°×5=900°。而其中有五个角是不能算作五边形内角的,这五个角处于一个周角内,其和为360°,那么五边形内角和为900°-360°=540°。
师:你们做得非常好,通过这样的分析也可以发现,尽管大家采用的分割方法不同,但最终得到的结果却是一样的,都可以得出五边形的内角和为540°,那你们觉得这几种分割方法哪一种最好呢?
大部分学生都表示喜欢图1的分割方法,因为这样划分简单、直接,不用进行额外的计算。
师:既然大家都比较喜欢图1的划分方法,那你们认为这种方法的优点在哪呢?
生1:图1的划分方法,从五边形的一个顶点出发,依次连接和它相对的五边形的顶点。
生2:图1的划分方法分割出来的三角形内角合在一起,正好等于五边形的内角和,不多余出其他的角。
师:虽然大部分的同学都认为图1的划分方法很好,但是老师还是希望每个同学都能够遵从自己的意见,按照自己喜欢的方式,继续对六边形、七边形、八边形的内角和进行探究。
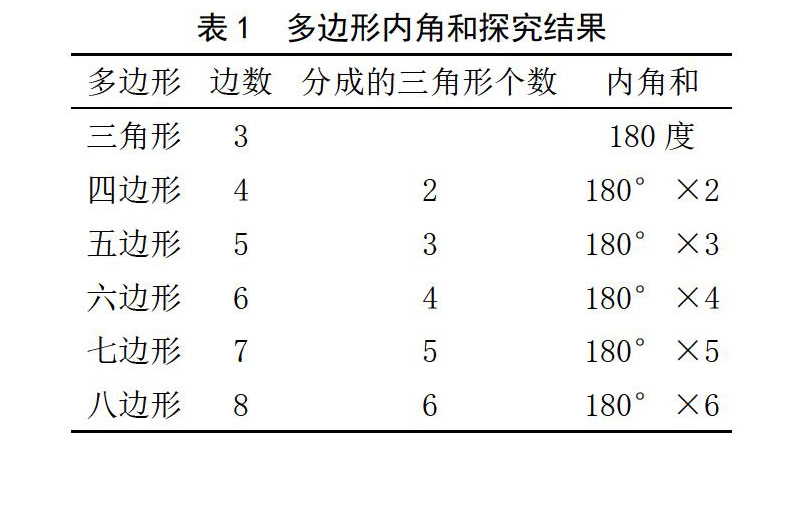
学生按照自己的方法各自操作、计算、实验,在探究活动结束后,对探究出的结果进行整理,具体详见表1。
师:根据得出的结果,你们认为计算多边形的内角和的方式有哪些共同特点?
生1:都是通过180°与一个数相乘得到的结果。
生2:和180°相乘的数就是多边形划分时分成三角形的个数。
师:谁知道分成三角形的个数與多边形的边数有哪些关系?
生3:分成三角形的个数等于多边形的边数减2。
师:要是按照你们的思路,那么当多边形的边数为n
时,如何计算它的内角和呢?
生4:可以表示为180°×(n-2)。
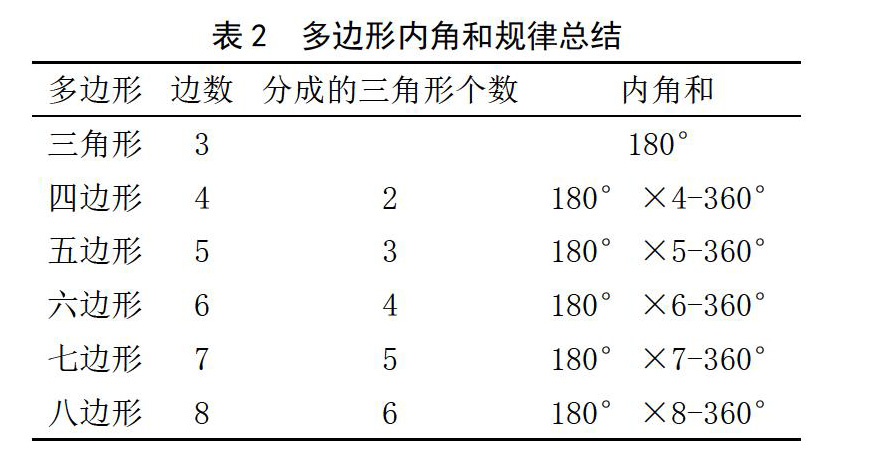
师:你们总结得非常好。按照你们的计算方法,老师也进行了总结,如表2所示。你们能看懂该表中的数据信息吗?
生:我可以看懂,也就是说该多边形是几边形,就将其分成几个三角形,然后先用180°与分成的三角形个数相乘,再减去360°。
师:看来这位同学看懂了,那么其他同学也看懂了吗?你们可不可以根据老师出示的表格数据,进一步对多边形内角和计算公式作出总结?
生:可以表示为。
师:你总结得非常好,但是老师还是有一个疑问:上面曾有同学提到用180°×(n-2)进行多边形内角和计算,现在又有同学提出用180°×n-360°进行计算,能够保证两个公式得出的结果一样吗?
生1:得到的结果是一样的,因为180°×n-360°的360°,正好是两个三角形的内角和的度数,所以计算出的结果是一样的。
生2:我也认为得到的结果是一样的,主要是根据乘法分配律:180°×(n-2)=180°×n-180°×2=180°×n
-360°。
师:你们总结得非常好,虽然这两个计算公式看上去不一样,但是计算的本质却是一样的。今后在进行多边形内角和计算时,你们可以结合自己的方法习惯,自由选择计算方法。
4 总结反思:数学实验,切记不可抄近路
上述笔者提及的两种教学方法,都是典型的数学实验教学,具有开放性强、思考探究空间大的特点,有利于学生主体构建知识。由于实验教学容易出现时间不够用的情况,为避免对教学进度造成影响,在回放的实验教学1中,教师代替学生直接进行规律总结,将“从一个顶点出发,依次连接和它相对的多边形的顶点”的实验探究思路告知学生,这样的实验教学显然是走了捷径、“抄了近路”,学生后面的实验探究也貌似非常顺畅,只要依照教师的思路,就可以顺利地展开实验探究。但是这样抄近路的数学实验教学缺点也是非常明显的,就是没有尊重学生的主体作用,思路源自教师的灌输,而不是通过学生自主思考获得的。这样的教学只是把班级中多个学生的脑袋变成一个脑袋,让学生用一种方法去探究解决同一个问题,极大地限制了学生的思维,不仅阻碍学生探究学习兴趣的激发,也不利于培养学生独立思考的习惯,影响数学实验作用的发挥。
而在重构的实验教学2中,看起来是多了一些弯路,绕了远路,但实际在这个过程中却尊重了学生的主体地位,为学生留出求异思维和创新意识的空间,可以更好地让学生体会“尽管出发点不同,但是条条道路都可以通罗马”,学生的数学学习思维会变得更加开放[2]。同时,在重构的数学实验2中,学生根据规律自主概括出两种计算多边形内角和的公式,并且在教师的启发下进一步思考了这两个计算公式是不是可以得到一样的计算结果。在这样的实验教学中,引导学生从运算意义和运算率角度出发,对计算公式作进一步探究,将规律探究提升了一个台阶,上升到新的高度层次,得到更好的实验教学效果。
通过上述两个实验教学对比得出这样一个结论,即在小学数学实验教学中切忌抄近路,只要学生的逻辑推理能力得到培养,即使是多费了功夫,走了远路也无妨,这是小学数学教师今后开展实验教学时要谨记的。
5 结语
实验作为教学改革中所提倡的一种教学方式,在小学数学教学中极具应用价值。但应引起小学数学教师注意的是,数学实验不可一味抄近路,要多一些等待,多尊重学生的想法,确保学生的逻辑推理能力得到培养。这样的教学看似绕了远路,却可实现意想不到的教学效果,有效提升学生的创新思维能力。
参考文献
[1]王小波.高观点,让数学教学更多元:以“多边形的内角和”一课为例[J].小学教学参考,2019(8):7-8.
[2]李霞,徐铎厚.发展核心素养的数学教学设计构想:以“多边形及其内角和”为例[J].教学月刊·中学版:教学参考,2017(6):7-9.

