此题条件不充分
汪少辉
人民教育出版社义务教育课程标准实验教科书八年级下册p.121页习题19.3第七题如下:
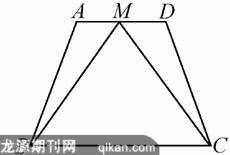
图1
如图1,四边形ABCD中,AD∥BC,M是AD的中点,MB=MC,求证四边形ABCD是等腰梯形. 根据此题的条件,我们能否得到这个四边形为梯形呢?看如下证明.
证明 因为MB=MC,所以∠MBC=∠MCB,因为AD∥BC,所以∠AMB=∠MBC,∠DMC=∠MCB,所以∠AMB=∠DMC,在△AMB与△DMC中,AM=DM,∠AMB=∠DMC,MB=MC,所以△AMB≌△DMC,所以AB=CD.
到此,若加上AD∥BC是否就可断定四边形ABCD是等腰梯形呢,显然不可. 我们知道要得到一个四边表是梯形,必须知一组对边平行,另一组对边不平行. 在AD∥BC的前提下,AB与CD是否不平行,根据题目的条件,显然不知道,因此我们不能判断这个四边形就是梯形. 更谈不上它是一个等腰梯形了.
让我们看一看下面的例子:
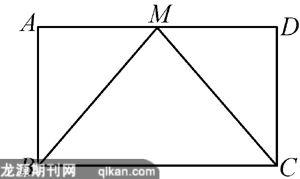
图2
如图2,现将原题中的四边形ABCD改成矩形ABCD,其它条件不变,是否也能得到AB=CD呢?
证明 因为MB=MC,所以∠MBC=∠MCB,因为AD∥BC,所以∠AMB=∠MBC,∠DMC=∠MCB,所以∠AMB=∠DMC,在△AMB与△DMC中,AM=DM,∠AMB=∠DMC,MB=MC,所以△AMB≌△DMC,所以AB=CD.
我们是否就说四边形ABCD是梯形呢,显然是不可能的,由此看来,课本上的这个题的条件是不充分的.
人民教育出版社义务教育课程标准实验教科书八年级下册p.121页习题19.3第七题如下:

图1
如图1,四边形ABCD中,AD∥BC,M是AD的中点,MB=MC,求证四边形ABCD是等腰梯形. 根据此题的条件,我们能否得到这个四边形为梯形呢?看如下证明.
证明 因为MB=MC,所以∠MBC=∠MCB,因为AD∥BC,所以∠AMB=∠MBC,∠DMC=∠MCB,所以∠AMB=∠DMC,在△AMB与△DMC中,AM=DM,∠AMB=∠DMC,MB=MC,所以△AMB≌△DMC,所以AB=CD.
到此,若加上AD∥BC是否就可断定四边形ABCD是等腰梯形呢,显然不可. 我们知道要得到一个四边表是梯形,必须知一组对边平行,另一组对边不平行. 在AD∥BC的前提下,AB与CD是否不平行,根据题目的条件,显然不知道,因此我们不能判断这个四边形就是梯形. 更谈不上它是一个等腰梯形了.
让我们看一看下面的例子:

图2
如图2,现将原题中的四边形ABCD改成矩形ABCD,其它条件不变,是否也能得到AB=CD呢?
证明 因为MB=MC,所以∠MBC=∠MCB,因为AD∥BC,所以∠AMB=∠MBC,∠DMC=∠MCB,所以∠AMB=∠DMC,在△AMB与△DMC中,AM=DM,∠AMB=∠DMC,MB=MC,所以△AMB≌△DMC,所以AB=CD.
我们是否就说四边形ABCD是梯形呢,显然是不可能的,由此看来,课本上的这个题的条件是不充分的.

