三种几何变换的主要作用
在现行的初中数学课本中[1],给出了平移、旋转和轴对称(即翻折)三种几何变换. 它们都是不改变图形的形状和大小,只改变图形位置的变换. 它们在中学数学教材的平面几何理论体系中具有重要作用. 下面列举几个主要作用.
1 为判别相同的图形提供依据和方法
在课本七年级上册,关于画出正方体的11种不同的表面展开图,必须涉及到什么是相同的图形;在七年级下册,关于三角形全等的定义,又必须涉及什么样的两个三角形是相同的三角形;等等. 在没有讲任何图形全等的相关定理前,需要选用过渡性“依据”去判别两个相同的图形,并且还要求这种过渡性理论“依据”必须易于学生理解和操作方法简便. 笔者认为平移、旋转和翻折变换是最合适的选择对象.
把一个任意的平面图形通过平移、或旋转、或翻折变换,得到的新图形一定是与原图形全等的图形. 虽然初中学生对它给出证明是困难的,但是用具体的平面图形采用平移、旋转和翻折变换后,它们不会改变原图形的形状和大小的事实可以说明它. 既然可用直观方法说明上述客观事实,那么就以“教学公理”形式来处理,把一个平面图形通过平移、或旋转、或翻折变换后,能与另一个平面图形完全重合时,这样的两个平面图形就可以叫做相同图形或全等图形. 因此,对画出的两种正方体的表面展开图是否为相同图形,就可以依据这三种几何变换进行“图形搬迁”的方法来判断. 若搬迁后的两个图形能完全重合,则它们就是相同图形;若用平移、旋转和翻折的搬迁方法,总是不能使两个图形完全重合,则它们就不是相同图形. 对三角形全等来说,课本给出了三角形全等的判定定理. 只要能确定两个三角形有符合相关的三角形全等判定定理的条件,就可以获得这两个三角形全等的结论. 这可以避免用三种几何变换进行图形搬迁方法确定两个图形全等的冗长表述和图形搬迁的麻烦. 解几何题时,常要寻找两个静态的平面图形间的相同关系,如果能通过动态过程确定两个静态的平面图形是怎样产生的,那么常常可以提供重要的解题信息和方法. 这说明三种几何变换不仅是构造两个图形全等的重要工具,而且它们是不可忽视的证明两个图形全等的重要的解题思考方法. 利用运动变化观念去认识事物符合辩证法.
2 为识图和构图提供指导思想和操作方法
在课本的七年级下册编排了图形的轴对称变换内容,给出了轴对称图形和图形成轴对称. 在八年级上册再安排了图形的平移和旋转变换内容. 课本以较大篇幅安排了几何变换的应用实例,即把一个“简单”的平面图形,通过平移、旋转、翻折变换,构造出许许多多复杂而美丽的“图案”. 这样既可以丰富学生对图案的美感,又可以从图案的构成方法去认识图案的结构. 特别是对“基本图形”的不同选择,运用不同的变换方法可获得某些相同的特殊图形. 由于“基本图形”的相对性,事物运动变化的多样性,这有利于培养学生的辩证唯物主义的认识观. 课本通过上述指导思想和具体操作方法,结合课本的配套练习,能有效地培养学生的识图和构图的能力.
3 为证明平面几何习题提供重要的动态分析方法
解题的本质是把题目的条件信息和结论信息建立起科学的联系[2]. 解题的表述就是阐述其科学联系的建立过程的具体理由. 在这种意义上说,解(证)几何题就需要不断地变换前后步骤的“形式”或“思想”. 解数学题的灵魂就是“合理变化”. 合理的变化中常会拓展出解题所需要的一片新天地,缺失合理变化时常会在呆滞中一筹莫展. 既然解证几何题需要不断地合理变化,那么解(证)几何题的分析就必须适时运用运动变化的观点和方法.
因为绝大多数“静态”的数学题都是在某种动态环境下,静止于某种特殊情况时的特殊状态,它就像“运动物体”在某一时刻的所拍下的“照片”,所以要把数学题赋予为“灵性之物”,要研究它由谁以怎样的运动方式产生,静止于何时之状. 对于全等图形来说,就需要观察分析图形的平移、旋转和翻折运动,明确数学题中的图形是通过怎样的运动形成. 让相关的图形“动起来”之后,就能突显它们之间特殊的位置关系和大小关系,就容易从中分析捕捉到重要的解题信息和发现解题方法. 例如:
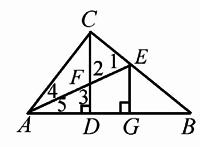
图1
题1 已知:如图1,△ABC,∠ACB=90°,CD⊥AB于D,AE是△ABC的角平分线,AE交BC于E,AE交CD于F, EG⊥AB于G,
求证:CF = EG.
(1)用动态分析方法研究题1构成机理,发现题1的解题信息
①从相关图形旋转考虑
如图1,给定Rt△ABC,斜边AB上的高CD就确定了. 把射线AE绕点A沿逆时针方向从AB旋转到AC时,点E由点B运动到点C,同时点F由点D运动到点C,点G由点B运动到点D,于是CE由BC退缩为点C,CF由CD退缩为点C, 线段EG在平移中由点B逐步“长高”到CD. 因为在此运动中,CE 、CF与EG都是同时开始、同时结束的连续变化的线段,且CE与CF都由长变为短,EG由短变长,它们的长度“最小值”都是零,所以必有CE = EG和CF = EG.
当CE = EG时,又AE是公共斜边,所以Rt△AEC≌Rt△AEG(HL定理),所以∠4=∠5. 此时,AE正好是△ABC的角平分线.
反过来,只要在动态的变化中把“AE是△ABC的角平分线”的特殊情况“静止”下来,那么题1的条件就全有了,并且依据角平分线性质定理,立即可得∠4=∠5,CE = EG(角平分线上的点到角的两边距离相等). 在Rt△AEC和Rt△AFD中,因为∠1与∠4互余,∠3与∠5互余,又∠4=∠5,所以∠1=∠3. 因为∠2与∠3是对顶角,所以∠2=∠3. 所以∠1=∠2,所以CE =CF. 又CE = EG,所以CF = EG.
这种利用某图形旋转建构动态分析,既能说明题1的存在性和这种构造理由,又能探究出题1的一种证明方法,且发现了与结论相关的线段CE是证明本题之关键.
②从相关图形的轴对称考虑
对题1,给定Rt△ABC,斜边AB上的高CD就确定了. 因为AE是Rt△ABC的角平分线,所以∠4=∠5. 又Rt△ABC的直角边AC必小于它的斜边AB,所以把Rt△AEC沿AE翻折180°,所以AC必然落在AB上,从而得到Rt△ABC关于直线AE对称的△AEG. 因为∠ACB=90°,所以EG必垂直AB于G. 这就有了题1的全部条件. 也找到了从“证明三角形全等”入手的解题方法. 易证∠4=∠5,∠ACB=∠AGE=Rt∠,又AE是公共边, 所以Rt△AEC≌Rt△AEG(AAS),所以CE = EG,∠1=∠AEG. 又因为EG⊥AB,CD⊥AB,所以CD∥EG,所以∠2=∠AEG. 又∠1=∠AEG,所以∠1=∠2,所以CE =CF. 又CE = EG,所以CF = EG.
这种利用某图形翻折建构动态分析,既能从新的角度说明题1的存在性和构造理由,又能探究出题1的新的证明方法. 此外,还可以从中收获其他解题信息,例如:由于两个图形关于直线对称,对称点的连线被对称轴垂直平分. 所以AE垂直平分CG,所以CF =FG,CE = EG(线段垂直平分线上的点,到线段两个端点等远). 等等.
③从相关图形的平移考虑
如图1,给定Rt△ABC,斜边AB上的高CD就确定了. 让直线EG从CD开始向右平移到经过点B,让直线FG从BC开始向下平移到经过点D,对应的线段EG和FG都分别由长变短,它们的长度“最小值”都是零,所以必有FG = EG情况存在. 而夹在两平行线之间的平行线段相等,所以有CF = EG. 在此特殊情况下,必有CE = EG,由于有∠ACB=Rt∠,EG⊥AB于G的给定条件,所以AE也正好是△ABC的角平分线. 由于相关的部分图形的对称性,此时点F就在AE上. 这就说明了题1成立,找到了证明CE = EG是证明题1的关键.
(2)用动态分析方法研究题1的关联题,探究变式解题教学方法.
在题1的条件下,由上述分析和推理已知CF = CE = EG,又CF与 EG都垂直于AB,所以四边形CFGE是菱形. 于是把题1改造成题2
题2 已知:如图2,△ABC中,∠ACB=90°,CD⊥AB于D,AE是△ABC的角平分线,AE交CD于F,AE交BC于E,EG⊥AB于G,
求证:四边形CFGE是菱形.
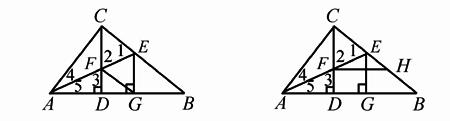
图2
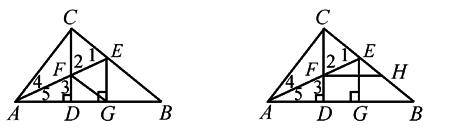
图3
在题1的条件下,由上述分析和推理已知CF = EG,又CF与 EG都垂直于AB,若再作FH∥AB交BC于H,于是可推出Rt△CFH≌Rt△EGB(AAS),从而有CH=EB. 所以有CH-EH=EB-EH,即CE=BH. 于是把题1改造成题3
题3 已知:如图3,△ABC中,∠ACB=90°,CD⊥AB于D,AE是△ABC的角平分线,AE交CD于F,AE交BC于E,EG⊥AB于G,FH∥AB交BC于H,
求证:CE=BH. (或求证CF=BH)
综上所述,在解题教学中探究关联题的变式联系,也常需要对数学题及它们的解答进行动态分析探究.
物质的世界里,事物的运动变化造就了事物间的联系形式具有多样性. 许多事物的“隐蔽”联系形式常需用动态分析方法去探究发现. 从哲学意义上说,“解题”就是不断探究发现“未知世界规律”的过程,因此解题教学要重视关联题的研究,加强变式解题示范,充分发挥三种变换的作用,适时运用动态分析的研究方法去解题.
参考文献
[1] 马复主编.义务教育课程标准实验教科书《数学》 (七年级下册 八年级上册 )[M].北京师范大学出版社,2005.
[2] 邱卫平.建构“选择·探究·发展”的解题教学模式@提高中学数学的解题教学效率[J].数学教育研究,2006,(1).
作者简介 邱卫平 (1953-),男,湖南常德人,中学数学高级教师,特级教师,长期从事中学数学教学与研究,曾参与深圳市中考数学考试说明的编写与修改,多次担任深圳市中考数学命题组长,先后多次担任过中考阅卷组长和阅卷质量检查组长.
1 为判别相同的图形提供依据和方法
在课本七年级上册,关于画出正方体的11种不同的表面展开图,必须涉及到什么是相同的图形;在七年级下册,关于三角形全等的定义,又必须涉及什么样的两个三角形是相同的三角形;等等. 在没有讲任何图形全等的相关定理前,需要选用过渡性“依据”去判别两个相同的图形,并且还要求这种过渡性理论“依据”必须易于学生理解和操作方法简便. 笔者认为平移、旋转和翻折变换是最合适的选择对象.
把一个任意的平面图形通过平移、或旋转、或翻折变换,得到的新图形一定是与原图形全等的图形. 虽然初中学生对它给出证明是困难的,但是用具体的平面图形采用平移、旋转和翻折变换后,它们不会改变原图形的形状和大小的事实可以说明它. 既然可用直观方法说明上述客观事实,那么就以“教学公理”形式来处理,把一个平面图形通过平移、或旋转、或翻折变换后,能与另一个平面图形完全重合时,这样的两个平面图形就可以叫做相同图形或全等图形. 因此,对画出的两种正方体的表面展开图是否为相同图形,就可以依据这三种几何变换进行“图形搬迁”的方法来判断. 若搬迁后的两个图形能完全重合,则它们就是相同图形;若用平移、旋转和翻折的搬迁方法,总是不能使两个图形完全重合,则它们就不是相同图形. 对三角形全等来说,课本给出了三角形全等的判定定理. 只要能确定两个三角形有符合相关的三角形全等判定定理的条件,就可以获得这两个三角形全等的结论. 这可以避免用三种几何变换进行图形搬迁方法确定两个图形全等的冗长表述和图形搬迁的麻烦. 解几何题时,常要寻找两个静态的平面图形间的相同关系,如果能通过动态过程确定两个静态的平面图形是怎样产生的,那么常常可以提供重要的解题信息和方法. 这说明三种几何变换不仅是构造两个图形全等的重要工具,而且它们是不可忽视的证明两个图形全等的重要的解题思考方法. 利用运动变化观念去认识事物符合辩证法.
2 为识图和构图提供指导思想和操作方法
在课本的七年级下册编排了图形的轴对称变换内容,给出了轴对称图形和图形成轴对称. 在八年级上册再安排了图形的平移和旋转变换内容. 课本以较大篇幅安排了几何变换的应用实例,即把一个“简单”的平面图形,通过平移、旋转、翻折变换,构造出许许多多复杂而美丽的“图案”. 这样既可以丰富学生对图案的美感,又可以从图案的构成方法去认识图案的结构. 特别是对“基本图形”的不同选择,运用不同的变换方法可获得某些相同的特殊图形. 由于“基本图形”的相对性,事物运动变化的多样性,这有利于培养学生的辩证唯物主义的认识观. 课本通过上述指导思想和具体操作方法,结合课本的配套练习,能有效地培养学生的识图和构图的能力.
3 为证明平面几何习题提供重要的动态分析方法
解题的本质是把题目的条件信息和结论信息建立起科学的联系[2]. 解题的表述就是阐述其科学联系的建立过程的具体理由. 在这种意义上说,解(证)几何题就需要不断地变换前后步骤的“形式”或“思想”. 解数学题的灵魂就是“合理变化”. 合理的变化中常会拓展出解题所需要的一片新天地,缺失合理变化时常会在呆滞中一筹莫展. 既然解证几何题需要不断地合理变化,那么解(证)几何题的分析就必须适时运用运动变化的观点和方法.
因为绝大多数“静态”的数学题都是在某种动态环境下,静止于某种特殊情况时的特殊状态,它就像“运动物体”在某一时刻的所拍下的“照片”,所以要把数学题赋予为“灵性之物”,要研究它由谁以怎样的运动方式产生,静止于何时之状. 对于全等图形来说,就需要观察分析图形的平移、旋转和翻折运动,明确数学题中的图形是通过怎样的运动形成. 让相关的图形“动起来”之后,就能突显它们之间特殊的位置关系和大小关系,就容易从中分析捕捉到重要的解题信息和发现解题方法. 例如:

图1
题1 已知:如图1,△ABC,∠ACB=90°,CD⊥AB于D,AE是△ABC的角平分线,AE交BC于E,AE交CD于F, EG⊥AB于G,
求证:CF = EG.
(1)用动态分析方法研究题1构成机理,发现题1的解题信息
①从相关图形旋转考虑
如图1,给定Rt△ABC,斜边AB上的高CD就确定了. 把射线AE绕点A沿逆时针方向从AB旋转到AC时,点E由点B运动到点C,同时点F由点D运动到点C,点G由点B运动到点D,于是CE由BC退缩为点C,CF由CD退缩为点C, 线段EG在平移中由点B逐步“长高”到CD. 因为在此运动中,CE 、CF与EG都是同时开始、同时结束的连续变化的线段,且CE与CF都由长变为短,EG由短变长,它们的长度“最小值”都是零,所以必有CE = EG和CF = EG.
当CE = EG时,又AE是公共斜边,所以Rt△AEC≌Rt△AEG(HL定理),所以∠4=∠5. 此时,AE正好是△ABC的角平分线.
反过来,只要在动态的变化中把“AE是△ABC的角平分线”的特殊情况“静止”下来,那么题1的条件就全有了,并且依据角平分线性质定理,立即可得∠4=∠5,CE = EG(角平分线上的点到角的两边距离相等). 在Rt△AEC和Rt△AFD中,因为∠1与∠4互余,∠3与∠5互余,又∠4=∠5,所以∠1=∠3. 因为∠2与∠3是对顶角,所以∠2=∠3. 所以∠1=∠2,所以CE =CF. 又CE = EG,所以CF = EG.
这种利用某图形旋转建构动态分析,既能说明题1的存在性和这种构造理由,又能探究出题1的一种证明方法,且发现了与结论相关的线段CE是证明本题之关键.
②从相关图形的轴对称考虑
对题1,给定Rt△ABC,斜边AB上的高CD就确定了. 因为AE是Rt△ABC的角平分线,所以∠4=∠5. 又Rt△ABC的直角边AC必小于它的斜边AB,所以把Rt△AEC沿AE翻折180°,所以AC必然落在AB上,从而得到Rt△ABC关于直线AE对称的△AEG. 因为∠ACB=90°,所以EG必垂直AB于G. 这就有了题1的全部条件. 也找到了从“证明三角形全等”入手的解题方法. 易证∠4=∠5,∠ACB=∠AGE=Rt∠,又AE是公共边, 所以Rt△AEC≌Rt△AEG(AAS),所以CE = EG,∠1=∠AEG. 又因为EG⊥AB,CD⊥AB,所以CD∥EG,所以∠2=∠AEG. 又∠1=∠AEG,所以∠1=∠2,所以CE =CF. 又CE = EG,所以CF = EG.
这种利用某图形翻折建构动态分析,既能从新的角度说明题1的存在性和构造理由,又能探究出题1的新的证明方法. 此外,还可以从中收获其他解题信息,例如:由于两个图形关于直线对称,对称点的连线被对称轴垂直平分. 所以AE垂直平分CG,所以CF =FG,CE = EG(线段垂直平分线上的点,到线段两个端点等远). 等等.
③从相关图形的平移考虑
如图1,给定Rt△ABC,斜边AB上的高CD就确定了. 让直线EG从CD开始向右平移到经过点B,让直线FG从BC开始向下平移到经过点D,对应的线段EG和FG都分别由长变短,它们的长度“最小值”都是零,所以必有FG = EG情况存在. 而夹在两平行线之间的平行线段相等,所以有CF = EG. 在此特殊情况下,必有CE = EG,由于有∠ACB=Rt∠,EG⊥AB于G的给定条件,所以AE也正好是△ABC的角平分线. 由于相关的部分图形的对称性,此时点F就在AE上. 这就说明了题1成立,找到了证明CE = EG是证明题1的关键.
(2)用动态分析方法研究题1的关联题,探究变式解题教学方法.
在题1的条件下,由上述分析和推理已知CF = CE = EG,又CF与 EG都垂直于AB,所以四边形CFGE是菱形. 于是把题1改造成题2
题2 已知:如图2,△ABC中,∠ACB=90°,CD⊥AB于D,AE是△ABC的角平分线,AE交CD于F,AE交BC于E,EG⊥AB于G,
求证:四边形CFGE是菱形.

图2
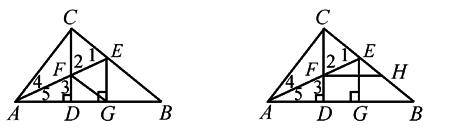
图3
在题1的条件下,由上述分析和推理已知CF = EG,又CF与 EG都垂直于AB,若再作FH∥AB交BC于H,于是可推出Rt△CFH≌Rt△EGB(AAS),从而有CH=EB. 所以有CH-EH=EB-EH,即CE=BH. 于是把题1改造成题3
题3 已知:如图3,△ABC中,∠ACB=90°,CD⊥AB于D,AE是△ABC的角平分线,AE交CD于F,AE交BC于E,EG⊥AB于G,FH∥AB交BC于H,
求证:CE=BH. (或求证CF=BH)
综上所述,在解题教学中探究关联题的变式联系,也常需要对数学题及它们的解答进行动态分析探究.
物质的世界里,事物的运动变化造就了事物间的联系形式具有多样性. 许多事物的“隐蔽”联系形式常需用动态分析方法去探究发现. 从哲学意义上说,“解题”就是不断探究发现“未知世界规律”的过程,因此解题教学要重视关联题的研究,加强变式解题示范,充分发挥三种变换的作用,适时运用动态分析的研究方法去解题.
参考文献
[1] 马复主编.义务教育课程标准实验教科书《数学》 (七年级下册 八年级上册 )[M].北京师范大学出版社,2005.
[2] 邱卫平.建构“选择·探究·发展”的解题教学模式@提高中学数学的解题教学效率[J].数学教育研究,2006,(1).
作者简介 邱卫平 (1953-),男,湖南常德人,中学数学高级教师,特级教师,长期从事中学数学教学与研究,曾参与深圳市中考数学考试说明的编写与修改,多次担任深圳市中考数学命题组长,先后多次担任过中考阅卷组长和阅卷质量检查组长.

