关于硬杆对物体弹力方向的讨论
关亚男


受力分析题中,轻绳、轻弹簧、轻质硬杆对物体的弹力方向是有所区别的.轻绳的弹力一定沿绳并指向其收缩的方向,轻弹簧的弹力一定沿着弹簧的中心轴线指向其恢复形变的方向,而轻质硬竿的弹力方向不一定在杆所在的直线上,具体剖析如下.
首先,轻质硬杆的弹力方向是否与硬杆共线,取决于硬杆与物体的接触点可动与否,可动的我们不妨称其为“活”杆,不可动的我们不妨称其为“死”杆.即“活”杆弹力方向与硬杆共线,“死”杆弹力方向与硬杆异线.
一、硬杆弹力方向与硬杆共线
当硬杆弹力方向与硬杆共线时,和弹簧相似,有向里的拉力和向外的支持力两种可能,这也是硬杆与绳的最大区别之所在,
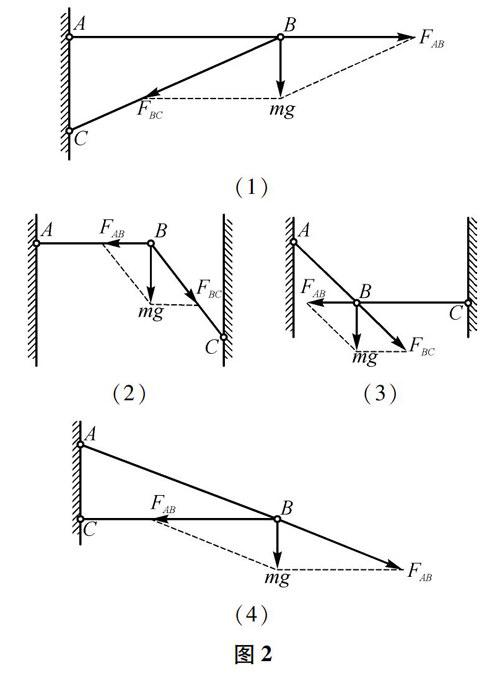
例1 在如图1所示的四张图中,AB、BC均为轻质杆,各图中杆的A、C端都通过铰链与墙连接,两杆都在B处由铰链相连接.下列说法正确的是
()
A.图中的AB杆可以用与之等长的轻绳代替的有(1)、(2)
B.图中的AB杆可以用与之等长的轻绳代替的有(1)、(3)
C.图中的BC杆可以用与之等长的轻绳代替的有(2)、(3)
D.图中的BC杆可以用与之等长的轻绳代替的有(2)、(4)
解析 本题中,B处是铰链,对轻质硬杆AB、BC的力一定与其共线.而AB与BC之所以受到力的作用,是悬挂重物的结果,不妨将重物的重力分解.如果分力沿杆指向外侧,即可以用轻绳代替;如果分力沿杆指向内侧,则是不可以用轻绳代替的.其重力分解图如下,显然正确答案是B.
答案B
二、硬杆弹力方向与硬杆异线
当硬杆弹力方向与硬杆异线时,其大小和方向往往要通过其他条件,应用牛顿第二定律来判断,是绝对被动的力.
例2 如图3所示,小车上固定着硬杆,杆的端点固定着一个质量为m的小球.当小车有水平向右的加速度且逐渐增大时,杆对小球的作用力的变化(用F1至F4变化表示)可能是下图中的( OO'沿杆方向) ()
解析 由题意知小球受重力和硬杆给的弹力两个外力,此中小球与硬杆间是“死”的,其弹力方向不一定沿杆所在直线.不过,小球的加速度与小车的加速度是相同的,而小车的加速度由题意知水平向右,可知小球所受的合力一定水平向右.这样,对小球来讲,已知合力的方向和其中一个竖直向下的分力,另一分力就不难画出.究其实质,可以理解为硬杆对小球弹力的竖直分力与小球重力平衡,另一水平分力提供加速度,明显图C是正确的.
例3 如图5所示,滑轮本身的质量忽略不计,滑轮轴安在一根轻木杆B上,一根轻绳AC绕过滑轮,A端固定在墙上,且绳保持水平,C端下面挂一个重物,BO与竖直方向夹角θ=45°,系统保持平衡.若保持滑轮的位置不变,改变θ的大小,则滑轮受到木杆的弹力大小变化情况是 ()
A.只有角θ变小,弹力才变大
B.只有角θ变大,弹力才变大
C.不论角θ变大或变小,弹力都变大
D.不论角θ变大或变小,弹力都不变
解析 本题以定滑轮为研究对象,受到A、C两股绳的拉力和B杆的支持力,B杆一旦固定,对滑轮的力的方向不一定沿杆所在直线.由于系统保持平衡,C股绳的拉力大小等于重物的重力,而A股绳拉力的大小等于C股绳拉力的大小,也等于重物的重力,则B杆的拉力与两股绳拉力的合力等值反向,与杆B和竖直的夹角大小无关,故正确选项为D.
例4 如图6甲所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10 kg的物体,∠ACB =30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EC与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量也为10 kg的物体.g取10 m/S2,求
(1)绳AC段的张力FAC与细绳EG的张力FEC之比;
(2)轻杆BC对C端的支持力FBC;
(3)轻杆HC对G端的支持力FHC.
解析 由题意可知图甲中的BC杆是“死”的,图乙中的HC杆是“活”的,这就对比说明了图甲中BC杆的力不一定沿杆所在直线,而图乙中HG杆的力一定沿杆所在直线,而图的受力分析如图所示.可见,图甲中AC绳的力FAC等于重物重力M1g =100 N,BC杆的支持力与CA绳、CD绳的拉力的合力构成等边三角形,其大小也为100 N,方向在∠ACD的反向延长线上.图乙中的HC杆的支持力与EG、GF绳的拉力的合力构成30°的直角三角形,三者的大小之比为√3:1:2.
例5 如图7所示,AC是上端带定滑轮的固定竖直杆,质量不计的轻杆AB一端通过铰链固定在A点,另一端B悬挂一重为G的物体,且B端系有一根轻绳并绕过定滑轮C,用力F拉绳,开始时∠BAC>90°,现使∠BAC缓慢变小,直到杆AB接近竖直杆AC.此过程中(不计摩擦) ()
A.拉力F逐渐减小
B.拉力F大小不变
C.轻杆B端所受轻绳的作用力大小不变
D.轻杆B端所受轻绳的作用力先减小后增大
解析 此题A端是“活”的,AB杆给的力只能沿杆.以结点B为研究对象,受到两股绳及轻杆所给外力平衡,如图8所示其等效矢量三角形与△ABC相似,
得出正确选项A、C.
三、硬杆弹力方向与硬杆垂直
套在硬桿上的物块沿着硬杆滑动时,硬杆对物块的弹力方向一定垂直于硬杆的.
例6 如图9所示,一条细绳跨过定滑轮连接物体4、B,A悬挂起来,B穿在一根竖直杆上,两物体均保持静止,不计绳与滑轮、B与竖直杆间的摩擦.已知绳与竖直杆间的夹角为θ,则物体A、B的质量之比mA:mB等于
()
A. cos θ: 1
B. 1: cos θ
C. tan θ: 1
D. 1: sin θ
解析 题中系统静止,以物体B为研究对象,受到地球给的沿竖直杆向下的重力、绳斜向左上的拉力、垂直竖直杆水平向右的弹力,竖直向下的重力与水平向有的弹力的合力恰与绳的拉力平衡,如图10所示,二绳的拉力大小又与重物A的重力相等,则
F:mBg =mAg: mBg
mA:mB=1:cos θ,
选项B正确.
例7 如图11所示,倾斜固定直杆与水平方向成60°角,直杆上套有一个圆环,圆环通过一根细线与一只小球相连接当圆环沿直杆下滑时,小球与圆环保持相对静止,细线伸直,且与竖直方向成30°角.下列说法中正确的是 ()
A.圆环不一定加速下滑
B.圆环可能匀速下滑
C.圆环与杆之间一定没有摩擦
D.圆环与杆之间一定存在摩擦
解析 由图可知,套在斜杆上的小环与细绳下的小球相对静止,二者加速度相同,方向沿斜杆向下.对小球受力分析可知,加速度大小为gsin 30°.对小环受力分析,有竖直向下的重力、垂直斜杆向上的弹力及可能存在的沿斜杆方向的静摩擦力.由于小环重力沿斜杆向下的分力产生的加速度为gsin60°大于合加速度gsin 30°,可知存在着沿斜杆向上的静摩擦力.只有选项D正确.



受力分析题中,轻绳、轻弹簧、轻质硬杆对物体的弹力方向是有所区别的.轻绳的弹力一定沿绳并指向其收缩的方向,轻弹簧的弹力一定沿着弹簧的中心轴线指向其恢复形变的方向,而轻质硬竿的弹力方向不一定在杆所在的直线上,具体剖析如下.
首先,轻质硬杆的弹力方向是否与硬杆共线,取决于硬杆与物体的接触点可动与否,可动的我们不妨称其为“活”杆,不可动的我们不妨称其为“死”杆.即“活”杆弹力方向与硬杆共线,“死”杆弹力方向与硬杆异线.
一、硬杆弹力方向与硬杆共线
当硬杆弹力方向与硬杆共线时,和弹簧相似,有向里的拉力和向外的支持力两种可能,这也是硬杆与绳的最大区别之所在,
例1 在如图1所示的四张图中,AB、BC均为轻质杆,各图中杆的A、C端都通过铰链与墙连接,两杆都在B处由铰链相连接.下列说法正确的是
()
A.图中的AB杆可以用与之等长的轻绳代替的有(1)、(2)
B.图中的AB杆可以用与之等长的轻绳代替的有(1)、(3)
C.图中的BC杆可以用与之等长的轻绳代替的有(2)、(3)
D.图中的BC杆可以用与之等长的轻绳代替的有(2)、(4)
解析 本题中,B处是铰链,对轻质硬杆AB、BC的力一定与其共线.而AB与BC之所以受到力的作用,是悬挂重物的结果,不妨将重物的重力分解.如果分力沿杆指向外侧,即可以用轻绳代替;如果分力沿杆指向内侧,则是不可以用轻绳代替的.其重力分解图如下,显然正确答案是B.
答案B
二、硬杆弹力方向与硬杆异线
当硬杆弹力方向与硬杆异线时,其大小和方向往往要通过其他条件,应用牛顿第二定律来判断,是绝对被动的力.
例2 如图3所示,小车上固定着硬杆,杆的端点固定着一个质量为m的小球.当小车有水平向右的加速度且逐渐增大时,杆对小球的作用力的变化(用F1至F4变化表示)可能是下图中的( OO'沿杆方向) ()
解析 由题意知小球受重力和硬杆给的弹力两个外力,此中小球与硬杆间是“死”的,其弹力方向不一定沿杆所在直线.不过,小球的加速度与小车的加速度是相同的,而小车的加速度由题意知水平向右,可知小球所受的合力一定水平向右.这样,对小球来讲,已知合力的方向和其中一个竖直向下的分力,另一分力就不难画出.究其实质,可以理解为硬杆对小球弹力的竖直分力与小球重力平衡,另一水平分力提供加速度,明显图C是正确的.
例3 如图5所示,滑轮本身的质量忽略不计,滑轮轴安在一根轻木杆B上,一根轻绳AC绕过滑轮,A端固定在墙上,且绳保持水平,C端下面挂一个重物,BO与竖直方向夹角θ=45°,系统保持平衡.若保持滑轮的位置不变,改变θ的大小,则滑轮受到木杆的弹力大小变化情况是 ()
A.只有角θ变小,弹力才变大
B.只有角θ变大,弹力才变大
C.不论角θ变大或变小,弹力都变大
D.不论角θ变大或变小,弹力都不变
解析 本题以定滑轮为研究对象,受到A、C两股绳的拉力和B杆的支持力,B杆一旦固定,对滑轮的力的方向不一定沿杆所在直线.由于系统保持平衡,C股绳的拉力大小等于重物的重力,而A股绳拉力的大小等于C股绳拉力的大小,也等于重物的重力,则B杆的拉力与两股绳拉力的合力等值反向,与杆B和竖直的夹角大小无关,故正确选项为D.
例4 如图6甲所示,轻绳AD跨过固定在水平横梁BC右端的定滑轮挂住一个质量为10 kg的物体,∠ACB =30°;图乙中轻杆HG一端用铰链固定在竖直墙上,另一端G通过细绳EG拉住,EC与水平方向也成30°,轻杆的G点用细绳GF拉住一个质量也为10 kg的物体.g取10 m/S2,求
(1)绳AC段的张力FAC与细绳EG的张力FEC之比;
(2)轻杆BC对C端的支持力FBC;
(3)轻杆HC对G端的支持力FHC.
解析 由题意可知图甲中的BC杆是“死”的,图乙中的HC杆是“活”的,这就对比说明了图甲中BC杆的力不一定沿杆所在直线,而图乙中HG杆的力一定沿杆所在直线,而图的受力分析如图所示.可见,图甲中AC绳的力FAC等于重物重力M1g =100 N,BC杆的支持力与CA绳、CD绳的拉力的合力构成等边三角形,其大小也为100 N,方向在∠ACD的反向延长线上.图乙中的HC杆的支持力与EG、GF绳的拉力的合力构成30°的直角三角形,三者的大小之比为√3:1:2.
例5 如图7所示,AC是上端带定滑轮的固定竖直杆,质量不计的轻杆AB一端通过铰链固定在A点,另一端B悬挂一重为G的物体,且B端系有一根轻绳并绕过定滑轮C,用力F拉绳,开始时∠BAC>90°,现使∠BAC缓慢变小,直到杆AB接近竖直杆AC.此过程中(不计摩擦) ()
A.拉力F逐渐减小
B.拉力F大小不变
C.轻杆B端所受轻绳的作用力大小不变
D.轻杆B端所受轻绳的作用力先减小后增大
解析 此题A端是“活”的,AB杆给的力只能沿杆.以结点B为研究对象,受到两股绳及轻杆所给外力平衡,如图8所示其等效矢量三角形与△ABC相似,
得出正确选项A、C.
三、硬杆弹力方向与硬杆垂直
套在硬桿上的物块沿着硬杆滑动时,硬杆对物块的弹力方向一定垂直于硬杆的.
例6 如图9所示,一条细绳跨过定滑轮连接物体4、B,A悬挂起来,B穿在一根竖直杆上,两物体均保持静止,不计绳与滑轮、B与竖直杆间的摩擦.已知绳与竖直杆间的夹角为θ,则物体A、B的质量之比mA:mB等于
()
A. cos θ: 1
B. 1: cos θ
C. tan θ: 1
D. 1: sin θ
解析 题中系统静止,以物体B为研究对象,受到地球给的沿竖直杆向下的重力、绳斜向左上的拉力、垂直竖直杆水平向右的弹力,竖直向下的重力与水平向有的弹力的合力恰与绳的拉力平衡,如图10所示,二绳的拉力大小又与重物A的重力相等,则
F:mBg =mAg: mBg
mA:mB=1:cos θ,
选项B正确.
例7 如图11所示,倾斜固定直杆与水平方向成60°角,直杆上套有一个圆环,圆环通过一根细线与一只小球相连接当圆环沿直杆下滑时,小球与圆环保持相对静止,细线伸直,且与竖直方向成30°角.下列说法中正确的是 ()
A.圆环不一定加速下滑
B.圆环可能匀速下滑
C.圆环与杆之间一定没有摩擦
D.圆环与杆之间一定存在摩擦
解析 由图可知,套在斜杆上的小环与细绳下的小球相对静止,二者加速度相同,方向沿斜杆向下.对小球受力分析可知,加速度大小为gsin 30°.对小环受力分析,有竖直向下的重力、垂直斜杆向上的弹力及可能存在的沿斜杆方向的静摩擦力.由于小环重力沿斜杆向下的分力产生的加速度为gsin60°大于合加速度gsin 30°,可知存在着沿斜杆向上的静摩擦力.只有选项D正确.

