众筹筑屋优化设计方案
朱长新 傅旭
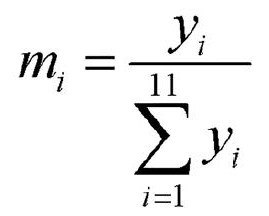
摘要:文章按照众筹筑屋方案限定的种类规划各房型的修建数量,依据大小、价格等基本信息进行统计分析,通过参筹登记网民对各种房型的满意比例调查表,计算出参加登记的人群比例,以所有人满意度和房地产公司双赢为最高目标,建立优化模型并得出设计规划方案。
关键词:众筹筑屋;优化模型;满意度;投资回报率
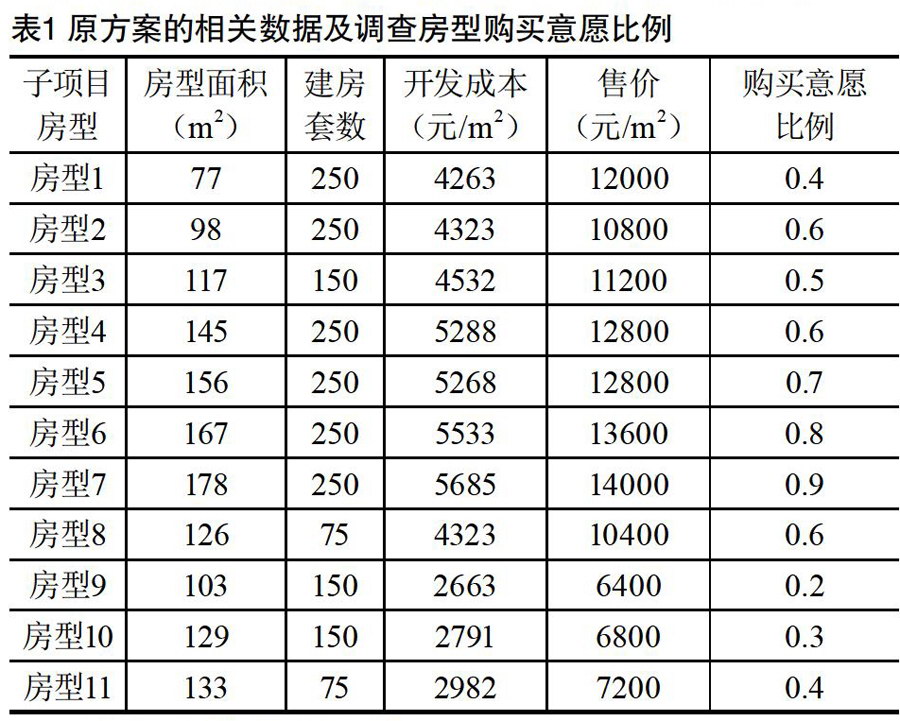
众筹筑屋是互联网时代一种新型的房地产形式。占地面积为102077.6m2的众筹筑屋项目推出后,上万户购房者登记参筹。项目规定,参筹者每户只能认购一套住房。该项目在公布建设原设计方案的基本信息后,通过对参筹者进行抽样调查,得到了参筹者对11种房型购买意愿的比例。为了尽量满足参筹者的购买意愿,需重新设计建设规划方案(见表1)。
1 对原方案进行统计分析
全面核算各项指标因素,建立成本、收益、容积率和增值税模型。引入增值率K(增值额与扣除项目金额的比率),对不同住宅类型分别建立3种增值税模型。通过Excel计算结果为:容积率F=-2.275,总收益与总成本相比占19%,房型2享受免税政策,房型9和房型10是负增值税,且房型3、8、11的收益为负数,处于亏损状态(见表2)。
2 以用户满意度设计新的方案
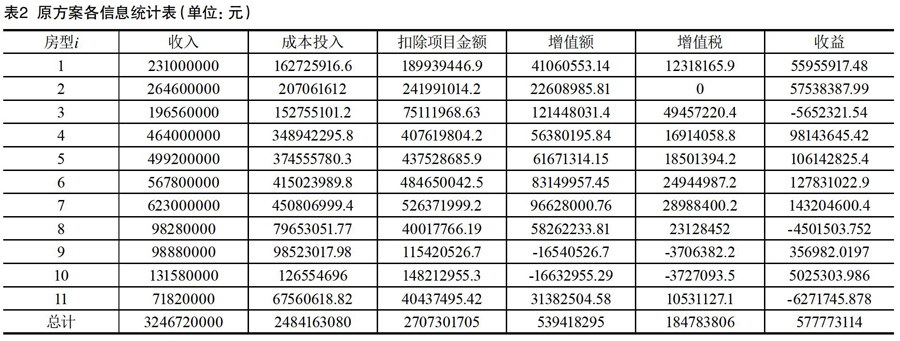
原方案没有考虑到参筹者的购买意愿,为更好地实施民主决策,对参筹者进行抽样调查,尽可能地满足参筹者的意愿来设计新的规划方案。将各种户型满意比例记为yi(i=1,…,11),显然调查是一人多选的情况,因此先对满意比例归一化处理,设mi(i=1,…,11)为归一化后第i房型的满意率,也就是第i房型的满意程度。则归一化公式为:
尽量满足参筹者的购买意愿,可看作在房型比例与满意比例相同的情况下,房型总套数最大。在容积率、各房型套数限制的条件下,寻找满意度最大的设计方案。通过建立最优化模型,并且把满意率mi代入上述最大值模型,利用Lingo软件求解可得:当房型的总套数为1920时,容积率为F=2.24<2.28,符合国家规定要求。在满意度最高的情况下,各个户型对应的套数如表3所示。
房型9、房型10和房型11的套数xi能取到限制范围的最高套数,因为这3种房型的建筑面积不纳入容积率的计算中。而此时的总收益只占17%,比原方案降低了3%,这是满意比例约束造成的,约束条件越多,房型套数受到的约束就越大,还有一个使收益降低的原因就是中房型套数1920小于原方案的房型套数2100。
在原方案中3个普通型住宅类型,房型1和房型2均能享受免税政策。房型9和房型10的增值额是负值,所以增值税时都规定为零,不参与增值税总额的核算。并可以看到,房型3,8,9,11的收益为负值,说明此4种房型是不盈利的。
3 建立最优化模型
众筹项目方案是否执行的关键在于投资回报率是否超过25%,投资回报率z是利润(最终收益)L与总投资额之比。投资额记为O,包括该项目所有的费用。这里包括取得土地支付的金额A、总开发成本B、开发费用C与转让房地产有关的税金D及增值税T共5项,计算公式为:O=A+B+C+D+T,化简得D=G+T,所以投资回报率公式为
通过投资回报率公式发现,在用户满意度最高的方案中,投资回报率Z=18.8%<25%,因此该方案不能被执行。因此需对方案做调整,在保证尽可能满足参筹者的购买意愿,可看作满意率高的房型尽可能多,优先考虑满意率高的房型。以满意度乘上房型套数最大作为目标函数,比原方案少了满意度比例约束这个约束条件。将决策变量、目标函数及约束条件用公式符号表示如下:
决策变量:各房型的套数,xi,i=1,…,11,且xi为正整数。
约束条件:国家规定最大容积率为2.28。
各房型建设最低套数与最高套数约束:nli≤xi≤nhi,i=1,…,11。
整数约束,各房型套数xi,i=1,…,11为整数。
综上,建立新方案的模型
利用Lingo软件求解,结果如下:(1)最大的满意度为246.66。(2)房型的总套数为2883。(3)容积率F=2.2799<2.28,符合国家规定要求。(4)投资回报率Z=26.02%>25%,方案3可成功执行。
对应各房型的套数如表4所示。
表中的房型9、房型10和房型11的套数xi能取到限制范围的最高套数,因为这3种房型的建筑面积不纳入容积率的计算中。
对房地产总成本投入与最终收益这两个比较分析可知,总收益只占22%,比原方案高了3%。因为此方案中房型的总套数为2883均大于原方案。而容积率F=2.2799更接近2.28,说明建筑面积更大,在盈利的情况下建筑面积越大收益也越大。使用新的房型套数,通过统计核算,各房型的成本投入、增值税及收益的核算结果如图1所示。
可以看到部分房型收益为负值,说明此类房型是不盈利的。从中也可以看出成本占的比例最大,而增值税占很小的比例,大概为收益的1/3。因此要提高收益理应尽可能地降低成本。
4 模型的评价与推广
观察各房型售价与开发价格的比值可看到,经济型、舒适型、特殊型3类房型中的代表性的房型1、房型7、房型10都在同类中比值最高,可以认为是最赚钱的。而根据满意度设计出的方案所规划的3个房型比原方案有大幅增长,房型数量大大超过了其他同类房型,故新方案对开发商来说也是更有利的,同时满足了容积率小于原方案,更加符合国家政策,可以实现国家、开发商、购房者三方共赢,进一步验证了文中所建模型的合理性。

