一种基于多维聚类预处理的云计算任务调度算法

2024.01.30

邵雯娟

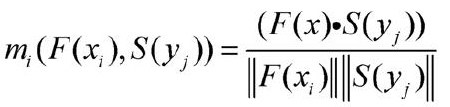
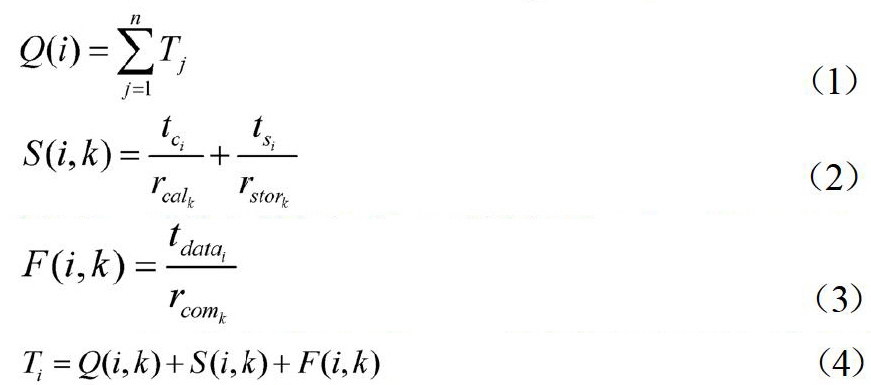
摘要：文章主要介绍了一种基于多维聚类预处理的云计算任务调度算法，根据预先分类好的资源特征向量进行分类依据，将云计算资源与特征向量间的相似度距离作为测度函数，将资源划分到预先定义好的类别中。本调度算法对资源进行分类预处理，能有效缩小任务对于资源搜索的范围，从而提高任务调度的速度。关键词：特征向量；相似度测度；任务调度

1 研究背景

云计算主要采用虚拟化技术将数据中心的物理资源虚拟化为资源节点后，进行统一管理和对外服务。用户享受的服务质量水平将会和所需支付的费用成正比。正是由于用户的不同需求，云任务调度器需要为用户任务选择合适的资源，最大限度地满足用户对于服务质量的需求，提高资源利用率，维持资源负载均衡。因此，研究云环境下的任务调度算法意义重大。

2 聚类分析法原理

聚类分析是根据样本自身的属性，用数学方法按照某种相似性或差异性指标，定量地确定样本之间的亲疏关系，并按这种亲疏关系程度对样本进行聚类。通常是用样本间的相似系数来描述其亲疏程度。有了相似系数就可定量地对样本进行分组，根据分类函数将差异最小的归为一组，组与组之间再按分类函数进一步归类，直到所有样本归为一类为止。

3 算法描述

本算法的目标是找到对资源集的一个划分，使资源性能相近或相似的节点聚在一起共同构成一个分类类别。算法的主要思想是：

（1）对训练集中的云系统资源向量事先进行手工粗分类，分为：计算型，转发型，存储型，计算出每一类的特征向量F（xi）={x1，x2，x3，…，xn）。

（2）对测试集中的云系统资源向量建立初始样本矩阵：S（yt）=（y1，y2，y3，…，yn）。

（3）用类间的相似系数来描述其亲疏程度，计算每个资源向量与各个大类的特征向量间的相似性测度函数。

Mj=（F（x1），S（yj））=（m1，m2，m3）

相关性系数定义为向量的单位化内积：

根据相似性测度函数Mj=（F（x1），S（yj））的值，根据模式分类的原则：

C（z）=ArgMiaxMj（F（x1），S（yj））

（4）比较和Si最相似的类，从而确定该资源向量的分类，将该资源和大类归并为一个类别。

（5）重复执行上述操作，直到资源池中所有资源向量都只属于同一个分类类别为止，即所有资源节点都有明确的分类类别。

（6）在每个大类中，将资源按照综合性能进行降序排序，性能较好的资源将优先被调度。

（7）对资源进行分类预处理后，在已有的分类类别中选择性能最优的资源，最大限度地体现了任务调度的公平性。

4 算法性能分析

在任务调度系统中，用户提交任务的最终完成时间取决于该任务集中所有任务的完成时间，也就是任务完成时时间最大的任务。

任务i预期完成时间L主要由队列等候时间、处理和存储时间、转发延迟时间组成。

队列等候时间可用公式（1）计算得出：（1）

Q（i）表示任务Ti在分类类别中在任务队列中等待调度的时间，n表示任务i前面的任务数，Tj表示第j个任务的预期完成时间。

处理和存储时间可用公式（2）计算得出：（2）

S（i，k）表示任务Ti使用资源k时，所需的计算执行时间，tci表示任务计算量，rcalk表示资源K的计算能力，tsi表示所需存储的任务量，rstork表示资源K的存储能力。

转发延迟时间可由公式（3）计算得出：（3）

F（i，k）表示任务i使用K源后，转发任务结果所需的传输时间，tdatai指任务输出数据量，rcomk表示资源K的通信带宽能力。

因此，任务预期完成时间可以表示为：

Ti=Q（i，k）+S（i，k）+F（i，k）（4）

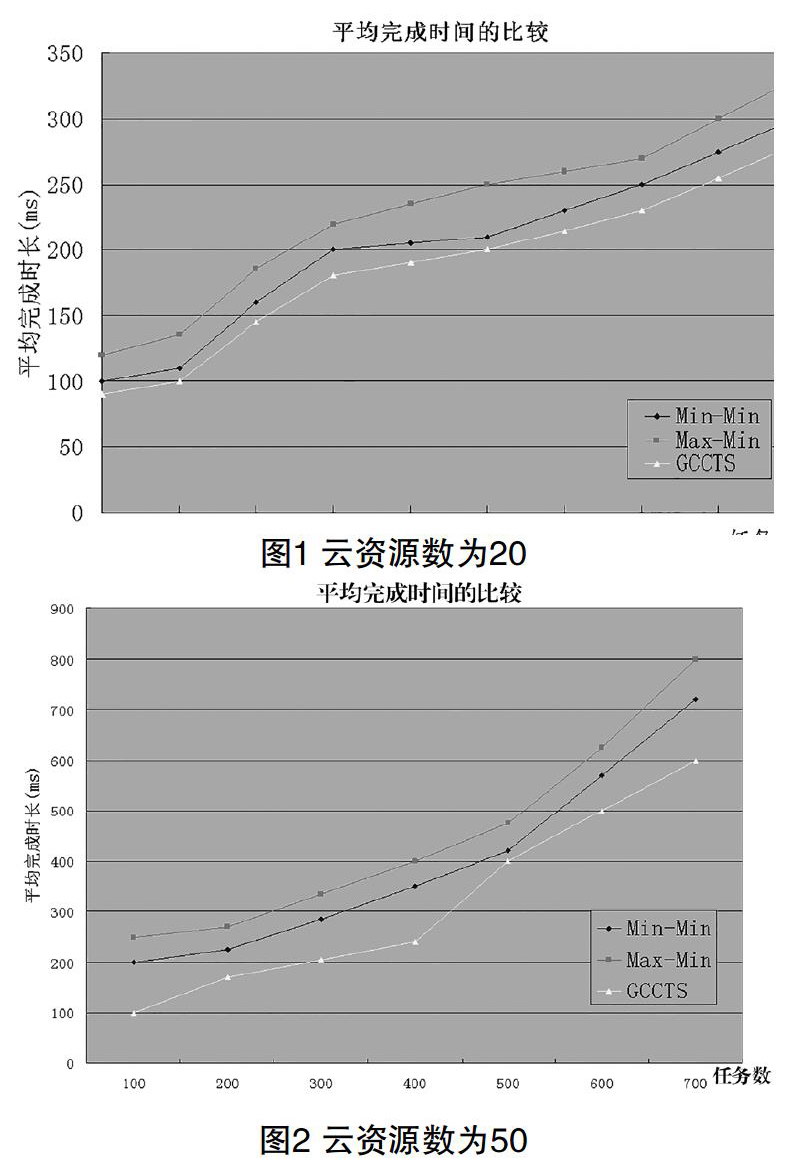
使用CloudSim仿真平台，将本调度算法（以下简称GCCTS）与Min-Min和Max-Min算法进行模拟实验调度，数据取自模拟20次取得的平均值。从调度策略的平均完成时间对3种算法进行性能比较。图1所示为资源数为20时，3种算法任务平均完成时间的比较图。图2所示为资源数为50时，3种算法任务平均完成时的比较图。

由以上分析可以看出，Min-Min算法由于每次优先选择任务完成时间最小的任务执行，因而任务最终完成时间小于Max-Min算法，但次于GCCTS算法。

5 结语

文章主要介绍一种基于多维聚类预处理的云计算任务调度算法。首先介绍了聚类分析方法，论述分类方法的具体实现步骤，利用该方法将资源划分到预先定义好的分类类别中。然后详细介绍算法的主要思想、伪代码实现，并经过对模拟环境下的实验数据分析，本调度算法对资源进行分类预处理，能有效缩小任务对于资源搜索的范围，从而提高任务调度的速度。

该调度策略仍然存在很多可改进的地方：

（1）在聚类分割时，可进一步考虑总体的资源统计特性，考虑采用马哈拉诺比距离，代替相似度度量值。

（2）云环境下的资源节点具有动态变化性，需考虑基于随机优化的动态资源分类。

（3）本文将资源划分为计算型，转发型以及存储型3个维度，可结合实际用户需求，提出多维Qos优化的云任务调度优化算法。