在数学命题探究中提升数学思维

    徐飞

    

    

    

    [摘? 要] 数学命题是数学知识体系的重要构成，在初中数学教材中涉及很多的数学命题. 对于数学命题的教学，要走出传统“抛售”式教学的误区，要引导学生经历“数学猜想——操作验证——数学证明”的过程，以此促进学生在探究数学命题的过程中达到提升数学思维能力的目标. 基于此背景，文章对“四边形內角和”一课的教学进行了探究，希望能够为广大教师提供一定的借鉴.

    [关键词] 数学命题;探究学习;数学思维;四边形内角和

    在初中数学教材中，涉及很多的数学命题，这一些数学命题是学生进行数学证明、数学解题的重要依据之一. 很多教师在教学中会直接把数学命题抛给学生进行记忆，导致学生就不能够理解数学命题的本质，从而造成了数学命题学习的被动化与肤浅化. 数学命题是一种数学判断，在数学命题教学中，教师要善于引导学生经历对数学命题的探究过程，这样，就能够有效地促进学生数学思维能力的提升. 以下结合“四边形内角和”一课的教学进行论述.

    ■ 激活原有认知，引导类比迁移

    数学知识之间是存在紧密联系的，在初中数学教学中，教师要激活学生原有的认知经验，以此引导学生进行类比迁移，这样，就能够有效地为培养他们的数学思维奠定基础.

    初中生在学习四边形之前，已经学过三角形的相关知识，本课教学的第一个环节是让学生对四边形的定义及特征进行学习. 因此在教学中，笔者先利用多媒体给学生出示交通警示牌（三角形）、广告牌（四边形）、螺丝帽（六边形）.

    师：从这一些物体的表面能够抽象出什么几何图形？

    生：从这一些物体的表面能够分别抽象出三角形、四边形还有六边形.

    师：在数学上是如何定义三角形的？

    生1：三角形就是三条线段连接而成的图形.

    生2（补充）：三条线段首尾顺次连接，这种图形称之为三角形.

    生3（再补充）：由不相同直线上的三条线段首尾顺次连接所形成的图形称之为三角形.

    师：你能够根据三角形的定义，通过类比的方式对四边形进行定义吗？

    生3：不在同一条直线上的四条线段首尾顺次连接所形成的图形叫四边形.

    师（大屏幕出示一个四边形ABCD）：那么四边形有几条边、几个角、几个顶点呢？

    生4：四边形有四条边、四个角以及四个顶点.

    在这一教学片段中，教师先引导学生根据实物抽象出三角形、四边形、六边形这三个几何图形，然后引导学生对三角形的定义进行回顾，并在此基础上让学生通过类比对四边形进行定义. 这样的设计符合学生的认知规律，可以让学生在原有的认知经验上把握四边形的定义及基本特征，同时，为学生自主探究四边形的内角和奠定基础.

    ■ 基于动手操作，初步感知命题

    初中生在学习数学知识的过程中，是遵循“形象感知——抽象提升”这一规律的，动手操作是他们对数学知识进行形象感知的重要途径. 因此，在数学命题的教学中，教师要善于引导学生开展动手操作活动，让学生在动手操作的过程中对数学命题进行初步感知.

    师：请大家在本子上画出一个四边形. （学生画图）

    师：你觉得在你画好的四边形中，四个内角一共是多少度？

    生5：我觉得是360°.

    生6：我觉得一个四边形可以分成两个三角形，所以四个内角的和应该是360°.

    师：你是否可以验证这一结论呢？（学生思考并进行操作验证）

    生7：我是把自己画的四边形的四个内角剪下，然后进行拼接，在拼接的过程中保证四个角的顶点和边重合，最后拼成了一个周角，说明四边形的内角和是360°.

    生8：我是把画的四边形的四个内角的度数用量角器量出来，然后加起来也是360°.

    师：同学们，你们真厉害，通过刚才的学习发现了一个数学命题：四边形的内角和等于360°. （板书）

    在这一环节中，教师引导学生进行动手操作能使其对四边形有更加直观的认知，随后猜想四边形内角和是360°. 然后，再引导学生对这一猜想通过拼一拼、量一量的操作进行验证，从而发现了“四边形的内角和等于360°”这一命题.

    ■ 基于原有命题，引导证明命题

    在初中数学教学中，培养学生的高阶数学思维是十分重要的. 数学证明是一种高阶的思维活动方式，引导学生对命题进行证明是关键环节. 在学生对“四边形的内角和等于360°”这一命题进行操作验证之后，引导学生基于“三角形的内角和是180°”进行证明. 教学中，笔者是这样对学生进行引导的：

    师：刚才你们通过操作验证了“四边形的内角和等于360°”这一命题. 那么，你们能不能结合已知的命题对这一命题进行证明呢？

    生9：我觉得可以在“三角形的内角和是180°”这一命题的基础上进行证明.

    师：你的想法真好，这样进行证明的关键点是什么？（学生讨论）

    生10：把四边形转化为三角形是关键点.

    师：那么，怎样才能把四边形转化成三角形呢？

    生11：可以通过画辅助线的方式把四边形转化成三角形.

    在证明“四边形的内角和等于360°”这一命题时，转化是重要的方法，以上教学环节中，教师通过引导让学生明白添上辅助线会使题目显得相对简单. 在这个过程中，能让学生深度体会证明思路的转化，提升学生的推理水平.

    师：接下来，大家就根据刚才的思路对这一命题进行证明.

    （学生自主证明命题. 在这一过程中，教师在学生之间巡视，为有困惑的学生提供帮助和点拨，当学生完成证明之后，教师组织学生反馈）

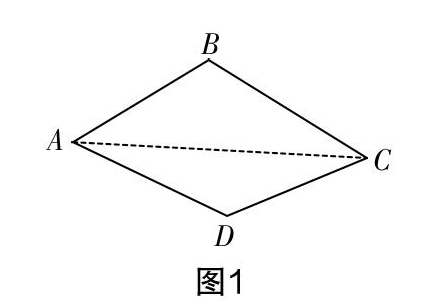
    生12：如图1，连接AC，这样就把四边形ABCD分割成了三角形ABC和三角形ACD，一个三角形的内角和为180°，两个三角形的内角和就是360°，所以四边形ABCD的内角和是360°.

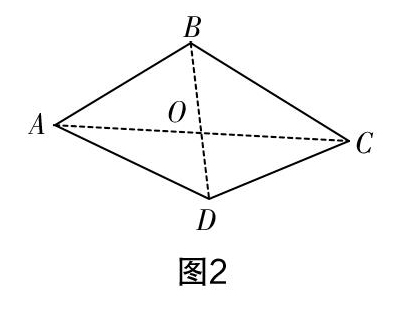
    生13：如图2，将AC，BD相连，此时四个三角形的内角之和为4×180°=720°，随后将四边形之中的周角减去，得到4×180°-360°=360°.

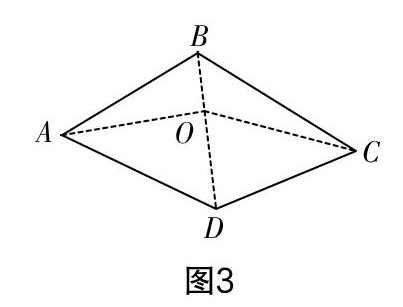
    生14：如图3，在四边形内确定一点O，连接AO，BO，CO和DO，图中四个三角形的内角和是4×180°=720°，将四边形内周角的度数减去，得到4×180°-360°=360°.

    生15：如图4，在四边形外确定一点O，连接AO，BO，CO和DO，图中△OAB，△OAD，△ODC的三个内角之和是3×180°=540°，将△OBD内角和的度数减去，得到3×180°-180°=360°.

    生16：如图5所示，将BC延长，在延长线上确定一点E，连接AE，交CD于点F，得∠BCD=∠E+∠CFE=∠E+∠AFD，此时四边形内角和等于△ABE与△ADF的内角和之和，为360°.

    以上5种方法均先让学生自主思考，然后让他们在小组内对证明的过程进行交流讨论. 这样，学生就能够在互动学习的过程中引发思维碰撞，从而开阔其证明思路，拓展他们的数学思维空间.

    总之，数学命题是初中数学知识体系的重要构成，在“核心素养”理念下，对于数学命题的教学，引导学生经历“数学猜想——操作验证——数学证明”的过程十分重要，这样，才能在这个过程中促进他们数学思维能力的有效提升.