移动终端巧融合 精准教学妙生成
景祝君 王青芳
[摘? 要] 移动终端支撑下的精准教学使教师可以有效地把握学生的学情,设计教学目标,精选教学内容与形式、精准测量学习效果.文章以“实数的运算复习”为教学尝试,整合单元数学知识、剖析思维,挖掘思想,着重体现了移动终端融合下的数学复习课的课堂教学特征.
[关键词] 移动终端;精准教学;实数;运算
移动终端支撑下的精准教学使教师可以有效把握学生学情,设计教学目标,精选教学内容与形式、精准测量学习效果. 笔者在一次课堂教学研讨活动中执教“实数的运算复习”课,为确定教学目标笔者借助ipad平板让学生完成课前预测,通过课前预测数据分析确定教学目标和教学重难点. 在备课过程中,笔者特别对移动终端融合下的初中数学复习课教学进行了探索,现将课堂生成简录、反思,整理成文,与各位同行交流.
教学目标
(1)通过前测的纠错议错,剖析错误根源,在梳理运算常见错误的过程中领悟实数运算的算理.
(2)通过中测的独立运算,理解实数运算法则和运算律,发展运算能力,提高数学运算核心素养.
(3)通過解决实际问题,感悟估算在生活中的应用,促进数学思维发展.
教学过程
1. 算24点,引出实数运算
问题:(升级版24点)请用加、减、乘、除、乘方和开方中的若干种运算(可用括号)将以下四个有理数-2,2,4,16(每个数字只能用一次)列成一个算式,使得计算结果为24. (注意:指数和底数都需从这四个数中选择 )
设计意图? 基于前测,以学生已有知识水平为起点,运用升级版的24点,引出本节课的课题“实数的运算复习”.
2. 纠错误,明晰运算法则
纠错1:计算:4÷-■×(-2)-50×■.
生1:原式=4-■=-■.
生2:原式=4×2×2-■=■.
师:这两位同学的错误在哪里?
生3:第一位同学先做了乘法运算导致错误,第二位同学减法运算错误了.
师:第一位同学的错误怎么改呢?
生4:同级运算从左往右依次计算,这里应该先算除法,除法转化为乘法,再算乘法.
师:除法转化为乘法!我们要清楚除法和乘法的运算法则.
师:第二位同学的减法运算错在哪里?
生5:减法运算先转化为加法运算,16+-■,这里是异号两数相加结果是负数.
师:对!减法运算转化为加法运算. 加法运算应先确定符号,再进行绝对值运算.
纠错2:计算:-1■2+(-22)-■.
生1:原式=1■+4-4=1■.
师:这位同学的错误在哪里?
生2:乘方运算错误. 第一个的底数是带分数,转化成假分数-■,-■2=■,第二个的底数是2,不是-2.
师:说得很好!乘方运算一定要辨认底数,我们要回归乘方的意义,乘方转化成乘法,-1■2=-■2=-■×-■=■.那么-22表示什么意思呢?
生3:表示2×2的相反数,结果是-4.
师:这题里除了乘方运算还有开方运算,开方运算又是怎么算的呢?
生4:■表示16的算数平方根,因为42=16,所以16的算数平方根是4.
纠错3:计算:15÷5×(-3)-■÷■-■.
生1:原式=3×(-3)-6÷■-■ =
-9-6×■-6×■=-9-4-9=-22.
师:这位同学的错误又在哪里?
生2:除法没有分配律.他用分配律进行运算是错误的.
师:这里除法运算中不能用分配律,为什么除法没有分配律呢?
生3:除法是已知两个因数的积与其中一个因数,求另外一个因数的运算,前一个叫被除数,后一个叫除数,除数是一个整体.
师:除了分配律外,运算律还有哪些?
师生互动一起回顾运算律.
交换律:a+b=b+a,a×b=b×a.
结合律:(a+b)+c=a+(b+c),(ab)c=a(bc).
分配律:a×(b+c)=a×b+a×c.
师:因为加数与加数,因数与因数的地位相等,所以这里只有加法和乘法有交换律和结合律. 现在明确运算法则,理解了运算律后来试一试.
设计意图? 利用学生错题资源是提升学生反思能力的有效途径之一. 通过学生课前前测中的错题展示,在纠错过程中明晰减法和加法、乘法和除法、乘方和开方的运算法则,明确减法和加法、乘法和除法、乘方和开方的互逆关系,让学生既了解“怎样运算”,又能从算理的角度理解“为什么这样算”的道理.
3. 限时练,巩固运算法则
计算:
(1)(-1.25)÷■×(-23)-■÷-1■2.
(2)■+■-(-1)2018.
(3)[5+2(■-2)]-2×(■-1).
设计意图? 教师通过iPad平板推送三个题让学生独立计算. 要求每个小题限时2分钟完成. 学生逐步提交答案,教师在平板中进行批改,及时反馈学生. 学生全部完成后,教师通过平板展示班级整体答题情况,让学生复习实数运算的顺序并感悟到运算不仅要正确,而且要灵活、合理、简洁.
4. 巧估算,灵活应用运算
应用1:某公路段规定汽车的行驶速度每小时不得超过80 km. 当发生交通事故时,交通警察通常根据刹车后车轮滑过的距离来估计车辆行驶的速度,所用的公式是v=16■. 其中v表示车速(单位:km/h),d表示刹车后车轮滑过的距离(单位:m).经测定,某肇事汽车刹车后车轮滑过的距离d=20 m,请估算该肇事汽车当时是否超速.
应用2:数轴上两点A,B分别表示实数■和■-1,求A,B两点之间的距离.
变式:数轴上两点A,B分别表示实数 a和b,求A,B两点之间的距离.
课后探究:数轴上两点A,B分别表示实数■和■-1,在数轴中找出一个点C,使它到 A,B两点之间的距离相等.
设计意图? 通过“应用1”的实际情境让学生感受到实数运算的实际价值,“应用2”回归数轴,数形结合,学生由形象思维走向抽象思维,走向深度数学思考,并通过变式练习关联代数式,为从数的体系上升到从式的体系做铺垫,思想提领,学生“自得”,提升了学生数学学习素养.
5. 善小结,建构运算规律
教师:通过实数运算复习,你学到了什么知识和方法?获得了哪些活动经验?
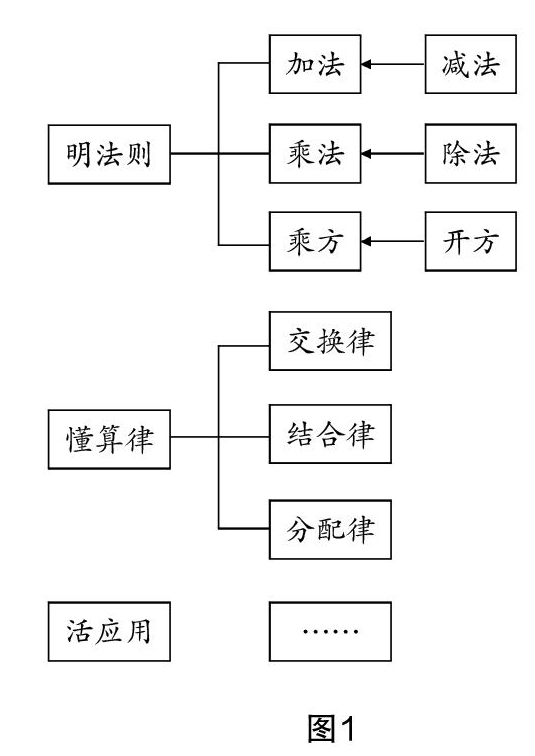
师生共同小结完成下列导图(实数运算复习):
6. 课后测,检测课堂效果
(1)估计■ 的值的范围是(?摇?摇?摇? ?)
A. 2到3之间?摇? ? ?摇B. 3到4之间
C. 4到5之间?摇?摇? ? D. 5到6之间
(2)数轴上两点A,B分别表示实数2■和2■+6,则这两个点的距离是(? ? ?摇?摇)
A. 4■+6? ? ?B. 4■
C. 6? ? ? ? ? ? ? ? ? ?摇?摇?摇 D. 4■-6
(3)计算■-■的结果是(? ? ? )
A. 2? ? ? ? ? ? ? ?B.±2
C. -2或0? ? ?D.0
(4)计算■+10÷52×-■-12018.
设计意图? 通过iPad平板推送题目给每一位学生,检测学生学习效果,这是测试后的反馈数据:从数据中可以看出同学们的运算的正确性比课前有了明显进步.
教学反思
1. 三点一线——精准教学理念下移动终端融入复习课教学的课堂特征
移动终端下的数学复习课基于精准教学理念,运用课前测——课中测——课后测“三点一线”,有效借力移动终端,展现课堂新特征. (1)课前测——精准定位教学起点. 教师设计2~3道测试题,学生课前完成. 通过答题数据分析,教师能有效把握学生知识结构中存在的困惑和问题,准确定位教学目標和教学重难点. 当然,课前测试题的选题要基于课程标准和章节目标,精心挑选. 如本节复习课中笔者设置了三个涵盖实数的加、减、乘、除、乘方和开方运算的题目,测试学生是否理解算理、掌握算法. (2)课中测——高效获取学习效果. 借力移动终端,教师可以及时获得学生当堂独立练习情况,真正做到“学为中心”. 如本节“实数的运算”复习课中的“限时练,巩固运算法则”环节,教师通过iPad平板推送题目,学生独立运算后提交结果,教师及时批改,精准反馈答题情况,展示正确答案,并由答题错误的学生自己剖析错因并给予鼓励,帮助其加深对知识的理解,达到评价的精准化,助推高效学习. (3)课后测——跟进课堂学习效率. 课后测不是简单的题目堆积、累加,而是根据本节课的教学目标设置的有效作业,因此题不在多,在于“效”.
2. 择需而用——遵循精准教学理念下移动终端融入复习课教学的基本原则
《义务教育数学课程标准(2011年版)》指出:“教学中应有效地使用信息技术资源,发挥其对学习数学的积极作用,减少其对学习数学的消极作用. ”移动终端进入数学课堂,要发挥信息技术的辅助作用. 教师要根据数学教学的特点,根据学生的已有水平和教学实际,“学为中心”分阶段、有层次地精心设计iPad平板使用环节,因需而定,择需而用. 如本节“实数的运算”复习课中教师选择在课前、课中、课后三个特定的环节使用移动终端,发挥其及时反馈、数据分析的作用,其他环节仍采用师生面对面的对话交流形式,在数学思考中融入情感交流.
3. 核心素养——落实精准教学理念下移动终端融入复习课教学的数学立意
数学教学,以核心素养为纲. 教师要立足于数学知识整体结构处、数学关键能力落脚处思考学习内容从何而来、走向哪里,基于知识、能力、素养三个层面低起点、高立意设计教学. 如数学运算是在明晰运算对象的基础上,依据运算法则解决数学问题的素养,运算素养是其他素养的基础. 所以教师在复习课中不能是简单的运算题的堆砌和训练,而应从算理、算律的角度出发,让学生感悟算理、感受算法;同时,要注重通过各部分知识的关联、贯通、整合来培养学生的运算能力. 本节课教师在尾声从数的运算关联到式的运算,在无声处豁然开朗,数式是一家,类比探究,循序渐进,使学生在运算中也提升了数学思考的意识和能力.

