关于胡克定律和弹簧问题的分析
王飞

高中物理教材中弹簧模型是一个重要的模型,在中学阶段,凡涉及的弹簧都不考虑其质量,称之为“轻弹簧”,是一种常见的理想化物理模型.弹簧在弹性限度内遵从胡克定律,弹簧发生弹性形变时,弹力的大小F跟弹簧伸长(或缩短)的长度x成正比,即:F=kx,式中k叫做弹簧的劲度系数,单位是牛顿每米,符号是N/m.
关于胡克定律的理解要注意以下几点:
1.胡克定律的成立是有条件的,弹簧要发生“弹性形变”,即在弹性限度内才适用.
2.表达式中的x是弹簧的形变量,是弹簧伸长(或缩短)的长度,而不是弹簧的原长,也不是弹簧形变后的长度.
3.表达式中的劲度系数k,反映了弹簧的“软”“硬”程度,其大小与弹簧的材料、形状、长度有关.
4.由于弹簧的形变量x常以“cm”为单位,而劲度系数k又往往以“N/m”为单位,在应用公式时要注意将各物理量的单位统一.
5.胡克定律的另一种表达形式:设劲度系数为k的弹簧,在形变量为X1、x2时产生的弹力分别为F1、F2,则根据胡克定律F=kx,有,两式相减,有,即△F=k△x.上式表明:弹簧发生弹性形变时,弹力的变化△F与弹簧长度的变化△x成正比.
弹簧的弹力是一种由形变而决定大小和方向的力.当题目中出现弹簧时,要注意弹力的大小与方向时刻要与当时的形变相对应.在题目中一般应从弹簧的形变分析人手,先确定弹簧原长位置、现长位置,找出形变量x与物体空间位置变化的几何关系,分析形变所对应的弹力大小、方向,以此来分析计算物体运动状态的可能变化,
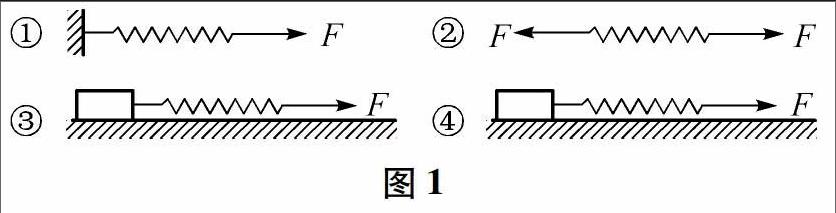
例1 如图1所示,四个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:①中弹簧的左端固定在墙上,②中弹簧的左端受大小也为F的拉力作用,③中弹簧的左端拴一小物块,物块在光滑的桌面上滑动,④中弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动.若认为弹簧的质量都为零,以依次表示四个弹簧的伸长量,则有()
解析 无论弹簧的左端情况怎样,轻弹簧的两端拉力总相等.设弹簧两端拉力分别为F、F,则F-F=ma,轻弹簧的质量为0,因此ma=0,即F=F.且此拉力等于弹簧的弹力,则根据胡克定律得到四个弹簧应该是,所以四个弹簧一样长.所以选择D选项.
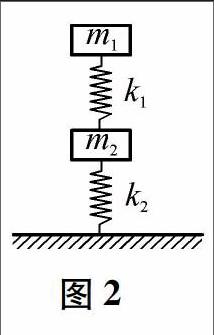
例2 如图2示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中下面木块移动的距离为()
解析 题中空间距离的变化,要通过弹簧形变量的计算求出.注意缓慢上提,说明整个系统处于一动态平衡过程,直至m1离开上面的弹簧.开始时,下面的弹簧被压缩,比原长短,而m.刚离开上面的弹簧,下面的弹簧仍被压缩,比原长短,因而m2移动的距离,所以选C.
例3 量得一只弹簧测力计3N和5N两刻线之间的距离为2.5㎝,求:
(1)这只弹簧测力计所用弹簧的劲度系数:
(2)这只弹簧测力计3N刻线与零刻线之间的距离.
解析 (1)根据
(2)由.得
点拨 F=kx是胡克定律的数学表达式,F与x的关系还可以用图象来描述,横轴为白变量x,纵轴为因变量F,其图象是一条过原点的直线,如图3所示,图象上各点的坐标(x,F)反映弹簧的一个工作状态,所以这一条直线是弹簧所有状态的集合,直线的斜率反映了弹簧的劲度系数,从图象还可以看到:F与x对应,△F与△x对应,弹簧的劲度系数可用计算,也可用计算,这样使胡克定律的应用变得更加灵活.
例4 如图4所示为一轻质弹簧的长度和弹力大小的关系图象,根据图象判断,下列结论正确的是()
A.弹簧的劲度系数为1N/m
B.弹簧的劲度系数为100N/m
C.弹簧的原长为6cm
D.弹簧伸长0.2m时,弹力的大小为4N
y解析 图线与横轴交点为弹簧原长,即原长为6cm;劲度系数为直线斜率;弹簧伸长0.2m时,弹力F=kx=100×0.2N=20N.所以选项B、C正确.
例5 如图5所示,光滑斜面倾角为θ=30°,一个重20N的物体在斜面上静止不动.轻质弹簧原长为10cm,现在的长度为6cm.
(1)求弹簧的劲度系数;
(2)若斜面粗糙,将这个物体沿斜面上移6 cru(弹簧与物体相连),物体仍静止于斜面上,求物体受到的摩擦力的大小和方向.
解析 (1)对物体受力分析,受到重力、支持力、弹簧的弹力F,则有:mgsinθ=F,此时F=kx联立代人数据得:k=250N/m
(2)物体上移,则摩擦力方向沿斜面向上,此时重力的分力加上弹簧的弹力等于物体受到沿斜面向上的摩擦力.有:Ff=mgsinθ+F此时F=kx2=5N,代人上式得Ff=15N,方向沿斜面向上.



高中物理教材中弹簧模型是一个重要的模型,在中学阶段,凡涉及的弹簧都不考虑其质量,称之为“轻弹簧”,是一种常见的理想化物理模型.弹簧在弹性限度内遵从胡克定律,弹簧发生弹性形变时,弹力的大小F跟弹簧伸长(或缩短)的长度x成正比,即:F=kx,式中k叫做弹簧的劲度系数,单位是牛顿每米,符号是N/m.
关于胡克定律的理解要注意以下几点:
1.胡克定律的成立是有条件的,弹簧要发生“弹性形变”,即在弹性限度内才适用.
2.表达式中的x是弹簧的形变量,是弹簧伸长(或缩短)的长度,而不是弹簧的原长,也不是弹簧形变后的长度.
3.表达式中的劲度系数k,反映了弹簧的“软”“硬”程度,其大小与弹簧的材料、形状、长度有关.
4.由于弹簧的形变量x常以“cm”为单位,而劲度系数k又往往以“N/m”为单位,在应用公式时要注意将各物理量的单位统一.
5.胡克定律的另一种表达形式:设劲度系数为k的弹簧,在形变量为X1、x2时产生的弹力分别为F1、F2,则根据胡克定律F=kx,有,两式相减,有,即△F=k△x.上式表明:弹簧发生弹性形变时,弹力的变化△F与弹簧长度的变化△x成正比.
弹簧的弹力是一种由形变而决定大小和方向的力.当题目中出现弹簧时,要注意弹力的大小与方向时刻要与当时的形变相对应.在题目中一般应从弹簧的形变分析人手,先确定弹簧原长位置、现长位置,找出形变量x与物体空间位置变化的几何关系,分析形变所对应的弹力大小、方向,以此来分析计算物体运动状态的可能变化,
例1 如图1所示,四个完全相同的弹簧都处于水平位置,它们的右端受到大小皆为F的拉力作用,而左端的情况各不相同:①中弹簧的左端固定在墙上,②中弹簧的左端受大小也为F的拉力作用,③中弹簧的左端拴一小物块,物块在光滑的桌面上滑动,④中弹簧的左端拴一小物块,物块在有摩擦的桌面上滑动.若认为弹簧的质量都为零,以依次表示四个弹簧的伸长量,则有()
解析 无论弹簧的左端情况怎样,轻弹簧的两端拉力总相等.设弹簧两端拉力分别为F、F,则F-F=ma,轻弹簧的质量为0,因此ma=0,即F=F.且此拉力等于弹簧的弹力,则根据胡克定律得到四个弹簧应该是,所以四个弹簧一样长.所以选择D选项.
例2 如图2示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中下面木块移动的距离为()
解析 题中空间距离的变化,要通过弹簧形变量的计算求出.注意缓慢上提,说明整个系统处于一动态平衡过程,直至m1离开上面的弹簧.开始时,下面的弹簧被压缩,比原长短,而m.刚离开上面的弹簧,下面的弹簧仍被压缩,比原长短,因而m2移动的距离,所以选C.
例3 量得一只弹簧测力计3N和5N两刻线之间的距离为2.5㎝,求:
(1)这只弹簧测力计所用弹簧的劲度系数:
(2)这只弹簧测力计3N刻线与零刻线之间的距离.
解析 (1)根据
(2)由.得
点拨 F=kx是胡克定律的数学表达式,F与x的关系还可以用图象来描述,横轴为白变量x,纵轴为因变量F,其图象是一条过原点的直线,如图3所示,图象上各点的坐标(x,F)反映弹簧的一个工作状态,所以这一条直线是弹簧所有状态的集合,直线的斜率反映了弹簧的劲度系数,从图象还可以看到:F与x对应,△F与△x对应,弹簧的劲度系数可用计算,也可用计算,这样使胡克定律的应用变得更加灵活.
例4 如图4所示为一轻质弹簧的长度和弹力大小的关系图象,根据图象判断,下列结论正确的是()
A.弹簧的劲度系数为1N/m
B.弹簧的劲度系数为100N/m
C.弹簧的原长为6cm
D.弹簧伸长0.2m时,弹力的大小为4N
y解析 图线与横轴交点为弹簧原长,即原长为6cm;劲度系数为直线斜率;弹簧伸长0.2m时,弹力F=kx=100×0.2N=20N.所以选项B、C正确.
例5 如图5所示,光滑斜面倾角为θ=30°,一个重20N的物体在斜面上静止不动.轻质弹簧原长为10cm,现在的长度为6cm.
(1)求弹簧的劲度系数;
(2)若斜面粗糙,将这个物体沿斜面上移6 cru(弹簧与物体相连),物体仍静止于斜面上,求物体受到的摩擦力的大小和方向.
解析 (1)对物体受力分析,受到重力、支持力、弹簧的弹力F,则有:mgsinθ=F,此时F=kx联立代人数据得:k=250N/m
(2)物体上移,则摩擦力方向沿斜面向上,此时重力的分力加上弹簧的弹力等于物体受到沿斜面向上的摩擦力.有:Ff=mgsinθ+F此时F=kx2=5N,代人上式得Ff=15N,方向沿斜面向上.

