运动学知识归纳
王飞


一、运动的描述
第一章是高一物理的起始章节,跟初中物理相比,高中物理内容的深度与广度都有明显的增强,学生学习物理的方法也有所不同,物理学科对学生的理解、分析、推理、综合、应用等各方面的能力要求都较高.绝不能死记硬背有关物理概念和规律,而要全面理解其内涵与外延,做到真正理解和掌握.就本章的学习,要理解质点、加速度等重要概念;要充分认识矢量这一重要概念;再次就是要认识x-t、v-t图象的意义,并能用来解决简单的问题.
在学习过程中重点要认清四个关系:
1.时刻与时间间隔的关系
时间间隔能展示运动的一个过程,在时间轴上表示一段,时刻只能显示运动的一个瞬间,在时间轴上表示一点.对一些关于时间间隔和时刻的表述,要能够正确理解.如:第2s末、2s时、第2s初等均为时刻;2s内、第2s、第2s至第3s内……均为时间间隔.
2.路程与位移的关系
位移表示位置变化,用由初位置到末位置的有向线段表示,是矢量.路程是运动轨迹的长度,是标量.只有当物体做单向直线运动时,位移的大小才等于路程.一般情况下,路程≥位移的大小.
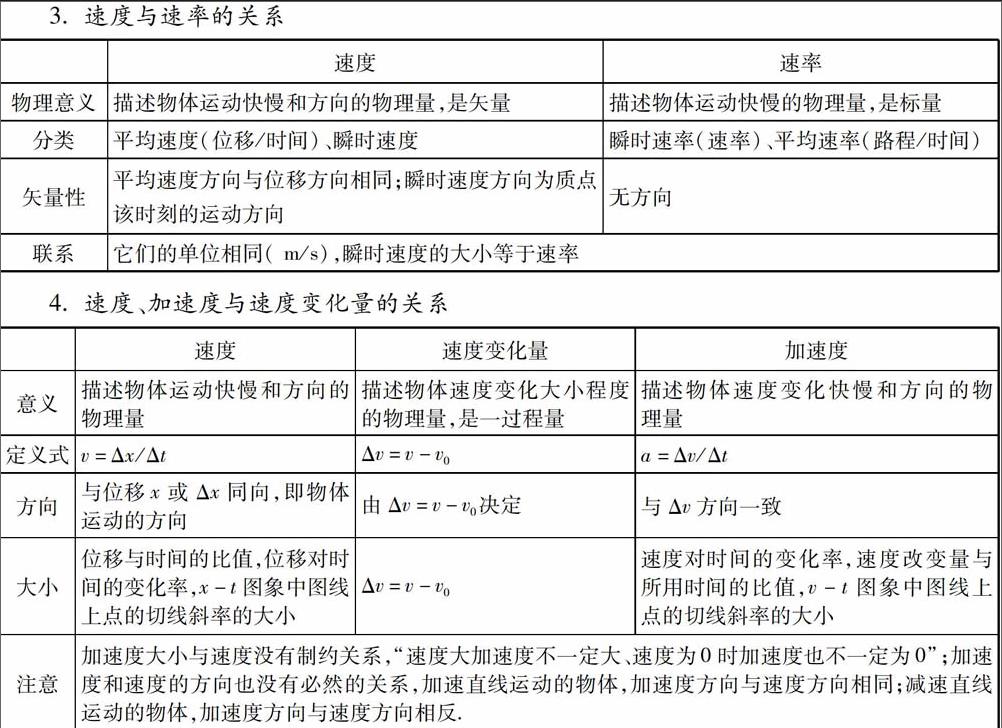
3.速度与速率的关系
二、匀变速直线运动的研究
在学习匀变速直线运动知识中一定要理解熟记公式及推论,并灵活应用解决问题.
1.公式
速度公式:v=v0+at
位移公式:
推导公式:
推论:
(1)匀变速直线运动的物体,在任两个连续相等的时间里的位移之差是个恒量,即
(2)匀变速直线运动的物体,在某段时间内的平均速度,等于该段时间的中间时刻的瞬时速度,即
.以上两推论在纸带处理中经常用到,要熟练掌握.
(3)
,某段位移的中间位置的瞬时速度公式(不等于该段位移内的平均速度).
可以证明,无论匀加速运动还是匀减速运动,都有
.
(4)初速度为零的匀加速直线运动(设T为等分时间间隔):
末速度为零的匀减速运动可以看作初速度为零的匀加速运动(逆向思维)
2.典型问题
(1)追及和相遇或避免碰撞的问题:此类问题一般有三种解法,解法一是对运动过程的分析,抓住两车间距有极值时速度应相等这一关键条件来求解;解法二是由位移关系得到一元二次方程,然后利用根的判别式来确定方程中各系数间的关系,这也是中学物理中常用的数学方法;解法三是通过巧妙地选取参照物,应用图象法和相对运动知识求解,利用相对运动的处理手段来使两车运动的关系变得简明.
关键在于掌握两个物体的位置坐标及相对速度的特殊关系.即速度相同时,两质点间距离最大或最小.基本思路:分别对两个物体研究,面出运动过程示意图,列出方程,找出时间、速度、位移的关系,建立相应的方程求解.解出结果,必要时可借助两质点的速度图象进行分析.在追赶过程中,速度相等是一个转折点:追者和被迫者速度v相等是能否追上、两者间的距离有极值、能否避免碰撞的临界条件,也就是隐含条件.
(2)相遇类问题的不同情景异同点.
①匀加速运动追及匀速运动,当二者速度相同时相距最远,
②匀速运动追及匀加速运动,当二者速度相同时追不上以后就永远追不上了.此时二者相距最近.
③匀减速直线运动追匀速运动,当二者速度相同时相距最近,此时假设追不上,以后就永远追不上了.
④匀速运动追匀减速直线运动,当二者速度相同时相距最远,
⑤匀加速直线运动追匀加速直线运动,应当以一个运动物体当参照物,找出相对速度、相对加速度、相对位移.
(2)相对运动问题:选地面或相对于地面静止的物体作为参考系,这样对物体运动的描述与我们平时的习惯相符.但在解决运动学问题时,同学们的思维不能僵化,因为同一道运动学问题,选取不同的参考系,对运动的描述以及问题解决的难易程度可能差别很大.智者化繁为简,灵活地选取合理的参考系,巧妙地解决有关的运动学问题是学生必须具备的能力.通常选取除地面外的物体(经常是运动的,且与研究对象有着一定的关联)来研究物体的运动就通俗地称为“相对运动”的解题思想.
如图1,甲球从离地面H高处 从静止开始自由下落,同时使乙球从甲球的正下方地面处做竖直上抛运动.欲使乙球上升到
处与甲球
相撞,则乙球上抛的初速度应为 多大?
如果选择地面为参考系,则甲做自由落体运动,下落高度为
,由运动学方程可得
;
乙做竖直上抛运动,若设乙球抛出的初速度为v,由运动学方程可得
两式联立解得
下面我们看看假如以自由下落的甲球为参考系,以向上为正方向,则乙球的初速度就为v相对=v0-0=v0向上,相对加速度为av相对=-g-(-g)=0,即乙将向上做匀速运动,则从抛出到两球相遇的时间为:
即等于甲自由落体的时间
可直接解得
对比发现选择相对运动系统中的物体,有时可以简化运动模型,匀速运动总比变速运动简洁吧.同学们可以自己通过实践来慢慢体会和有意识地熟练解题的方法,另外对本题同学们可以尝试选择乙物体为参考系,看看解题过程是否同样简洁.
3.匀变速直线运动问题的解题方法
一般公式法: 一般公式法指速度、位移和速度关系三式.它们都是矢量式,使用时注意方向性.一般v0的方向为正向,其余与正方向相同者为正,与之相反者取负.
平均速度法:在匀变速直线运动中,平均速度有如下特点:
v中巾为中间时刻的瞬时速度,在解题时若能灵活运用,不但简便易行,而且省时、准确,能大大提高解题的速度和效率,
逆向思维法:把运动过程的“末态”作为“初态”的反向研究问题的方法.一般用于末态已知的情况,比如竖直上抛运动中所谓的对称性、可逆性就是如此.
图象法:应用图象,可把较复杂的问题转变为简单的数学问题解决.尤其是用图象定性分析,可避开繁杂的计算,快速找出答案.
巧选参考系法:一个物体的运动,相对不同的参考系,运动性质一般不同.通过变换参考系,可将运动简化.



一、运动的描述
第一章是高一物理的起始章节,跟初中物理相比,高中物理内容的深度与广度都有明显的增强,学生学习物理的方法也有所不同,物理学科对学生的理解、分析、推理、综合、应用等各方面的能力要求都较高.绝不能死记硬背有关物理概念和规律,而要全面理解其内涵与外延,做到真正理解和掌握.就本章的学习,要理解质点、加速度等重要概念;要充分认识矢量这一重要概念;再次就是要认识x-t、v-t图象的意义,并能用来解决简单的问题.
在学习过程中重点要认清四个关系:
1.时刻与时间间隔的关系
时间间隔能展示运动的一个过程,在时间轴上表示一段,时刻只能显示运动的一个瞬间,在时间轴上表示一点.对一些关于时间间隔和时刻的表述,要能够正确理解.如:第2s末、2s时、第2s初等均为时刻;2s内、第2s、第2s至第3s内……均为时间间隔.
2.路程与位移的关系
位移表示位置变化,用由初位置到末位置的有向线段表示,是矢量.路程是运动轨迹的长度,是标量.只有当物体做单向直线运动时,位移的大小才等于路程.一般情况下,路程≥位移的大小.
3.速度与速率的关系
二、匀变速直线运动的研究
在学习匀变速直线运动知识中一定要理解熟记公式及推论,并灵活应用解决问题.
1.公式
速度公式:v=v0+at
位移公式:
推导公式:
推论:
(1)匀变速直线运动的物体,在任两个连续相等的时间里的位移之差是个恒量,即
(2)匀变速直线运动的物体,在某段时间内的平均速度,等于该段时间的中间时刻的瞬时速度,即
.以上两推论在纸带处理中经常用到,要熟练掌握.
(3)
,某段位移的中间位置的瞬时速度公式(不等于该段位移内的平均速度).
可以证明,无论匀加速运动还是匀减速运动,都有
.
(4)初速度为零的匀加速直线运动(设T为等分时间间隔):
末速度为零的匀减速运动可以看作初速度为零的匀加速运动(逆向思维)
2.典型问题
(1)追及和相遇或避免碰撞的问题:此类问题一般有三种解法,解法一是对运动过程的分析,抓住两车间距有极值时速度应相等这一关键条件来求解;解法二是由位移关系得到一元二次方程,然后利用根的判别式来确定方程中各系数间的关系,这也是中学物理中常用的数学方法;解法三是通过巧妙地选取参照物,应用图象法和相对运动知识求解,利用相对运动的处理手段来使两车运动的关系变得简明.
关键在于掌握两个物体的位置坐标及相对速度的特殊关系.即速度相同时,两质点间距离最大或最小.基本思路:分别对两个物体研究,面出运动过程示意图,列出方程,找出时间、速度、位移的关系,建立相应的方程求解.解出结果,必要时可借助两质点的速度图象进行分析.在追赶过程中,速度相等是一个转折点:追者和被迫者速度v相等是能否追上、两者间的距离有极值、能否避免碰撞的临界条件,也就是隐含条件.
(2)相遇类问题的不同情景异同点.
①匀加速运动追及匀速运动,当二者速度相同时相距最远,
②匀速运动追及匀加速运动,当二者速度相同时追不上以后就永远追不上了.此时二者相距最近.
③匀减速直线运动追匀速运动,当二者速度相同时相距最近,此时假设追不上,以后就永远追不上了.
④匀速运动追匀减速直线运动,当二者速度相同时相距最远,
⑤匀加速直线运动追匀加速直线运动,应当以一个运动物体当参照物,找出相对速度、相对加速度、相对位移.
(2)相对运动问题:选地面或相对于地面静止的物体作为参考系,这样对物体运动的描述与我们平时的习惯相符.但在解决运动学问题时,同学们的思维不能僵化,因为同一道运动学问题,选取不同的参考系,对运动的描述以及问题解决的难易程度可能差别很大.智者化繁为简,灵活地选取合理的参考系,巧妙地解决有关的运动学问题是学生必须具备的能力.通常选取除地面外的物体(经常是运动的,且与研究对象有着一定的关联)来研究物体的运动就通俗地称为“相对运动”的解题思想.
如图1,甲球从离地面H高处 从静止开始自由下落,同时使乙球从甲球的正下方地面处做竖直上抛运动.欲使乙球上升到
处与甲球
相撞,则乙球上抛的初速度应为 多大?
如果选择地面为参考系,则甲做自由落体运动,下落高度为
,由运动学方程可得
;
乙做竖直上抛运动,若设乙球抛出的初速度为v,由运动学方程可得
两式联立解得
下面我们看看假如以自由下落的甲球为参考系,以向上为正方向,则乙球的初速度就为v相对=v0-0=v0向上,相对加速度为av相对=-g-(-g)=0,即乙将向上做匀速运动,则从抛出到两球相遇的时间为:
即等于甲自由落体的时间
可直接解得
对比发现选择相对运动系统中的物体,有时可以简化运动模型,匀速运动总比变速运动简洁吧.同学们可以自己通过实践来慢慢体会和有意识地熟练解题的方法,另外对本题同学们可以尝试选择乙物体为参考系,看看解题过程是否同样简洁.
3.匀变速直线运动问题的解题方法
一般公式法: 一般公式法指速度、位移和速度关系三式.它们都是矢量式,使用时注意方向性.一般v0的方向为正向,其余与正方向相同者为正,与之相反者取负.
平均速度法:在匀变速直线运动中,平均速度有如下特点:
v中巾为中间时刻的瞬时速度,在解题时若能灵活运用,不但简便易行,而且省时、准确,能大大提高解题的速度和效率,
逆向思维法:把运动过程的“末态”作为“初态”的反向研究问题的方法.一般用于末态已知的情况,比如竖直上抛运动中所谓的对称性、可逆性就是如此.
图象法:应用图象,可把较复杂的问题转变为简单的数学问题解决.尤其是用图象定性分析,可避开繁杂的计算,快速找出答案.
巧选参考系法:一个物体的运动,相对不同的参考系,运动性质一般不同.通过变换参考系,可将运动简化.

