几何折叠解读,核心问题探讨
白福清
[摘 ?要] 折叠是几何研究的重点内容,以其为背景命制的考题形式也较为多变,可以充分考查学生动态分析、问题转化、模型构建、知识综合等能力. 文章对折叠问题进行剖析,结合实例探究其中的核心问题,总结解题策略.
[关键词] 几何;折叠;性质;线段;面积;探究
问题综述
轴对称是初中几何的重要知识点,而以轴对称为基础进行知识考查的折叠问题在几何中有着重要的地位. 有些问题的轴对称特性隐藏较深,在解题时学生若不能充分挖掘,则容易陷入解题困境,难以获得解题突破口. 几何问题中,折叠问题具有代表性,常涉及角度分析、线段求值、面积解析、图形探究等. 同时以折叠性质为基础,综合圆的性质、三角形全等与相似、勾股定理等内容进行考查.
在备考复习时除了需要扎实基础,还需要把握几个解题关键点:一是找准图形折痕,确定图形的对称轴;二是明确折叠前后图形的对应元素,提取等量关系;三是合理利用几何折叠的关联性质,利用勾股定理、三角形相似来构建方程求解. 图形折叠问题可归为计算型和讨论型两类,实际解题时可结合相应的数学思想,巧用数形结合,合理转化简解.
类题探讨
几何折叠问题的形式较为多样,涉及众多考点,下面举例其中的三大核心问题,探讨突破思路,总结解题策略.
类型一:折叠中的角度
折叠前后对应角相等,故折叠变换中存在相应的等角关系,考查图形折叠中的角度是其问题之一. 求解时需要明晰折叠前后图形的对应角,结合图形内角、角相关定理,结合等角代换来推理计算.
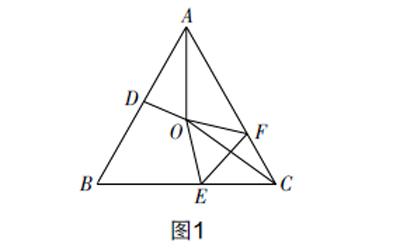
例1 ?如图1所示,△ABC为等腰三角形,已知AB=AC,∠BAC=50°,∠BAC的平分線AO与AB的中垂线相交于点O. 若点C沿着EF进行翻折刚好与点O相重合,则∠CEF的度数为______.
解析 ?本题目属于几何折叠中的角度计算题,除了涉及几何折叠外,还包含了角平分线、中垂线等几何知识,需要利用相应的几何性质来推导角度大小.
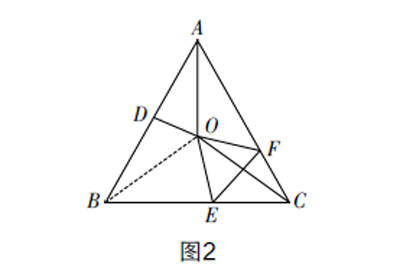
连接OB,如图2所示. 根据垂直平分的性质可知AO=BO,∠OAB=∠OBA,结合已知条件可得∠ABC=∠ACB=65°,由角平分线的性质可得∠BAO=∠CAO=25°,所以∠OBA=25°,∠OBC=40°. 推理可证△ABO≌△ACO,故BO=CO,∠OBC=∠OCB=40°. 根据折叠过程的轴对称性质可知OE=CE,∠OEF=∠CEF,从而有∠ECO=∠EOC=40°,则∠OEC=100°,所以∠CEF=50°.
评析 ?本题目主要考查几何折叠中角度的推导,在计算角度时用到了角平分线、线段中垂线、全等三角形的判定及性质等知识点. 折叠过程实则隐含着轴对称的性质,充分利用该性质可打开问题突破口.
类型二:折叠中的线段
求解图形折叠中的线段长度十分常见,也是折叠探究中的核心内容. 折叠前后的图形为全等图形,其中含有一些等长线段,因此分析时需要明晰折叠过程,合理利用几何定理来构建线段关系,如勾股定理、三角形相似性质等.
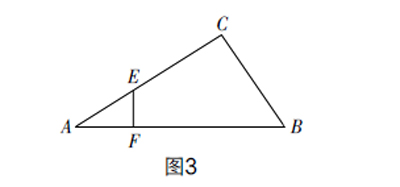
例2 ?如图3所示,在三角形纸片ABC中,有AB=40 cm,∠ACB=90°,∠A=30°,现将∠A进行折叠,使得点A落在AB边上的点D处,设折痕为EF,若所得△CDE为直角三角形,则线段AF的长为______.
解析 ?本题目属于常规的折叠问题,核心条件有两个:一是折叠后点A落在点D处,二是所得△CDE为直角三角形,前者可以利用折叠性质来提炼条件,后者由于没有明确具体的直角,显然需要加以讨论.
根据已知条件可推得BC=20 cm,由翻折特性可知AF=DF,∠A=∠EDF=30°,当∠EDC=90°时,如图4所示,则∠CDB=60°. 又∠B=60°,所以△BCD为等边三角形,BC=BD=20 cm,则AD=20 cm,从而有AF=10 cm.
当点B与点D重合时,∠C=90°,满足要求,如图5所示,此时△CDE为直角三角形,则点F为线段AB的中点,有AF= AB=20 cm.
综上可知,满足条件的AF长度有两个,分别为10 cm和20 cm.
评析 ?上述题目分析图形折叠背景下的线段长,由于没有设定直角三角形的直角情形,因此结合条件进行了分类讨论,这也是图形折叠中常见的多解分析方法. 在进行多解分析时需要充分采用数形结合的策略,结合直观的图像来讨论具体的问题情形,以轴对称特性为突破口来构建思路.
类型三:折叠中的面积
折叠问题具有一定的综合性,图形折叠后会出现新的几何图形,而分析这些图形的面积是常见的问题类型. 对于其中的规则图形可以直接结合面积公式来探究条件,而不规则图形则需要采用等面积转化的策略来求解. 具体分析时要充分利用折叠特性,提取等长线段,巧用等面积关系.
例3 ?如图6所示,四边形ABCD为矩形,已知AB和BC的长分别为2和3,点M是BC边上不与点B和C相重合的一个动点,设BM=x. 现将△ABM沿着AM进行折叠,使点B落在射线MP的点B′处,点E是边CD上的一点,设CE=y,再将△CME沿着ME进行折叠,使得点C落在射线MP的点C′处. 试求当y取到最大值时△C′ME的面积.
解析 ?本题目分析图形折叠中的几何面积,问题的特点有两个:一是进行了两次折叠,二是涉及最值分析. 因此求解时需要结合折叠特性建立与x、y相关的函数,利用函数性质确定y的最大值,再构建△C′ME的面积模型.
根据条件可知∠B=∠C=90°,则∠AMB+∠BAM=90°,根据折叠特性可得∠AMB′=∠AMB,∠EMC′=∠EMC,可推得∠BAM=∠EMC,进而有△ABM与△MCE相似,根据相似性质可得 = ,即 = ,整理可得y=- x2+ x=- x- 2+ ,当x= 时,y可取得最大值 ,即BM= 时CE= ,而CM=BC-BM= . 分析可知此时△C′ME的面积与△CME的面积相等,则S =S = ·CM·CE= ,即y取最大值时,△C′ME的面积为 .
评析 ?上述求解图形折叠中的几何面积,其特殊之处在于需要首先构建线段函数求解最值,然后进行等面积转化求解. 线段函数的构建方式有很多,常见的有利用勾股定理、三角形相似的线段比例性质. 需要注意折叠中的几何全等也是几何面积转化的重要方式,在求解时要灵活运用.
总结思考
图形折叠实则就是轴对称变换,是图形变换的一种方式,几何折叠虽然是一种动态变化的过程,但可以用静态的眼光来探索特性. 解题时需理解图形折叠前后元素的对应关系,掌握折痕的垂直平分特性,充分根据折叠情形来构建解题思路.
在实际教学中提出以下几点建议:一是充分展示折叠过程,使学生感知、体验图形折叠的动态变化过程,深刻理解其中的“不变”特性;二是关于折叠特性的几何关联,图形折叠是几何的重要研究内容,但其知识点并不独立,而是与其他几何定理紧密关联,因此在实际探究时需要引导学生挖掘折叠内涵,结合图形特性来构建知识体系;三是分类探究折叠问题,上述展示了图形折叠中的三大核心问题,实际折叠问题考查形式是多变的,教学中需要挖掘问题特点,反思转化方法,思考构建策略,总结解题经验,提升学生的解题思维.

