老曲新唱味更浓

    葛铁雷

    

    

    

    [摘 ?要] 初三中考数学专题复习历来是每年中考冲刺的关键一环，以专题的形式注重培养学生的数学思想和数学思维方法，此时学生已经过一轮复习，各知识点已基本了然于心，故怎样抓住学生的好奇心和求知欲，是每位初三教师须直面的问题.文章以“共顶点正方形中的线段关系”为例，探究初三数学专题复习课如何高效进行.

    [关键词] 共顶点;自主编题;核心素养

    初三中考数学专题复习历来是每年中考冲刺的关键一环，以专题的形式注重培养学生的数学思想和数学思维方法，此时学生已经过一轮复习，各知识点已基本了然于心，故怎样抓住学生的好奇心和求知欲，是每位初三教师须直面的问题.笔者2019年上半年应邀执教了一堂区复习研讨课，课题为“再探正方形——共顶点正方形中的线段关系”，现将教学过程整理成文，请各位同行指正.

    自主先学

    本环节安排在课前一天，以自主学习单的形式发放，当天不再布置其他数学作业，设置两个活动：

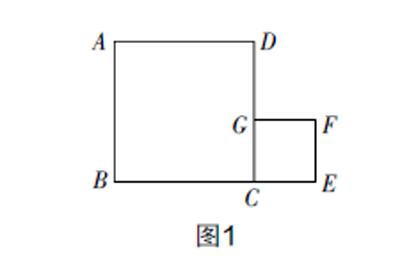
    活动1：现有一张矩形纸片，你能通过折叠的方式，得到一个正方形吗？剩余的部分还能折叠得到正方形吗？请说明理由，画出图形，并建构正方形知识框架图. （图1由学生自主构图得到）

    活动2：自主编题：将正方形GCEF绕点C旋转，请设计一道关于线段关系的解答题.比一比，谁的设计最精彩.

    “自主先学”是高效课堂的前提，传统的课堂以教师为主，教师牵着学生走，学生围着教师转，不仅教学效果差，也不利于学生健全人格形成和发展.“自主先学”，以学生为主体，设计了两个活动：活动1让学生自主建构知识体系;活动2自主设计题目，“自己创题，考验同伴”，激发学生的探究欲和进取心.上课当天早上，及时收回自主学习单，批阅学生的自主编题成果，选择典型问题在课堂展示.

    课堂展示

    本环节当堂进行，学生展示前一天“自主先学”的学习成果，并与同伴分享.下面是大多数学生设计出的一道题：

    学生编题成果1：如图2、图3，在正方形ABCD和GCEF中，线段BG，DE有什么关系？并证明你的结论.

    第一道学生编题，应该来说其实是学生回忆出的在初二正方形知识新授时的一道题，思维水平和层次是比较低的，两幅图都可由三角形BCG和三角形DCE全等，得到BG=DE，再由“8字形”模型得到BG⊥DE.显然对于初三后期思维水平训练是不够的，所以此处可以适时引导.

    抛出新的问题：既然BG和DE互相垂直，你能否通过这一特殊位置关系，找找其他线段的数量或位置关系，请独立思考后小组合作，设计一个新的问题.此时学生独立思考一段时间后，小组合作学习气氛浓郁，考虑到BG⊥DE，如果连接D，B，E，G四点，就可以得到一个对角线互相垂直的四边形，并最终形成了编题成果2：

    学生编题成果2：如图4，已知正方形ABCD和GCEF的边长分别是5，2，连接BE，DG，求BE2+DG2.

    成果2的难度明显有了提升，连接BD，EG，可用勾股定理证明出BE2+DG2=BD2+EG2，得出对角线互相垂直的四边形的性质：对角线互相垂直的四边形，对边的平方和相等.此时教师再抛出问题：成果2要求的问题，形式不够简约，老师想把它这样改，请尝试解决. （学生编题成果2改编）如图5，已知正方形ABCD和GCEF的边长分别是5，2，连接BE，DG，正方形GCEF绕着点C旋转，当D，G，F三点共线时，求BE的长.

    这道题的改编，教师直接给出，此时让课堂静了下来，学生静静地思考，并很快得到了问题的答案.教师继续引导：BG⊥DE始终成立，那么你能找到DE，BG交点的轨迹吗？能否就此点编制一道动态类题目？

    学生编题成果3：如图6，已知正方形ABCD和GCEF的边长分别是5，2，BG，DE相交于点O，当正方形GCEF绕着点C旋转时，求AO的最大值（最小值，或取值范围）.

    教师总结：刚才同学们的编题成果1、成果2、成果3，都是围绕共顶点正方形中的线段关系展开的，都利用旋转型全等的结论，三个成果组合在一起，都可以变成一道中考压轴题27题了，你们的能量超乎了老师的想象，真的是太棒了.适时表扬，积极评价，学生的干劲十足.

    评价完这组题后由另一学生展示出另一种类型的编题成果（上课前批阅学生自主学习单时已挑选好）.

    学生编题成果4：如图7，在正方形ABCD和GCEF中，连接BE，DG，过点C画CM⊥BE交DG于点N，求证DN=GN.

    学生独立思考后，进入小组合作学习，仍然不会解答的学生，由同伴来指导解决.采用“兵教兵”的方式——1号生讲给6号生听，2号生讲给5号生听，3号生讲给4号生听. 小组内已解决的，举手示意，并挑选一组学生上讲台展示，最先由最“差”的6号生讲，讲不下去后，再由5号生补充，积分递减.

    成果4，很好地建构了“K字形全等”，与前例的“旋转型全等”交相呼應.成果4画垂直可证平分，画平分可证垂直，示意图如图8.

    学生编题成果5：如图9，在正方形ABCD，GCEF中，连接AF，则=_______.

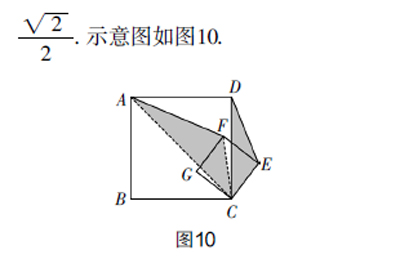
    这道成果题，另辟蹊径，又连接了另一种线段AF，从问题入手，学生很自然想到构造相似形去完成，从全等到相似，思维品质又上了新的台阶. 连接AC，利用“SAS”证明三角形ACF和三角形DEC相似，从而得出等于定值. 示意图如图10.

    总结提升

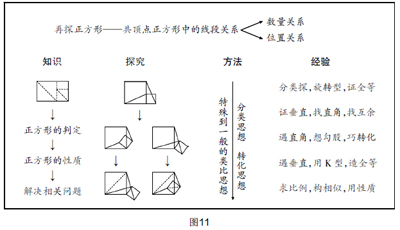
    如图11，总结提升，让学生的思维得以升华.

    课后反思

    1. 良好的学材是成功的一半

    美国著名数学教育家波利亚说：“一个专心的认真备课的教师能拿出一个有意义的但又不太复杂的题目，去帮助学生挖掘问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的领域.”本堂课从学生一个耳熟能详的引子出发，得出了一系列的学习成果，学生的思维能力、团队协作意识均得到了较好的提升. 所以我们在二轮复习时，教师一定要挑选好合适的专题、好的学材，让学生深入研究，时间紧，任务重，让学生把时间用在刀刃上.

    2. 要舍得花时间让学生自主创造

    著名数学家和数学教育家弗赖登塔尔任务数学的唯一正确方法是实行“再创造”，“立德树人”的根本任务需要我们去培养学生的数学核心素养，数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析，这些核心素养如何培养，“学生自主创造”就是一条有效的途径.不要担心学生创造不出什么好题来，学生的能量是不可估量的. 通过“自主创造”“同伴互考”等方式充分调动学生的求知欲，激发学生的兴趣——本例中都能编制压轴题了. 学生想学了，爱学了，自然会亲近数学，亲近数学老师，还愁学生学不好数学，拿不到高分吗？

    让我们潜心研究，“老曲新唱”打好二轮复习专题关，走向中考的成功！