追本溯源 拓展探究
林志森
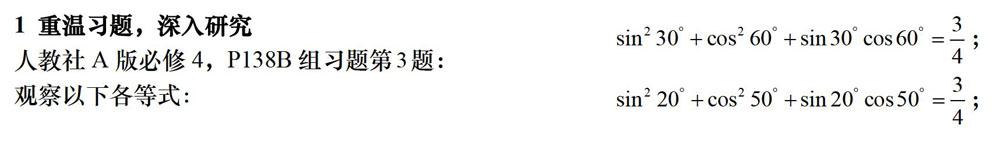

1重温习题,深入研究
人教社A版必修4,P138B组习题第3题:
观察以下各等式:
该题考查同角三角函数公式、二倍角公式等基础知识,考查运算求解能力、抽象概括能力、推理论证能力,考查特殊与一般思想、化归与转化思想.
2重新思考,意外收获
3追本溯源,一般拓展
由化简后的式子结构与余弦定理相似,类比推理联想到余弦定理.
从特殊情况归纳,到类比联想到余弦定理,得出一般结论,做到了追本溯源.
4一点感悟,激活教材
数学教材凝聚了编者的智慧和结晶,教材中的内容具有基础性、典型性和权威性,它是教师教学的基础和前提,也是命题的立足点.数学教材中的例题习题都是编者经过精心设计、反复揣摩后敲定的,大部分題目比较基础,入口浅,有利于学生夯实基础知识;同时,教材中的一些例题习题看似平淡无奇,却隐藏着精彩背景,可以进行深入挖掘与拓展.数学教学中,不仅仅要认真钻研教材,用好教材,还要进一步开发教材,拓展教学功能,挖掘教材的营养成分,让学习跳出题海,培养学生钻研精神,提高学习效率.
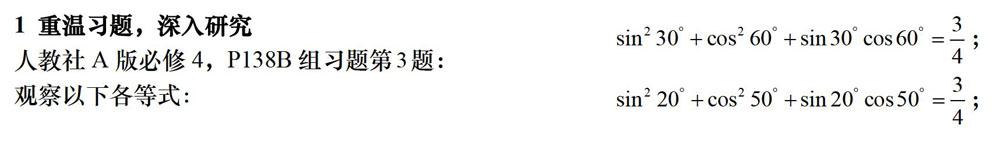

1重温习题,深入研究
人教社A版必修4,P138B组习题第3题:
观察以下各等式:
该题考查同角三角函数公式、二倍角公式等基础知识,考查运算求解能力、抽象概括能力、推理论证能力,考查特殊与一般思想、化归与转化思想.
2重新思考,意外收获
3追本溯源,一般拓展
由化简后的式子结构与余弦定理相似,类比推理联想到余弦定理.
从特殊情况归纳,到类比联想到余弦定理,得出一般结论,做到了追本溯源.
4一点感悟,激活教材
数学教材凝聚了编者的智慧和结晶,教材中的内容具有基础性、典型性和权威性,它是教师教学的基础和前提,也是命题的立足点.数学教材中的例题习题都是编者经过精心设计、反复揣摩后敲定的,大部分題目比较基础,入口浅,有利于学生夯实基础知识;同时,教材中的一些例题习题看似平淡无奇,却隐藏着精彩背景,可以进行深入挖掘与拓展.数学教学中,不仅仅要认真钻研教材,用好教材,还要进一步开发教材,拓展教学功能,挖掘教材的营养成分,让学习跳出题海,培养学生钻研精神,提高学习效率.

