模型思想视角下“角的比较与运算”设计研究
陈海烽
[摘 ?要] 文章以“角的比较与运算”为例,阐释模型思想这一视角在设计中的运用. 对于角度的和与差,抽象出有公共端点的三条射线组成的模型这个结构,进而继续模型化,可得到更一般的结构,那就是整体等于部分之和的模型.?摇此设计经过实践后取得了良好的教学效果.
[关键词] 模型思想;设计;实验
“角的比较与运算”是人教版《义务教育教科书·数学》七年级上册第四章第三节“角”的第二小节的第一课时,学生在此之前学习了线段的比较与运算、线段的中点,且已经知道了角的定义、角的表示方法和角的度量. 此内容是学生今后学习角平分线、角的代数运算等内容的奠基课,所以非常重要. 研究者在厦门市第六届课堂教学创新大赛中展示本节课,用模型思想的视角来演绎,取得了良好的教学效果,现整理成文,供大家讨论、交流.
对模型思想的再认识
《义务教育数学课程标准(2011年版)》(以下简称《课标》)中十大关键词对模型思想的定义是:“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径. 建立和求解模型的过程包括:从现实生活或具体情境中抽象出数学问题,用数学符号建立方程、不等式、函数等表示数学问题中的数量关系和变化规律,求出结果并讨论结果的意义. ”模型思想是一种基本的数学思想,是《课标》里明确提出的十个核心概念中唯一以“思想”冠名的概念.
沈文选指出,“数学模型可以描述为……运用适当的数学工具,得到的一个数学结构”“数学模型……也包括……数学概念、各种数学公式、方程式、定理、理论体系等”.
研究者主要是为了得到一个良好的数学结构,用数学的符号建立一个基本角度的和与差的运算模型.
教学设计
1. 教学目标设计
(1)通过动手实验、讨论、展示,知道角的比较大小的两种方法——度量法和叠合法,从中感悟角的和与差的运算模型.
(2)利用一副三角板拼凑角度,通过实验的观察和讨论,知道拼三角板的本质就是两个角度的和与差.
(3)通过几何画板的演示,抽象出具体角的和与差的基本模型,能从基本图形位置关系中提炼角度之间的和与差的数量关系模型.
(4)通过对基本模型进行不断变化的过程,让学生从特殊到一般,知道角度之间和与差的运算,能初步运用模型解决问题.
(5)通过基本模型的变式,提高学生关于角度和与差的运算能力.
2. 教学过程设计
(1)温故知新,引出课题
教师:三角板是我们的朋友,今天我们一起来“玩转三角板”.
问题1:你能说出老师手上这个三角形中这两个角的大小吗?
追问:你是如何知道的?
问题2:度量法要注意些什么呢?
追问:要知道这两个角的大小,除了度量法,还有别的方法吗?
问题3:你是如何想到叠合法的?是受什么得到的启发?角度的叠合要注意些什么?
问题4:你知道角的大小比较中的道理吗?
师生活动:学生回忆三角板的相关知识,通过操作、实验发现了度量法和叠合法,教师让学生展示和交流.
教师关注:对于学生的认知,教师给予相应的回应,同时引导学生通过类比的方法获知学生的最近发展区,引导学生从物理模型到数学图形的过渡.
设计意图?摇 从与学生相处多年的三角板入手,能让学生获得亲近感;从特殊角度之间的大小比较,过渡到一般角度的大小比较,能让学生第一次感知从特殊到一般,从而为抽象出角度的和与差的基本模型做准备.
(2)动手操作,探究新知
問题5:我们刚才比较了两个角度(60°和45°)之间的大小,你知道这两个角度之间差了多少度吗?你能否把差的角度拼出来?
追问1:你能否再用这副三角板拼叠出那些度数的角?这些角有什么规律?
追问2:为什么这些角都是15°的倍数?你能说出理由吗?
师生活动:学生动手操作,小组合作探究,师生归纳.
师生归纳:可以拼出很多的角. 还可以拼出15°,75°,105°,120°,135°,150°,165°,180°.
设计意图?摇 三角板的拼角游戏,能让学生对特殊的角度之间有一个良好的认识,能锻炼学生对角度大小的估计能力和动手操作能力,能加深学生对角的识别能力,且能让学生初步奠定“拼与和的运算对应,叠与差的运算对应”的经验基础.
(3)提炼模型,应用新知
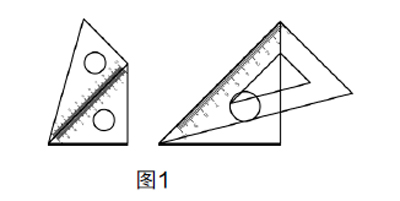
问题6:通过对三角板进行拼接,我们获得了不少角度. 下面我们继续观察拼出75°和15°这两个角度的图形. 如图1,老师的三角板和你们的“大小”不同,为什么拼叠出的角度是一样的?
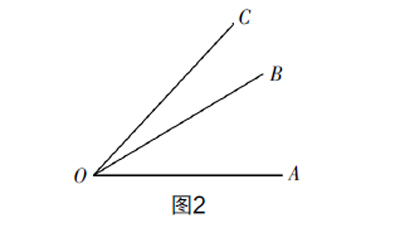
追问1:图1的两个图形和图2有什么地方是一致的?
追问2:老师将上述两种拼法图形化,然后将题一般化,获得如图2所示的模型. 你能告诉我它们之间的和差关系吗?
追问3:这个和差关系的模型能否用文字语言来描述?
追问4:这个模型能否用整体、部分的关系来描述?
设计意图?摇 从上一环节拼三角形的特殊角度出发,获知角度和与差的基本模型,使得教学衔接更加自然,促使学生从实物到图形到文字进而到语言之间的良好转化,引导学生从具体到抽象,加深对角度和与差的理解. 第二次从特殊到一般,直接抽象出现有的模型,引导学生对模型进行表达——有公共端点的三条射线就是对角度和与差的模型的最简图形表达. 接着,教师引导学生从整体到部分,提炼出更一般的加法模型,使得学生的认知能力有质的提升.
(4)变式训练,固化模型
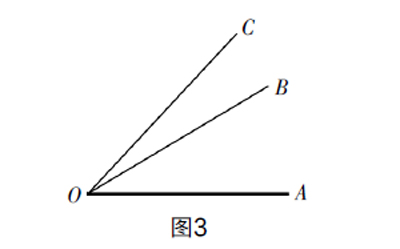
问题7:如图3,∠AOC=45°,∠AOB=30°,求∠BOC的大小.
变式1:如图3,∠AOC=45°,∠AOB=26°34′,求∠BOC的大小(此题系厦门中考题改编).
变式2:课本例1.
变式3:如图3,(几何画板演示拖动)∠AOC=180°,锐角∠AOB=x°,求∠BOC的大小(用含x的代数式表示).
变式4:已知∠AOC=45°,∠AOB=30°,求∠BOC的大小.
变式5:如图4,∠AOB=∠_____-∠_____=∠_____-∠_____,∠AOC=∠_____-∠_____=∠_____+∠_____.
变式6:你能根据图4写出结果等于∠BOD的和差算式吗?
变式7:如果老师再增加一条射线,如图5,你还能写出几个结果等于∠BOD的和差算式?
师生活动:教师示范,学生答题并展示.
教师关注:学生答题是否严谨、规范.
设计意图 ?摇从特殊角度的计算,过渡到一般角度的计算,再到式子的表达,再次体现了从特殊到一般,从具体到抽象. 为了对思维进行不断的提升,研究者从有配图到无配图,这一过程体现了分类讨论思想. 且计算时,不仅巩固了度、分、秒的运算,还将其与十进制的加减法进行类比,体现了类比思想.
(5)方法总结,优化结构
教师:我们一起来回顾一下本节课的学习方法.
问题8:对于角的大小比较,我们是如何学习的?
问题9:对于角的和差运算,我们是如何学习的?
追问:从学习过程中,我们可以获得什么样的学习经验?
师生活动:教师和学生共同回忆并整理本节知识的学习流程.
教师关注:学生的表现以及逻辑表达.
设计意图?摇 通过对整堂课的梳理,学生再次回忆学习过程,明晰研究流程,从中获得了学习经验,提高了对整节课的结构把握,同时内化为了自己的知识,能站在模型思想的角度看待数学问题,这有利于培养学生更加深邃的数学眼光.
教学反思
1. 动手实验,感知模型?摇
数学教育家波利亚曾指出,数学具有两个面,以欧几里得方向表现出来的数学看上去是一种系统演绎的科学,但在形成过程中的数学看上去却是一种实验性的归纳科学. 数学实验是学生在运用有关工具(如学具、计算机、数学软件等)时,在数学思维活动的参与下,通过手脑并用,借助观察、模仿、实验、猜想等手段获得体验,构建发展学生数学认知结构的素养型活动. 从引导学生观察图形入手,感知拼叠角度,进而感知角度的和与差的基本图形,这一认识不是书本或教师告知的,而是学生透过现象,发挥自己的洞察力分析得到的. 此处以发展学生的洞察力,寻求解决问题的方法为主要目标. 角度的拼叠再次让学生经历观察、比较、推理、交流等活动,进一步培养了学生的洞察力,发展了学生的创新意识. 学生的上课表现,说明学生对模型的感知是到位的.
2. 活用画板,抽象模型
《课标》指出:要加强信息技术在数学学习的整合. 本节课,学生通过三角板拼出各种角度,感知各个角度的变化情况,然后通过观察,得出本质——由公共端点的三条射线组成的模型. 研究者通过几何画板引导学生观察,让学生去除非本质的东西,抽象出有用的数学模型,体现了从具体到抽象的数学思想. 同时在变式3、变式4的教学过程中,研究者再用几何画板的功能,给予学生强烈的震撼,这能加深学生对模型的進一步理解.
3. 类比推理,同化模型
在本课的设计中,研究者用到了如下类比:一是角度的比较和线段的比较相类比,二是线段的和差运算和角度的和差运算相类比,三是角度的加减运算和十进制的加减运算相类比. 这些类比的本质就是同化,有利于学生数学素养的提升. 《课标》指出:数学素养是现代社会每个公民应该具备的基本素养. 其中的素养至少包含三个方面的含义,一是用数学的眼光审视生活;二是在生活中养成积累数学活动经验的习惯;三是在不断联系数学与生活的过程中自觉锻炼思维能力和应用能力. 本节课从学生最常见的三角板入手,让学生知道数学就在我们身边,而且可能就在我们经常忽视的地方存在着,需要我们重新去审视,引导学生用数学的眼光去审视三角板的各种用途. 同时就拼叠过程积累数学活动经验,抽象出有公共端点的三条射线这一基本角度和差数学模型,并将此模型加以应用,引导学生从比较抽象的问题中联想、转化为我们已经解决过的数学问题,以达到思维畅通.
4. 变式训练,活用模型
抽象出有公共端点的三条射线这一模型之后,研究者设置了几道题加以运用. 问题7是从特殊的角度入手,让学生体会到运算其实很简单,以增强学生学习的自信心. 教学过程中,变式1加入了不同单位的角度直接运算,此时的难点是60进制的体会. 等学生完成后,研究者分析讲解,接着通过几何画板进行动态演示,进入书本习题,即变式2,体现了一个动态的研究过程,以让学生掌握角的运算. 变式3是研究者给定了一个参数,让学生体会其与一元一次方程的关联;接着研究者将图撤掉,得到变式4,让学生在脑中画图,使得原有的经验得以升华. 而变式5和变式6则主要是训练学生将复杂图形化归为基本模型的能力.
结束语
对于“角的比较与运算”这一课,多数设计者没有从模型的角度去思考. 不少教师认为,这个问题比较简单,不值得花时间,于是往往通过大量的训练去强化角度的和差运算,甚至把这节课当成一堂习题课. 这种做法的背后其实存在着对一节课价值判断的问题,值得我们深思.

