关注解题反思，促进自主学习

    缪平

    

    

    

    [摘 ?要] 文章针对如何培养学生的解题反思能力进行了实践与研究，通过反思审题过程、反思解题结果、反思解题思想方法，让学生养成主动反思的习惯，使学生自主探索学习，从而提升学习能力，为可持续发展打下良好的基础.

    [关键词] 数学;审题;解题;反思;解题能力

    数学解题反思是在解题过后的再思考、再认识，达到逐步提升的一个过程. 我国最早的教育著作《学记》中说：“学然后知不足，教然后知困. 知不足，然后能自反也;知困，然后能自强也. ”在初中数学学习活动中，任何一个学生，不论其学习能力起点如何，其学习能力的提升大多数是通过数学解题来实现的. 随时进行反思，是提高数学学习效果的关键措施. 在新课程实施的今天，如何在教学活动中对学生数学解题反思能力进行有效的培养，已经成为当前教师进行新课改的一项重要任务.

    反思审题过程，确保解题的合理性和正确性

    审题不是把字面意思读一遍就结束了，而是要迅速准确地把握住题目的题表信息和题目的隐含信息.

    1. 反思是否读出了题表信息

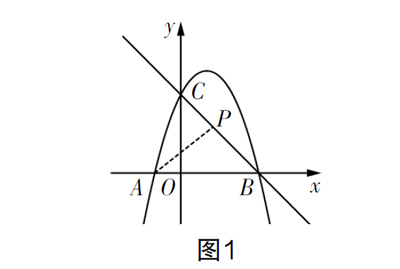
    例：如图1所示，直线y=-x+3与x轴，y轴分别交于点B，C，抛物线y=-x2+bx+c经过点B，C，点A是抛物线与x轴的另一个交点.

    （1）求抛物线的解析式;

    （2）若点P在直线BC上，且S=·S，求点P的坐标.

    认真审题，我们发现这一题强调的是“点P在直线BC上”，显然题目中的表层信息是要考虑点P在直线上的位置，要分类讨论点P可能在第一象限，可能在第二象限，当然由题意S=S，可否定点P在第四象限. 学会读出题中的表层信息可以减少题目漏解，确保解答的完备性.

    通过反思审题，学会读出表层信息，就是要能够根据题目的“字面”意义获取有利于解题的信息. 如已知一元二次方程有两个解，要考虑两个解是相等还是不相等. 再如，已知两个三角形相似，要注意是否存在不同点的对应关系. 两圆相切要考虑两圆有外切和内切，△ABC是等腰三角形，要分成三种情况讨论，①AB=BC， ②AB=AC，③BC=AC.

    2. 反思是否读出了题目的隐含信息

    例：已知x，x是关于x的方程x2-（m-1）x+2m=0的两根，且满足x+x=8，求m的值.

    分析：这题表面看似简单，由根与系数的关系可得，x+x=m-1，xx=2m，x+x=（x+x）2-2xx=（m-1）2-4m=m2-6m+1=8，解这个一元二次方程可求出m的值. 但这题要考虑用根与系数的关系的前提是解要存在，所以需要Δ≥0.

    解题时因审题不准，概念不清，忽视条件，套用相近知识，考虑不周或计算出错，难免产生这样或那样的错误. 审题是解题的基础，读懂题是正确、迅速解题的前提. 波利亚说：“最糟糕的情况是学生没有弄清问题就进行计算. ”事实上，这样的错误经常出现. 为此，在平时的教学中笔者注意引导学生分两步读题，第一步：每读一小部分，找出这句话的关键部分做上记号，同时思考由这部分我们可得出哪些信息，这样一小部分一小部分地读完整道题. 第二步：再快读整道题，找出整道题的重点，避开与解题无关的文字，直击主题.

    反思解题结果，查缺补漏，养成良好的解题习惯

    检验不是计算题的专利，学生的很多错误都是由于缺少检验而导致的，因此养成检验的习惯是学好数学的重要条件之一.

    1. 学会边算边验

    例：抛物线y=ax2+bx+c（a≠0）经过（0，1）和（2，3）两点.

    （1）如果拋物线的开口向下，对称轴在y轴的左侧，求a的取值范围;

    （2）若对称轴为x=-1，求抛物线的解析式.

    分析：这题的第一问错的学生非常多，原因是直接由抛物线的开口向下即得a<0，如果这样做，那就漏掉了条件“对称轴在y轴的左侧”，这时我们要细细品味这句话，千万不能急功近利. 在解题过程中可能会出现错误，这需要我们在解题时边算边验，一步一回头，争取一次做到位，防止无效劳动.

    2. 学会算完再验

    例：若关于x的一元二次方程（m-1）·x2+5x+m2-3m+2=0的常数项为0，求m的值.

    分析：m2-3m+2=0，可解得m=1，m=2，这时如果不再验算，那这道题就徒劳无功了. 这题的验算只需将m=1，m=2代入原方程，将m=1代入就会发现原方程不是一元二次方程了.

    解题后可对解题过程进行回顾和评价，对结论的正确性和合理性进行验证. 让学生学会验算，可以从不同角度，不同侧面去探讨解题结果是否正确，这对培养学生思维的灵活性、严密性有很大帮助. 养成良好的验算习惯，对培养学生良好的解题习惯非常重要.

    反思解题方法，提高综合解题能力

    数学知识有机联系纵横交错，解题思路灵活多变，解题方法途径繁多，但最终却能殊途同归. 学生在解题时往往满足于做出题目，而对自己解题方法的优劣却从来不加评价，作业中经常出现解题过程单一、思路狭窄、解法陈旧、逻辑混乱、叙述冗长、主次不分等不足，即使一次性解题合理正确，也未必能保证一次性解题就是最佳思路，最优最简捷的解法.

    1. 一题多解

    一题多解既可看到知识的内在联系、巧妙转化和灵活运用，又能开拓思维，让学生充分发挥自己的数学思维运用能力，找到问题的最优解法.？摇

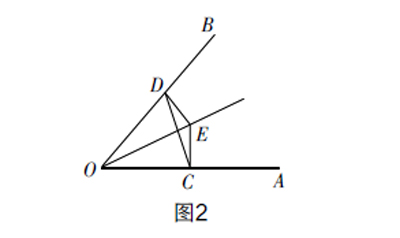
    例：如图2，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别是C，D.

    求证：（1）∠ECD=∠EDC;（2）OC=OD;（3）OE是线段CD的垂直平分线.

    解法1：利用△OCE≌△ODE，得到∠OED=∠OEC，再通过证明图中的两个小三角形全等来证明∠ECD=∠EDC;同样用三角形的全等来证明OE是线段CD的垂直平分线.

    解法2：利用角平分线的性质得到ED=EC，再由等边对等角得到∠EDC=∠ECD，继而得到∠ODC=∠OCD，再由等角对等边得到OC=OD;第三个问题直接由ED=EC，OC=OD得到OE是线段CD的垂直平分线.

    在肯定学生们答案的同时，让他们比较哪种方法最简便. 通过比较，激活了学生们的最优化解题意识，这样学生可以从中体会到学习乐趣，感受到自己在学习当中的主体地位，能清楚地意识到自己在学习中的创造和自学能力，极大地增强了他们学好数学的信心，更培养了他们的发散思维能力. 还要引导学生通过解题以后的反思，优化解题过程，总结解题经验，提炼可用于以后解题的方法.

    2. 反思归类，将类似题型作比较，找异同点，做到举一反三，融会贯通

    很多同学做题时做一题扔一题，从不归纳分析，只见树木不见森林，只要题型稍微一变，就束手无策. 笔者在平常的教学中注意帮助学生分析比较类似题型，发现它们之间的异同点，掌握规律，探求共性，再由共性指导我们去解决这类问题. 让学生能更深刻地理解类似题型，从而掌握一类问题的解法.

    例如在梯形中出现一腰上的中点时，连接顶点和这个中点并延长与另一底边相交构造全等三角形.

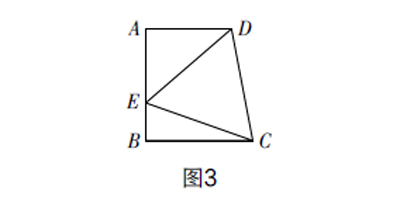
    例：如图1所示，在直角梯形ABCD中，AD∥BC，AB⊥BC，∠DCB=75°，以CD为一边的等边三角形DCE的另一顶点E在腰AB上

    （1）求∠AED的度数;

    （2）求证：AB=BC;

    （3）如图3所示，若F为线段CD上一点，∠FBC=30°，求的值.

    分析：本題的前两个问题学生基本可以解决，主要问题在第三问，由结果求的值易想到构造相似三角形求值，单看这一题构造起来就不太容易，如果能够和上面两题类比，我们就会发现它们的共同点是有梯形的腰的中点，这时我们作如图4所示的辅助线，利用△DFG≌△CFB可得=1.

    因此，教师必须引导学生进一步反思，分析解题方法的优劣，优化解题过程，努力寻找解决问题的最佳方案. 通过这一过程，开阔学生的视野，使学生的思维逐渐朝着多开端、灵活、精细和新颖的方向发展，在对问题本质的认识不断深化的过程中提高学生的概括能力，以促使学生形成一个系统性强、着眼于相互联系的数学认知结构，在更高层次更富有创造性地去学习、摸索、总结，使自己的解题能力更胜一筹.

    认知心理学认为：“学生学习的过程是一个把教材知识结构转化为自己认知结构的过程. ”有效的解题练习可以推动这个过程的顺利完成. 在解题活动中，学生养成良好反思能力，对养成学生自主学习的良好品质具有重要的推动和促进作用.