双模型结合进一步降低预测均方根误差和均方根相对误差的方法
吴雪梅 刘志强 张天龙 李华


摘 要 前期研究工作提出了以预测均方根相对误差最小为回归目标的方法(Minimization of prediction relative error,MPRE),它能使得预测结果的均方根相对误差更小。偏最小二乘法(Partial least squares,PLS)是以预测均方根误差为回归目标,能使得预测结果的均方根误差更小。基于多模型结合的思想,提出将MPRE与PLS相结合的双模型结合多元校正方法。本方法步骤为:(1) 分别采用MPRE与PLS法对校正集建模;(2) 计算阈值;(3)分别采用已建立好的MPRE与PLS模型进行预测;(4)将预测结果与阈值进行比较,得到预测结果。通过对酒精的近红外光谱与汽油紫外光谱进行定量分析结果表明,本方法可进一步减小预测均方根误差与相对误差。
关键词 双模型; 多元校正; 均方根相对误差; 均方根误差
1 引 言
随着现代大型仪器的使用,多元校正方法被广泛应用于分析化学领域【1~3】。目前常用的多元校正方法主要有经典最小二乘法(Classical least-squares,CLS)、主成分回归法(Principal component regression,PCR)、偏最小二乘法(Partial least squares,PLS)等线性多元校正方法及人工神经网络法(Artificial neural network, ANN)、非线性PLS等非线性多元校正方法【7,8】。无论是线性多元校正方法,还是非线性多元校正方法,均方根误差(Root-mean-square error of prediction, RMSEP)通常被用作多元校正的评价指标【9~11】。换言之,在这些多元校正方法中,其校正的目标是预测样本组分的均方根误差最小,其建模的代价函数是预测误差平方和。采用该代价函数可在一定程度上使预测组分的绝对误差尽可能小。在组分值动态范围较小时,现有的线性或非线性多元校正方法能取得较为理想的结果。但是当组分值动态范围较大时,如组分值范围为1~100 mmol/L时,虽然采用现有的多元校正方法能使得预测均方根误差较小(如预测均方根误差为0.5 mmol/L),在实际应用中,较小的预测均方根误差相对较大组分值而言相对误差较小,预测数据可靠性高,但是相对于较小组分值而言,预测相对误差非常大,甚至超过100%,预测数据可靠性变差。
本研究组前期工作提出了一种能使预测均方根相对误差最小化的方法(Minimization of prediction relative error,MPRE)【12】。MPRE法选择反向传播神经网络(Back-propagation artificial neural network, BP-ANN))【13】为回归方法,通过改变预测器输出来实现预测结果均方根相对误差最小的目的。PLS是以均方根误差最小为回归目标的多元校正方法,1983年Wold and Martens将该方法引入化学领域后,由于其性能突出被广泛应用于多元校正分析中【14】。本研究利用MPRE法与PLS法的双模型结合多元校正方法,进一步减小预测均方根误差与相对误差。
2 基本理论
2.1 MPRE法简介
预测均方根相对误差最小化方法(MPRE)【12】采用BP神经网络建模。与常见的神经网络建模方法相同,MPRE将光谱信息作为输入信息,采用经典的训练方法对网络进行训练。为了实现预测均方根相对误差最小,在MPRE方法中,对输出值进行了调整,以组分信息的对数值作为输出:
文献已从理论上证明,对建模输出值采用组分值的对数,MPRE可实现预测均方根相对误差最小的目标; 虽然MPRE法与PLS法的预测结果的RMSEP值相当,但MPRE法能获得更小的均方根相对误差。
预测均方根误差RMSEP定义为:
2.2 双模型结合方法
2.2.1 基本思想 从文献的理论分析与实验结果可知,采用常规的多元校正方法只能实现RMSEP最小,难以实现预测均方根相对误差Pre最小,其原因是对低含量组分预测时,预测误差与组分值的比值较大,从而导致总体预测均方根相对误差较大。MPRE方法能减小低含量组分的预测误差,保证预测均方根相对误差较小,但是由于其功能设计时只保证预测均方根相对误差最小,并未考虑预测均方根误差RMSEP,故在组分值较大时,其预测误差也较大,甚至超过常规多元校正方法。从文献的实验结果还可看出,MPRE与PLS的RMSEP相当,但预测均方根相对误差Pre却存在明显差别。从统计学角度来看,在组分值较小时MPRE法预测绝对误差较小,当组分值较大时PLS法预测相对误差较小。如果将MPRE法与PLS法等常规校正算法相结合,在组分值较小时,采用MPRE预测结果,在组分值较大时采用常规校正算法(如PLS)预测结果,那么最终预测均方根相对误差与预测均方根误差均可能进一步减小。
2.2.2 阈值确定 从基本思想可知,双模型结合方法的关键是确定一个合适的阈值g,当采用MPRE预测结果小于阈值g时,选用MPRE法预测结果,反之选用PLS等常规校正算法的预测结果。
假设已知MPRE法取得的预测均方根相对误差为Pre,PLS等常规多元校正方法预测均方根误差为RMSEPs。显然阈值g的选择应满足如下条件:对于组分值为g的样本而言,MPRE的预测均方根误差RMSEP1与常规多元校正方法预测均方根误差RMSEPs2相等。
RMSEP1=gPre=RMSEP2 (7)
由式(7)可求得阈值:
g=RMSEp2pre(8)
在实际预测中,如果实验数据较多,可将数据分为校正集、验证集和预测集。此时,RMSEP2即为验证集的预测均方根误差,Pre为验证集的预测均方根相对误差。如果没有大量数据,可将数据分为校正集和预测集。此时,由于不知道待测光谱的具体组分值,RMSEP2与Pre值无法获得,这两个参数可以分别采用常规校正算法的校正均方根误差(Root-mean-square error of calibration, RMSEC)与MPRE法中间层确定时计算的预测相对误差来代替。
2.2.3 双模型结合方法步骤 双模型结合法步骤为: 分别采用MPRE法与PLS法对校正集建模;由公式(8)确定阈值g; 分别采用已建立好的MPRE与PLS模型进行预测,设预测结果分别为p1与p2;如果p1
与文献相同,为了验证所提方法在预测单组分样品、同时预测多组分样品、在样品存在组分值为0时的预测性能,同时,也为了说明算法对于不同光谱数据的适应性,实验中选择了两组不同类型的数据。
数据A 酒精的近红外光谱测量数据。酒精的浓度范围为:0.02~0.61(体积比,间隔0.01)共60个样本,由VERTEX 70傅里叶变换近红外光谱仪(布鲁克公司)测量各溶液的光谱。实验中,溶液按浓度从低到高排列,在建模与预测时,从第2个样品开始,每隔2个样品选一个样品作为预测集样品,其余样品作为校正集样品。
数据B 这是一组在网上公开的汽油的紫外光谱数据。实验中采用了其中名为“gasoil”的这组数据。下载网址为:http://myweb.dal.ca/pdwentze/downloads.html, Data Set #3。该数据共有115个样品的组分信息和光谱数据。根据样品提供者建议,采用前70个样品作为校正集样品,后续44个样品为预测集样品,最后一个为奇异值,在实验中不予使用。在这组数据中,组分2和3的组分值范围较宽,便于验证所提方法的性能。
4 结果与讨论
在实验中,PLS_toolbox(V5.5)用于建立PLS模型。建模时采用留一交叉检验法确定因子数,对数据集A确定的因子数是3,对数据集B确定的因子数为4。
MPRE法采用MATLAB 2006a编写完成。同文献,神经网络的输入和输出采用的是autoscale预处理方法,神经网络的中间层传递函数为logsig函数,输出层传递函数为purelin函数,对数据集A确定的中间层神经元数为2,对数据集B确定的中间层神经元数为3。回归过程的训练目标误差设置为0。训练的最大迭代次数设置为5000。对于数据B,其组分值中含有0,因此MPRE建模与预测时分别选用式(3)与式(4)进行处理,且f值设定为0.001。
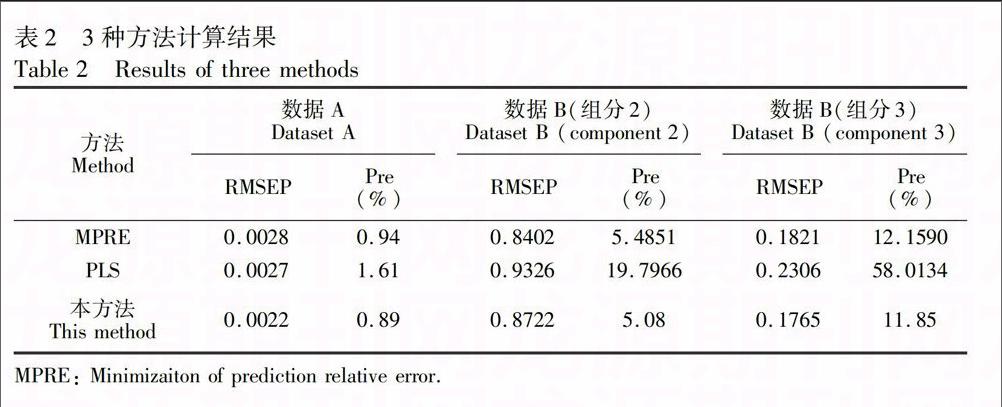
根据双模型结合方法步骤,阈值确定结果见表1。预测均方根误差与预测均方根相对误差统计结果见表 2。
实验结果表明,对于数据A,采用双模型结合算法后,预测结果的预测均方根误差与预测均方根相对误差均比MPRE法与PLS法低;对于数据B,第二组分的预测均方根误差介于MPRE法与PLS算法之间,但预测均方根相对误差小于MPRE法与PLS算法,第三组分的预测均方根误差与预测均方根相对误差均低于MPRE法与PLS法。从理论上讲,采用双模型结合校正算法预测结果的预测均方根误差与预测均方根相对误差均应比MPRE法与PLS法低,但是在实际计算中,一方面由于预测误差具有一定的随机性;另一方面阈值选取中重要参数RMSEP与Pre受到数据量小的限制,采用建模时RMSEC与选择中间层时确定的预测均方
根误差代替,使得阈值g不够准确;最终导致数据B组分二的预测均方根误差大于基本方法预测均方根误差。如果通过大量实验,准确地确定RMSEP与Pre两个参数,那么采用双模型结合算法将会以更大概率取得更优的预测结果。
5 结 论
双模型结合多元校正方法是一个多模型选择算法,当采用MPRE法预测结果低于阈值时,选用MPRE法结果,反之选用PLS法预测结果。该方法充分利用了MPRE法对低含量组分值预测准确与PLS法对高组分预测相对误差较小的优点,可同时减小预测均方根相对误差与预测均方根误差,适用于组分值具有较宽范围的多元校正。
References
1 Silva M A M, Ferreira M H, Braga J W B, Sena M M. Talanta, 2012, 89: 342-351
2 Beebe K R, Kowalski B R. Anal. Chem., 1987, 59(17): 1007A-1017A
3 NI Yong-Nian, CAO Dong-Xia. Chem. J. Chinese Universities, 2006, 27(6): 1048-1050
倪永年, 曹东霞. 高等学校化学学报, 2006, 27(6): 1048-1050
4 Zhou Y, Cao H, Hu J, Yu S, Zhao Q, Li X, Ju L. Instrum. Sci. Technol., 2011, 39(4): 394-405
5 Ns T, Martens H. J. Chemometr., 1988, 2(2): 155-167
6 BI Yan-Lan, REN Xiao-Na, PENG Dan, YANG Guo-Long, ZHANG Lin-Shang, WANG Xue-De. Chinese J. Anal. Chem., 2013, 41(9): 1366-1372
毕艳兰, 任小娜, 彭 丹,杨国龙, 张林尚, 汪学德. 分析化学, 2013, 41(9): 1366-1372
7 Long J R, Gregoriou V G, Gemperline P J. Anal. Chem., 1990, 62(17): 1791-1797
8 Malthouse E C, Tamhane A C, Mah R S H. Comput. Chem. Eng., 1997, 21(8): 875-890
9 Li Y, Shao X, Cai W. Talanta, 2007, 72(1): 217-222
10 Shao X, Bian X, Cai W. Anal. Chim. Acta, 2010, 666(1): 32-37
11 Nakagawa H, Tajima T, Kano M, Kim S, Hasebe S, Suzuki T, Nakagami H. Anal. Chem., 2012, 84(8): 3820-3826
12 Wu X, Liu Z, Li H. Anal. Methods, 2014, 6(12): 4056-4060
13 Mitchell T M. Mach. Learn., 1997: 81-127
14 Zhang M H, Xu Q S, Massart D L. Anal. Chem., 2005, 77(5): 1423-1431



摘 要 前期研究工作提出了以预测均方根相对误差最小为回归目标的方法(Minimization of prediction relative error,MPRE),它能使得预测结果的均方根相对误差更小。偏最小二乘法(Partial least squares,PLS)是以预测均方根误差为回归目标,能使得预测结果的均方根误差更小。基于多模型结合的思想,提出将MPRE与PLS相结合的双模型结合多元校正方法。本方法步骤为:(1) 分别采用MPRE与PLS法对校正集建模;(2) 计算阈值;(3)分别采用已建立好的MPRE与PLS模型进行预测;(4)将预测结果与阈值进行比较,得到预测结果。通过对酒精的近红外光谱与汽油紫外光谱进行定量分析结果表明,本方法可进一步减小预测均方根误差与相对误差。
关键词 双模型; 多元校正; 均方根相对误差; 均方根误差
1 引 言
随着现代大型仪器的使用,多元校正方法被广泛应用于分析化学领域【1~3】。目前常用的多元校正方法主要有经典最小二乘法(Classical least-squares,CLS)、主成分回归法(Principal component regression,PCR)、偏最小二乘法(Partial least squares,PLS)等线性多元校正方法及人工神经网络法(Artificial neural network, ANN)、非线性PLS等非线性多元校正方法【7,8】。无论是线性多元校正方法,还是非线性多元校正方法,均方根误差(Root-mean-square error of prediction, RMSEP)通常被用作多元校正的评价指标【9~11】。换言之,在这些多元校正方法中,其校正的目标是预测样本组分的均方根误差最小,其建模的代价函数是预测误差平方和。采用该代价函数可在一定程度上使预测组分的绝对误差尽可能小。在组分值动态范围较小时,现有的线性或非线性多元校正方法能取得较为理想的结果。但是当组分值动态范围较大时,如组分值范围为1~100 mmol/L时,虽然采用现有的多元校正方法能使得预测均方根误差较小(如预测均方根误差为0.5 mmol/L),在实际应用中,较小的预测均方根误差相对较大组分值而言相对误差较小,预测数据可靠性高,但是相对于较小组分值而言,预测相对误差非常大,甚至超过100%,预测数据可靠性变差。
本研究组前期工作提出了一种能使预测均方根相对误差最小化的方法(Minimization of prediction relative error,MPRE)【12】。MPRE法选择反向传播神经网络(Back-propagation artificial neural network, BP-ANN))【13】为回归方法,通过改变预测器输出来实现预测结果均方根相对误差最小的目的。PLS是以均方根误差最小为回归目标的多元校正方法,1983年Wold and Martens将该方法引入化学领域后,由于其性能突出被广泛应用于多元校正分析中【14】。本研究利用MPRE法与PLS法的双模型结合多元校正方法,进一步减小预测均方根误差与相对误差。
2 基本理论
2.1 MPRE法简介
预测均方根相对误差最小化方法(MPRE)【12】采用BP神经网络建模。与常见的神经网络建模方法相同,MPRE将光谱信息作为输入信息,采用经典的训练方法对网络进行训练。为了实现预测均方根相对误差最小,在MPRE方法中,对输出值进行了调整,以组分信息的对数值作为输出:
文献已从理论上证明,对建模输出值采用组分值的对数,MPRE可实现预测均方根相对误差最小的目标; 虽然MPRE法与PLS法的预测结果的RMSEP值相当,但MPRE法能获得更小的均方根相对误差。
预测均方根误差RMSEP定义为:
2.2 双模型结合方法
2.2.1 基本思想 从文献的理论分析与实验结果可知,采用常规的多元校正方法只能实现RMSEP最小,难以实现预测均方根相对误差Pre最小,其原因是对低含量组分预测时,预测误差与组分值的比值较大,从而导致总体预测均方根相对误差较大。MPRE方法能减小低含量组分的预测误差,保证预测均方根相对误差较小,但是由于其功能设计时只保证预测均方根相对误差最小,并未考虑预测均方根误差RMSEP,故在组分值较大时,其预测误差也较大,甚至超过常规多元校正方法。从文献的实验结果还可看出,MPRE与PLS的RMSEP相当,但预测均方根相对误差Pre却存在明显差别。从统计学角度来看,在组分值较小时MPRE法预测绝对误差较小,当组分值较大时PLS法预测相对误差较小。如果将MPRE法与PLS法等常规校正算法相结合,在组分值较小时,采用MPRE预测结果,在组分值较大时采用常规校正算法(如PLS)预测结果,那么最终预测均方根相对误差与预测均方根误差均可能进一步减小。
2.2.2 阈值确定 从基本思想可知,双模型结合方法的关键是确定一个合适的阈值g,当采用MPRE预测结果小于阈值g时,选用MPRE法预测结果,反之选用PLS等常规校正算法的预测结果。
假设已知MPRE法取得的预测均方根相对误差为Pre,PLS等常规多元校正方法预测均方根误差为RMSEPs。显然阈值g的选择应满足如下条件:对于组分值为g的样本而言,MPRE的预测均方根误差RMSEP1与常规多元校正方法预测均方根误差RMSEPs2相等。
RMSEP1=gPre=RMSEP2 (7)
由式(7)可求得阈值:
g=RMSEp2pre(8)
在实际预测中,如果实验数据较多,可将数据分为校正集、验证集和预测集。此时,RMSEP2即为验证集的预测均方根误差,Pre为验证集的预测均方根相对误差。如果没有大量数据,可将数据分为校正集和预测集。此时,由于不知道待测光谱的具体组分值,RMSEP2与Pre值无法获得,这两个参数可以分别采用常规校正算法的校正均方根误差(Root-mean-square error of calibration, RMSEC)与MPRE法中间层确定时计算的预测相对误差来代替。
2.2.3 双模型结合方法步骤 双模型结合法步骤为: 分别采用MPRE法与PLS法对校正集建模;由公式(8)确定阈值g; 分别采用已建立好的MPRE与PLS模型进行预测,设预测结果分别为p1与p2;如果p1
与文献相同,为了验证所提方法在预测单组分样品、同时预测多组分样品、在样品存在组分值为0时的预测性能,同时,也为了说明算法对于不同光谱数据的适应性,实验中选择了两组不同类型的数据。
数据A 酒精的近红外光谱测量数据。酒精的浓度范围为:0.02~0.61(体积比,间隔0.01)共60个样本,由VERTEX 70傅里叶变换近红外光谱仪(布鲁克公司)测量各溶液的光谱。实验中,溶液按浓度从低到高排列,在建模与预测时,从第2个样品开始,每隔2个样品选一个样品作为预测集样品,其余样品作为校正集样品。
数据B 这是一组在网上公开的汽油的紫外光谱数据。实验中采用了其中名为“gasoil”的这组数据。下载网址为:http://myweb.dal.ca/pdwentze/downloads.html, Data Set #3。该数据共有115个样品的组分信息和光谱数据。根据样品提供者建议,采用前70个样品作为校正集样品,后续44个样品为预测集样品,最后一个为奇异值,在实验中不予使用。在这组数据中,组分2和3的组分值范围较宽,便于验证所提方法的性能。
4 结果与讨论
在实验中,PLS_toolbox(V5.5)用于建立PLS模型。建模时采用留一交叉检验法确定因子数,对数据集A确定的因子数是3,对数据集B确定的因子数为4。
MPRE法采用MATLAB 2006a编写完成。同文献,神经网络的输入和输出采用的是autoscale预处理方法,神经网络的中间层传递函数为logsig函数,输出层传递函数为purelin函数,对数据集A确定的中间层神经元数为2,对数据集B确定的中间层神经元数为3。回归过程的训练目标误差设置为0。训练的最大迭代次数设置为5000。对于数据B,其组分值中含有0,因此MPRE建模与预测时分别选用式(3)与式(4)进行处理,且f值设定为0.001。
根据双模型结合方法步骤,阈值确定结果见表1。预测均方根误差与预测均方根相对误差统计结果见表 2。
实验结果表明,对于数据A,采用双模型结合算法后,预测结果的预测均方根误差与预测均方根相对误差均比MPRE法与PLS法低;对于数据B,第二组分的预测均方根误差介于MPRE法与PLS算法之间,但预测均方根相对误差小于MPRE法与PLS算法,第三组分的预测均方根误差与预测均方根相对误差均低于MPRE法与PLS法。从理论上讲,采用双模型结合校正算法预测结果的预测均方根误差与预测均方根相对误差均应比MPRE法与PLS法低,但是在实际计算中,一方面由于预测误差具有一定的随机性;另一方面阈值选取中重要参数RMSEP与Pre受到数据量小的限制,采用建模时RMSEC与选择中间层时确定的预测均方
根误差代替,使得阈值g不够准确;最终导致数据B组分二的预测均方根误差大于基本方法预测均方根误差。如果通过大量实验,准确地确定RMSEP与Pre两个参数,那么采用双模型结合算法将会以更大概率取得更优的预测结果。
5 结 论
双模型结合多元校正方法是一个多模型选择算法,当采用MPRE法预测结果低于阈值时,选用MPRE法结果,反之选用PLS法预测结果。该方法充分利用了MPRE法对低含量组分值预测准确与PLS法对高组分预测相对误差较小的优点,可同时减小预测均方根相对误差与预测均方根误差,适用于组分值具有较宽范围的多元校正。
References
1 Silva M A M, Ferreira M H, Braga J W B, Sena M M. Talanta, 2012, 89: 342-351
2 Beebe K R, Kowalski B R. Anal. Chem., 1987, 59(17): 1007A-1017A
3 NI Yong-Nian, CAO Dong-Xia. Chem. J. Chinese Universities, 2006, 27(6): 1048-1050
倪永年, 曹东霞. 高等学校化学学报, 2006, 27(6): 1048-1050
4 Zhou Y, Cao H, Hu J, Yu S, Zhao Q, Li X, Ju L. Instrum. Sci. Technol., 2011, 39(4): 394-405
5 Ns T, Martens H. J. Chemometr., 1988, 2(2): 155-167
6 BI Yan-Lan, REN Xiao-Na, PENG Dan, YANG Guo-Long, ZHANG Lin-Shang, WANG Xue-De. Chinese J. Anal. Chem., 2013, 41(9): 1366-1372
毕艳兰, 任小娜, 彭 丹,杨国龙, 张林尚, 汪学德. 分析化学, 2013, 41(9): 1366-1372
7 Long J R, Gregoriou V G, Gemperline P J. Anal. Chem., 1990, 62(17): 1791-1797
8 Malthouse E C, Tamhane A C, Mah R S H. Comput. Chem. Eng., 1997, 21(8): 875-890
9 Li Y, Shao X, Cai W. Talanta, 2007, 72(1): 217-222
10 Shao X, Bian X, Cai W. Anal. Chim. Acta, 2010, 666(1): 32-37
11 Nakagawa H, Tajima T, Kano M, Kim S, Hasebe S, Suzuki T, Nakagami H. Anal. Chem., 2012, 84(8): 3820-3826
12 Wu X, Liu Z, Li H. Anal. Methods, 2014, 6(12): 4056-4060
13 Mitchell T M. Mach. Learn., 1997: 81-127
14 Zhang M H, Xu Q S, Massart D L. Anal. Chem., 2005, 77(5): 1423-1431

