运用极值法与赋值法解决电学问题的能力的研究

    石磊

    

    

    

    初中物理电学中的一些题用通常的方法解非常烦琐甚至无法解出，而运用数学极值法，则能迎刃而解.特别是在定性分析某些物理量的变化时，将收到事半功倍的效果.极值法是通过把某个物理量推向无限大或无限小后对问题作出分析和判断.赋值法是将题目中比较复杂、抽象的条件，赋给具体的合理的数值，然后对数值进行分析、处理，从而解决问题的一种方法.下面就这两种方法进行研究.

    一、极值法

    在初中物理解题过程中，有些题用一般的方法解比较烦琐，而用极值法常常能收到立竿见影、事半功倍的效果.

    例1如图1所示，开关S接位置1时，电流表示数为0.2A.当开关S接位置2时，电流表示数的可能值在A到A之间.

    解析：这是一道结合串联电路的特点考查欧姆定律的应用而又构思独特的试题.对电路的分析不是解答本题的难点所在，本题难点在于如何得出等量关系，并且灵活应用极限法进行分析.通过解决本题应注意体会数学知识与物理知识的紧密结合.由电路可知，开关接1时，R?1与R串联，由欧姆定律可列出关系式;开关接2时，R?2与R串联，同理由欧姆定律列出方程式.因电压保持不变，故可以得出I与R的关系式，由极限法分析方程式可得出结论.

    解：当开关接位置1时，由欧姆定律得：

    U=0.2（R?1+R）

    当开关接位置2时，由欧姆定律得：

    U=I（R?2+R）

    因电压值不变，故可得：

    0.2A（8Ω+R）=I（10Ω+R）

    因R未知，故R可能为从0到无穷大的任意值，当R=0时，I=0.2A-0.04A=0.16A.

    当R取无穷大时，I无限接近于0.2A.

    故电流值可以从0.16A到0.2A.

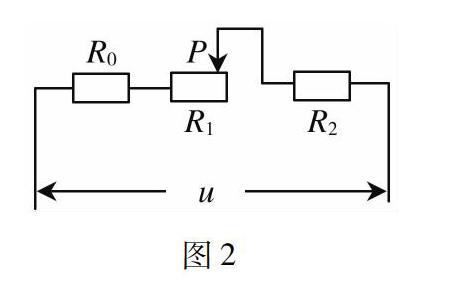
    例2如图2所示，当变阻器的滑片P置于某一位置时，R?1、R?2两端的电压分别为U?1和U?2，当滑片P置于另一位置时，R?1、R?2两端的电压分别为U?1和U?2，若ΔU?1=|U?1-U′?1|，ΔU?2=|U?2-U′?2|，则（）.

    A.ΔU?1>ΔU?2

    B.ΔU?1<ΔU?2

    C.ΔU?1=ΔU?2

    D.无法判断ΔU?1和ΔU?2哪个大

    解析：本题用数学上的比差法或比商法虽能得出结论，但计算量很大，若能想到用极值法，问题可很快解决.假想变阻器的最大电阻为无穷大，滑片P先置于最左端，这时R?1=0，U?1=0，U?2=UR?0+R?2·R?2

    U′?1≈U，U′?2≈0，

    ΔU?1=|U?1-U′?1|=|0-U|=U，

    ΔU?2=|U?2-U′?2|=U?2

    ΔU?1>ΔU?2.所以選A.

    极值法是中学物理解题方法中最为重要的方法之一，对于很多只需作定性分析的题，运用这种方法解题省略了繁琐的运算，用很简单的推理即可得到结果.但这种方法常被中学生由于“想不到”而忽略.因此要引起重视，在教学中有意识地引导学生用极值法解题，从而扩展学生的思维.

    二、赋值法

    例3如图3所示，电源电压恒定，已知R?1∶R?2=2∶1.当开关S闭合时，电流表A?1与A?2的读数之比为（）.

    A.1∶3B.3∶1

    C.2∶3D.3∶2

    解析：电源电压U=12V，R?1=12V，R?2=6V.则通过R?1的电流为I?R?1=UR?1=1A;电流表A?1的读数I?A?1=UR?2=2A;电流表A?2的读数为I?A?2=1A+2A=3A.所以，电流表A?1与A?2的读数之比为2∶3，故答案为选项C.

    通过以上例可见，利用赋值法解物理选择题快捷且准确.它不仅能使抽象的定量研究具体化，而且还能使一些定性研究的问题定量化，因而易被学生接受.