万有引力定律要点例析
张统勋


一、熟悉两个重要定律
1.开普勒行星运动定律
(1)开普勒第一定律(又叫轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
第一定律告诉我们,尽管各行星的轨道大小不同,但它们有共同规律.
(2)开普勒第二定律(又叫面积定律):对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积。
第三定律反映了行星公转周期跟轨道半长轴之间的依赖关系.椭网轨道半长轴越长的行星,其公转周期越大;反之,其公转周期越小.其中常数k与行星无关,只与太阳有关。
例1 火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知 (
)
A.太阳位于木星运行轨道的中心
B.火星和木星绕太阳运行速度的大小始终相等
C.火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方
D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积
解析
火星和木星在各白的椭网轨道上绕太阳运动,速度的大小不可能始终相等,选项B错误;太阳在这些椭圆的一个焦点上,选项A错误;在相同时间内,某个确定的行星与太阳连线在相同时间内扫过的面积相等,选项D错误,只有选项C正确。
答案C
(3)公式适用条件:此公式适用于质点间的相互作用。当两物体间的距离远远大于物体本身的大小时,物体可视为质点。均匀的球体可视为质点,r是两球心间的距离.一个均匀球体与球外一个质点间的万有引力也适用,其中r为球心到质点间的距离。
(4)万有引力定律的“四性”
①普遍性:万有引力不仅存在于太阳与行星、地球与月球之间,宇宙间任何两个有质量的物体之间都存在着这种相互吸引的力。
②相互性:两个有质量的物体之间的万有引力是一对作用力和反作用力,总是满足大小相等、方向相反、作用在两个物体上。
③宏观性:地面上的一般物体之间的万有引力比较小,与其它力比较可忽略不计,但在质量巨大的天体之间,或天体与其附近的物体之间,万有引力起着决定性作用。
④特殊性:两个物体之间的万有引力只与它们本身的质量和它们间的距离有关,而与所在空间的性质无关,也与周围是否存在其它物体无关。虽然是牛顿由天体的运动规律得出的,但牛顿又将它推广到了宇宙中的任何物体,适用于计算任何两个质点间的引力,选项A错误;当两个物体间的距离趋近于0时,两个物体就不能视为质点了,万有引力公式不再适用,选项B错误;两物体间的万有引力也符合牛顿第三定律,选项C正确;公式中引力常量G的值是卡文迪许在实验室里用实验测定的,而不是人为规定的,选项D错误。
答案C
二、熟悉卫星的运动特点
1.地球同步卫星的特点
2.极地卫星和近地卫星
(1)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖。
(2)近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s。
(3)两种卫星的轨道平面一定通过地球的球心。
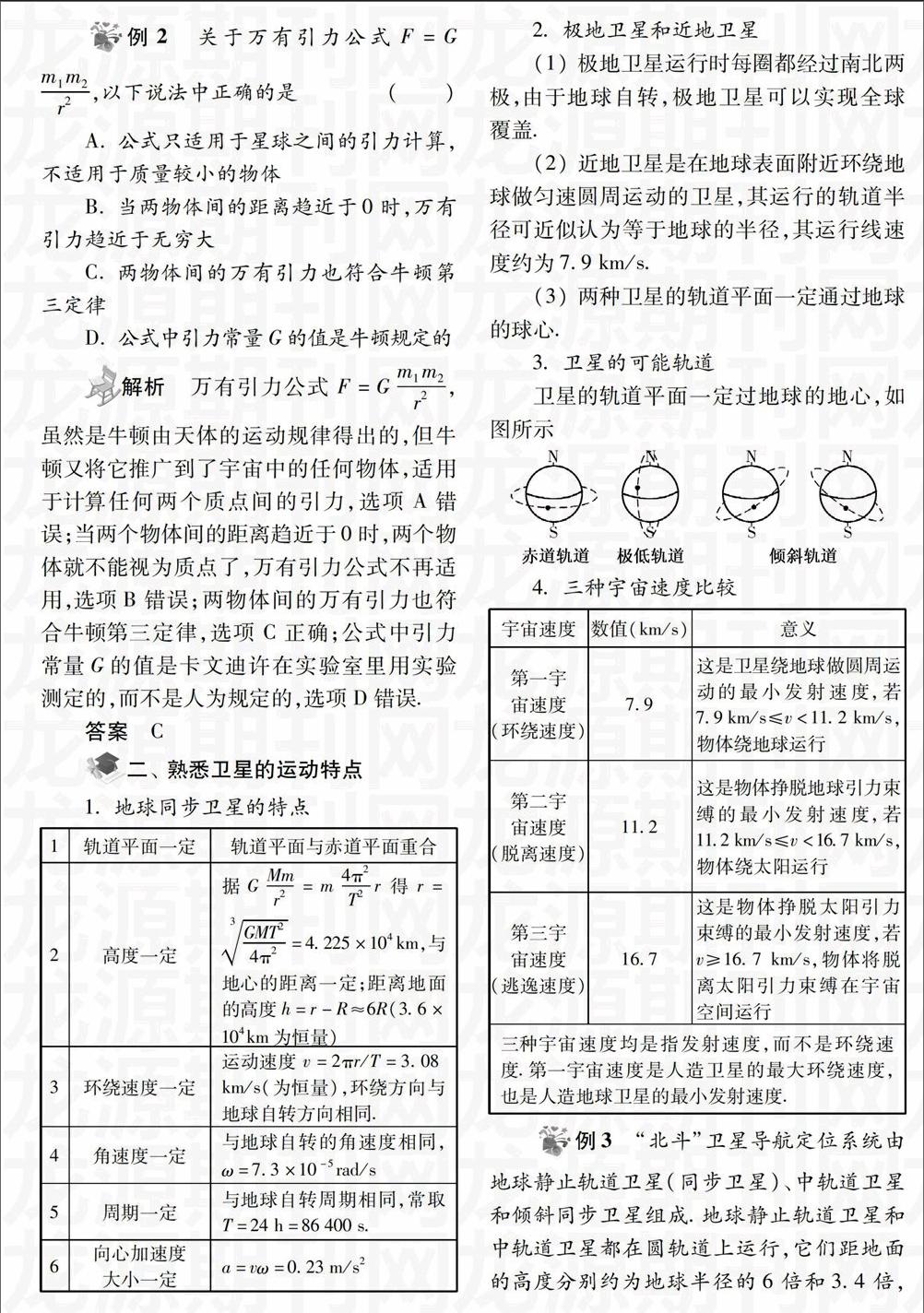
3.卫星的可能轨道
卫星的轨道平面一定过地球的地心,如图所示
4.三种宇宙速度比较
例3“北斗”卫星导航定位系统由地球静止轨道卫星(同步卫星)、中轨道卫星和倾斜同步卫星组成,地球静止轨道卫星和中轨道卫星都在圆轨道上运行,它们距地面的高度分别约为地球半径的6倍和3.4倍,下列说法中正确的是
(
)
A.静止轨道卫星的周期约为中轨道卫星的2倍
B.静止轨道卫星的线速度大小约为中轨道卫星的2倍
C.静止轨道卫星的角速度大小约为中轨道卫星的1/7
D.静止轨道卫星的向心加速度大小约为中轨道卫星的1/7
2.卫星运行参量的分析问题
卫星的各物理量随轨道半径变化的规律
例6“嫦娥一号”探月卫星绕地运行一段时间后,离开地球飞向月球。如图所示是绕地飞行的三条轨道,1轨道是近地圆形轨道,2和3是变轨后的椭圆轨道。A点是2轨道的近地点,B点是2轨道的远地点,卫星在轨道1的运行速率为7.7 km/s,则下列说法中正确的是
(
)
4.双星问题
绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示,双星系



一、熟悉两个重要定律
1.开普勒行星运动定律
(1)开普勒第一定律(又叫轨道定律):所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上。
第一定律告诉我们,尽管各行星的轨道大小不同,但它们有共同规律.
(2)开普勒第二定律(又叫面积定律):对任意一个行星来说,它与太阳的连线在相等的时间内扫过相等的面积。
第三定律反映了行星公转周期跟轨道半长轴之间的依赖关系.椭网轨道半长轴越长的行星,其公转周期越大;反之,其公转周期越小.其中常数k与行星无关,只与太阳有关。
例1 火星和木星沿各自的椭圆轨道绕太阳运行,根据开普勒行星运动定律可知 (
)
A.太阳位于木星运行轨道的中心
B.火星和木星绕太阳运行速度的大小始终相等
C.火星与木星公转周期之比的平方等于它们轨道半长轴之比的立方
D.相同时间内,火星与太阳连线扫过的面积等于木星与太阳连线扫过的面积
解析
火星和木星在各白的椭网轨道上绕太阳运动,速度的大小不可能始终相等,选项B错误;太阳在这些椭圆的一个焦点上,选项A错误;在相同时间内,某个确定的行星与太阳连线在相同时间内扫过的面积相等,选项D错误,只有选项C正确。
答案C
(3)公式适用条件:此公式适用于质点间的相互作用。当两物体间的距离远远大于物体本身的大小时,物体可视为质点。均匀的球体可视为质点,r是两球心间的距离.一个均匀球体与球外一个质点间的万有引力也适用,其中r为球心到质点间的距离。
(4)万有引力定律的“四性”
①普遍性:万有引力不仅存在于太阳与行星、地球与月球之间,宇宙间任何两个有质量的物体之间都存在着这种相互吸引的力。
②相互性:两个有质量的物体之间的万有引力是一对作用力和反作用力,总是满足大小相等、方向相反、作用在两个物体上。
③宏观性:地面上的一般物体之间的万有引力比较小,与其它力比较可忽略不计,但在质量巨大的天体之间,或天体与其附近的物体之间,万有引力起着决定性作用。
④特殊性:两个物体之间的万有引力只与它们本身的质量和它们间的距离有关,而与所在空间的性质无关,也与周围是否存在其它物体无关。虽然是牛顿由天体的运动规律得出的,但牛顿又将它推广到了宇宙中的任何物体,适用于计算任何两个质点间的引力,选项A错误;当两个物体间的距离趋近于0时,两个物体就不能视为质点了,万有引力公式不再适用,选项B错误;两物体间的万有引力也符合牛顿第三定律,选项C正确;公式中引力常量G的值是卡文迪许在实验室里用实验测定的,而不是人为规定的,选项D错误。
答案C
二、熟悉卫星的运动特点
1.地球同步卫星的特点
2.极地卫星和近地卫星
(1)极地卫星运行时每圈都经过南北两极,由于地球自转,极地卫星可以实现全球覆盖。
(2)近地卫星是在地球表面附近环绕地球做匀速圆周运动的卫星,其运行的轨道半径可近似认为等于地球的半径,其运行线速度约为7.9 km/s。
(3)两种卫星的轨道平面一定通过地球的球心。
3.卫星的可能轨道
卫星的轨道平面一定过地球的地心,如图所示
4.三种宇宙速度比较
例3“北斗”卫星导航定位系统由地球静止轨道卫星(同步卫星)、中轨道卫星和倾斜同步卫星组成,地球静止轨道卫星和中轨道卫星都在圆轨道上运行,它们距地面的高度分别约为地球半径的6倍和3.4倍,下列说法中正确的是
(
)
A.静止轨道卫星的周期约为中轨道卫星的2倍
B.静止轨道卫星的线速度大小约为中轨道卫星的2倍
C.静止轨道卫星的角速度大小约为中轨道卫星的1/7
D.静止轨道卫星的向心加速度大小约为中轨道卫星的1/7
2.卫星运行参量的分析问题
卫星的各物理量随轨道半径变化的规律
例6“嫦娥一号”探月卫星绕地运行一段时间后,离开地球飞向月球。如图所示是绕地飞行的三条轨道,1轨道是近地圆形轨道,2和3是变轨后的椭圆轨道。A点是2轨道的近地点,B点是2轨道的远地点,卫星在轨道1的运行速率为7.7 km/s,则下列说法中正确的是
(
)
4.双星问题
绕公共圆心转动的两个星体组成的系统,我们称之为双星系统,如图所示,双星系

