基于APOS理论视域下初中数学概念课的有效教学

    王卫东

    

    

    

    [摘? 要] 文章以建构主义APOS数学学习理论为依据，以“合并同类项”数学概念课教学为例，深入探究了促进学生概念深层次理解的策略，提出了“创设思维刺激模式，引入概念”“生活化类比归纳，认识概念”“辨析关键属性，建构概念”“深化关键属性，应用并形成新概念”“迁移概念图式，整合概念”等策略，以引领学生全方位感知概念、活用概念，不断同化概念，有效发展学生的数学思维.

    [关键词] APOS理论;初中数学;概念

    数学概念是学生理解数学定理、数学公式、法则，进行数学判断、推理、归纳等活动的基础和前提，而初中学生思维主要以感性思维、形象思维为主，加之数学概念本身具有的抽象性，致使部分学生对数学概念的理解含糊不清，难以自我建构其数学意义. 在探索解题方式时往往也不能从基本概念入手进行分析，从而影响了学生对概念知识的整体学习效果. 因此，笔者以建构主义APOS数学学习理论为依据，深入探究促进学生概念深层次理解的策略，以引导学生全方位感知概念、活用概念，不断同化概念，有效地发展学生的数学思维.

    基于APOS理论视域下的初中数学概念教学

    根据APOS理论，如果让学生经过操作、过程、对象等思维阶段，一般情况下学生就能厘清问题情境，就能在反思、建构的基础上形成图示，而初中阶段各种概念的获得都是从相应的感知入手的，都需要学生经过大量的实例，并通过总结、归纳、证明等过程形成概念. 而基于APOS理论视域下的初中数学概念教学，实质上，APOS理论为初中数学概念提供了理论视角，其最大的特征就是阶段性，结合APOS理论并研读新课标，初中数学概念新授课教学可分为概念引入、认识、建构、应用、小结等主要阶段[1].

    APOS理论视域下“合并同类项”概念教学策略

    1. 创设思维刺激模式，引入概念

    引导学生主动参与课堂教学是揭示概念形成过程、深刻理解概念的基础，鉴于初中学生感性思维占主导地位，因此，教师应合理安排课堂情境，采用生活实例、联系类比、数学活动、情境问题等多种引入方式，并呈现丰富的、通俗化的概念背景材料，介绍数学概念的起源，帮助学生由感性认识逐渐向理性认识过渡.

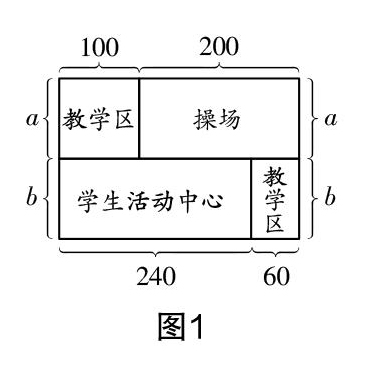
    例如，引入“合并同类项”概念时，为了刺激学生从“潜在”认识向“直观”思维感受转变[2]，笔者加入了必要的生活元素，创设了如下的思维刺激模式：如图1所示，试求该新校区总面积是多少.

    实质上，学生充分思考后，从不同层面上提出了对该问题的解决方案：一是从图形的格局上分析，计算得出新校区的总面积为（100+200）a+（240+60）b;二是从个体上分析，计算得出新校区的总面积为100a+200a+240b+60b;三是从整体上分析，计算得出新校区的总面积为（100+200）（a+b）. 然后，笔者要求学生思考这些代数式之前有什么联系和区别，并从面积相等的视角引导学生得出如下等式，即（100+200）a+（240+60）b=100a+200a+240b+60b=（100+200）（a+b），进而帮助学生引入本节课的主题，感受100a+200a对应（100+200）a等“分类”“合并”的思维模式.

    2. 生活化类比归纳，认识概念

    结合数学思维对概念有初步的认识是远远不能满足教学目标的，在学生充分感受、体验概念的基础上，教师应引导学生深入解读概念的内涵和外延，鼓励学生反思上述操作对象特征，并通过比较、归纳、总结等方式整合上述思维操作，最终形成独立完整的概念. 在具体教学实践中，教师应通过“是什么”“为什么”“怎么做”等提问形式，类比分化刺激模式的特征，将生活化问题类比分化到具体数学问题上来.

    例如，在组织学生学习“合并同类项”概念时，为了体会分类的简化问题功能，笔者通过“图书超市里面的书籍是如何分类的”“药店里面的药品是如何分类的”“教师是如何区别不同年级的学生”等具体生活问题，要求学生反思日常生活中为什么要进行分类，怎样才能做到科学分类，如果将图书超市里面放置的书籍抽象成为以下单项式，是否还可以进行分类：-2019，240b，7x2，0.5x2y，-9mn，2020，2ab，17mn3. 然后引导学生以小组为单位，组织学生思考、归纳上述刺激模式的共同特征，鼓励学生大胆猜想，应用数学语言表示上述分类标准. 例如，综合学生猜想，上述分类可以从系数、字母、字母次数等方面进行分类. 最后，总结得出概念中的关键属性，归纳出同类项的概念. 值得一提的是，对于一些未发现规律的学生，教师应适当地通过提示的方式组织学生探索，并为了有效验证学生是否真正理解同类项的概念可以设置一些例题. 例如，笔者根据学生实际，让学生利用所学知识判断-8，0，4是否是同类项，并说明判断的理由.

    3. 辨析关键属性，建构概念

    为了明晰概念，进一步在理解的基础上建构概念，教师应引导学生不断反思上述概念精细化的特征，并对设计到的关键词句，或者是图形符号等进行检验、辨析概念. 例如，在辨析同类项关键属性时，笔者设计了如下题目，要求学生辨析以下单项式哪些是同类项：①x，y;②a2b，ab2;③-3pq，3pq;④abc，ac;⑤a2，a3;⑥3x3y2，-y2x3;⑦23，32.

    值得一提的是，当学生在辨析同类项概念出现偏差时，教师应通过正面和反面例子加强师生互动，帮助学生厘清在判断同类项时，同类项与单项式的字母顺序、字母系数无关，从而将同类项从过程阶段转化为后续的对象阶段.

    4. 深化关键属性，应用并形成新概念

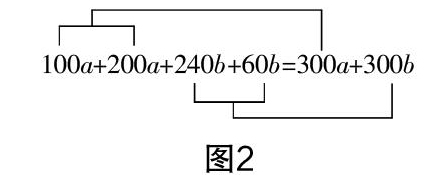
    为了进一步巩固、深化所学概念，教师应鼓励学生将上述思维过程视作为一个整体，将所获得概念的特征应用于各种特定的数学运算之中，并设置相关变式题目使学生能够从真正意义上理解概念的内涵和外延. 例如，笔者以课前所描述的100a+200a+240b+60b=（100+200）a+（240+60）b为例，通过如图2所示的图示引导学生理解合并同类项就是将两个以上的同类项合并为一项，从而引出“合并同类项”这一新概念.

    同时，为了认识合并同类项这个新概念，教师还应创设一些新问题进一步组织学生思考合并同类项这个新概念. 例如，笔者要求学生进一步说明合并同类项的依据是什么，在具体合并过程中应注意哪些注意事项，并引导学生总结出“一变二不变”的合并同类项法则. 最后，创设了如下问题要求学生独自解决. 在此期间，笔者及时对有困难的学生给予个别化指导.

    （1）请合并以下同类项：①-9x2y3+5x2y3;②5ab2+ab2-17ab2;③-7n3m5-23n3m5.

    （2）判断以下合并同类项是否正确，并说明理由：①3a+2b=5ab;②5y2-2y2=3;③4x3y2-2x2y=2xy.

    5. 迁移概念图式，整合概念

    為了进一步深度应用所学概念，帮助学生更高层次的加工、整合、提炼、建立思维图式，达到举一反三的目的，教师应将鼓励学生带着问题思考，有效地将已有知识与问题解决时思维突破过程进行关联和衔接. 同时，要求学生以本节课程的收获为主题，要求学生绘制概念学习过程图，激励学生发散创造性思维.

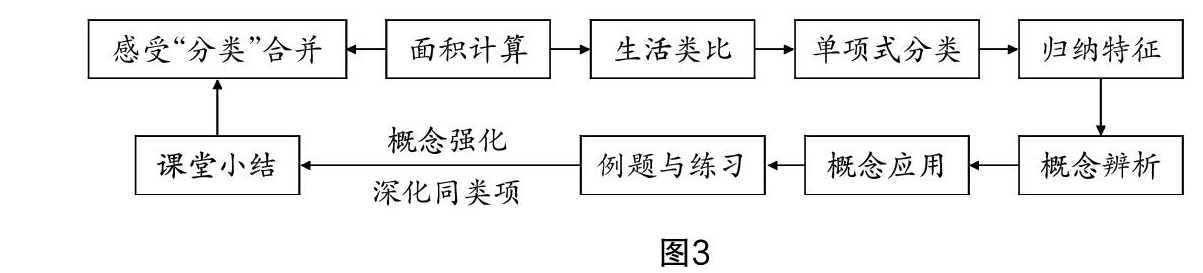
    如在小结“合并同类项”概念时，笔者要求学生将有关加法的运算律、合并同类项本身视作为认知整体，归纳概括提出合并同类项的策略及注意事项，并以本节课程的收获为主题，引导学生最终绘制如图3所示的合并同类项概念学习过程图.

    总之，初中阶段各种概念的获得都是从相应的感知入手的，都需要学生经过大量的实例，并通过总结、归纳、证明等过程形成概念. 数学概念的教学实践中，教师应抛弃死板灌输概念的理念，从教学内容和学生实际出发，引导学生联系生活实际，有效为学生的概念学习搭建平台，引领学生全方位感知概念，活用概念，不断同化概念，有效发展学生的数学思维.

    参考文献：

    [1]丁晓军. 关注学生认知过程，促进数学概念建构——基于APOS学习理论的教学思考[J]. 数学教学通讯，2019（05）.

    [2]卜以楼. 意识唤醒：揭示数学本质的有效策略——以苏科版课标教材“合并同类项”教学为例[J]. 中学数学，2013（06）.