把握主线类比探究，归纳性质素养提升

    尤方成

    

    

    

    [摘 ?要] “不等式的性质”是学生学习有理数大小比较、等式、数轴等基础上的知识深化，在教学设计时需要把握大纲要求，结合教学重点设计主线，采用合理的方式完成新知教授. 文章将深入分析“不等式的性质”内容，开展教学环节的设计探讨与反思.

    [关键词] 不等式;性质;类比;应用

    “不等式的性质”是初中数学七年级下册的重要教学内容，其中的性质定理是基本数量关系学习的基础，也为后续的解不等式和不等式组的解集提供了理论依据，因此该部分内容具有极高的教学意义，下面对其内容及环节设计进行探讨.

    关于教学内容的分析

    《课程标准》明确指出要求结合实例引导学生自主探索不等式的基本性质，深刻认识不等式的三条基本性质，并能准确利用性质来解决现实问题，同时学习其中的数学语言，培养学生的核心素养. 上述内容对“不等式的性质”的教学提出了两方面的要求：一是使学生掌握性质，二是培养学生的核心素养，尤其是语言能力. 基于该内容，结合学生的认知能力提出以下几点思路建议：

    1.不等式的性质教学需要采用探究式的教学方式，使学生经历知识的探究过程，自主总结形成性质，提升学生的探究能力.

    2.不等式与数轴之间有着一定的关联，教学时需要采用类比的方式，通过数形结合的方式强化学生对定理的认识.

    3.不等式性质的学习是为了解决问题，在完成性质总结后有必要开展性质的应用探究，通过对具体问题的分析来提升学生的应用能力.

    关于教学环节的设计

    基于上述的内容分析，在教学“不等式的性质”时需要考虑知识探究、类比教学、语言强化、性质应用等几个关键点，因此教学中可以按照“情景引入—类比探究—语言强化—拓展应用”的教学主线，完成不等式的“现实抽象→性质总结→知识应用”的过渡转换. 下面基于教学主线思考环节设计.

    设计环节（一）——情景设计，课题引出

    在生活中存在众多的不等式问题及现象，因此设计具体的活动，从中抽象不等式更能提高学生的学习热情，同时使学生深刻感受“知识源于生活”的内涵，可以设计如下情景活动.

    情景活动：课前请大家准备一个圆和正方形纸板，如果我们知道两个纸板的周长均为l，思考如何比较圆形和正方形的面积大小.

    引问1：圆的半径和正方形的边长分别是多少？

    引问2：圆和正方形的面积如何表示？

    引问3：结合经验可判断出两者的面积哪个大？

    引問4：除了利用分数知识外，还有哪些方法来解释？

    教学中首先引导学生利用图形的周长和面积公式构建相应的模型，即周长为l时，圆的面积为，而正方形的面积为. 然后结合知识经验“周长相等时，圆的面积最大”学生可以判断出圆的面积大于正方形的面积，即>. 此时需要教师进一步引导学生思考如何解释这一结论，在之前学生已经掌握了分数的相关知识，能够通过比较分母的大小来得出结论，课题引入时只需要让学生思考还有哪些方法解释结论即可.

    设计环节（二）——类比研究，认识符号

    不等式性质学习的基础是对不等式的符号有着充分的认识，因此在探究性质前需要类比认识不等符号“≥”和“≤”. 首先给出温度图（图1）和零件设计图（图2），使学生尝试使用不等符号来表示温度的变化范围和零件的合格尺寸. 然后在此基础上引导学生思考不等符号所具有的类似性质，完成表1的填写.

    类比温度变化和尺寸表示，学生可以较为直观地认识不等式的符号，并对其性质意义有一个初步的了解，从而完成不等式符号的语言学习.

    设计环节（三）——类比探究，性质学习

    不等式的三大性质是本章节教学的重点，也是难点所在. 考虑到其性质较为抽象，在探究过程中可以充分把握不等式与等式之间的关联，类比学习完成不等式性质的归纳，同时利用数轴的直观性来完成性质的验证.

    类比活动：完成表2的填写.

    在教学中设计如上填表活动，学生通过数的大小比较很容易就可以发现其中隐含的规律，此时教师就可以引导学生对其加以归纳，并用文字语言概括. 考虑到上述性质是类比总结所得，因此教学中十分有必要对结论进行验证.

    1. 性质1验证

    对于性质1——不等式两边加（或减）同一个数（或式子），不等号的方向不变，根据结论可知如果a>b，则a±c> b±c，需验证a>b时，a+c>b+c.

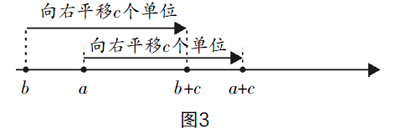
    验证活动：请同学们绘制数轴，在数轴上根据a>b取a和b点的位置，然后将两点的位置分别向右平移c个单位，如图3所示.

    思考1：结合数轴思考a+c和b+c的大小.

    思考2：数轴上点的位置移动后不等符号是否需要改变.

    2. 性质3验证

    而对于不等式性质3的数轴验证，需要利用到数轴上的原点，教学时首先让学生思考是否需要将零排除在外，然后进行如下引导.

    引问1：对于a>b时，若将不等号左右两边同乘以-2，则-2a和-2b在数轴上如何取点？

    引问2：根据两点的位置，进一步比较-2a和-2b的大小？

    引问3：乘以-2之后，不等式的符号是否发生了改变？

    通过上述的数轴验证，学生可以直观地认识到同时加上或乘以一个负数后不等式的符号是否发生改变，从而对不等式的性质有了深刻的认识. 这样做的优势在于证明过程直观简洁，知识关联性强，通过探究的方式可有效提升学生的能力.

    设计环节（四）——语言转换，素养提升

    数学语言是一种较为特殊的语言，不仅可以简洁地表达数学的性质定理，还具有极强的逻辑性，因此在教学不等式性质时有必要通过文字语言和数学语言的转换来增强学生对性质的认识，提升学生的语言表达能力.

    教学中需要让学生关注其中的数学符号，以及对应的语言描述，引导学生自主完成语言转换，建立数学语言与文字语言的对应关系，另外还需思考用数学语言描述性质具有哪些优点.

    设计环节（五）——性质应用，解决问题

    “性质应用”是性质学习的意义所在，在该阶段需要设计多样的问题，帮助学生巩固性质，掌握应用性质解决问题的方法. 而在设计问题时除了需要考虑全面性外，还需要考虑所设问题的多样性，确保代数类问题与实际问题相结合，提升学生思维的宽度和维度.

    问题1：用不等式的基本性质，求解下列不等式.

    （1）x-5>22;（2）x>50;

    （3）3x

    问题2：图5所示是某长方形容器，已知容器长5 cm、宽3 cm、高10 cm，若原容器内有水高3 cm，现先向其中注水，用V表示新注入水的体积，试写出V的取值范围.

    

    关于教学设计的反思

    1. 整合内容，树立主线

    本节内容是关于不等式的性质教学设计，按照“情景引入—类比探究—语言强化—拓展应用”的主线进行了内容编排. 上述主线的设计是基于对《课程标准》的解读和教材内容的整合，既关注学生对性质的探究体验，又注重学生的核心素养提升. 整个教学环節编排合理有序，逻辑严密，具有良好的教学效果. 因此，在设计教学时，需要教师深入解读教材，把握教学重难点，采用合理的方式完成教学引入、环节过渡和能力提升. 同时考虑“知识源于生活，服务于生活”的数学理念，促进学生知识和能力的双重提升.

    2. 类比探究，思维提升

    关注学生的知识水平和思维发展是现代教学的基本要求，因此在数学教学设计中需要以学生现有的发展水平为基础，采用合理的方式结合旧知，帮助学生完成新知的学习. 以本节“不等式的性质”的教学为例，考虑到学生已掌握等式的性质和数轴等知识，在教学时可充分把握知识联系性，通过类比探究、直观呈现的方式来引导学生归纳性质，验证结论. 整个过程以知识探究为主体，以学生的“最近发展区”为基础，帮助学生完成新知的探究，这样的教学方式不仅可以让学生体会到知识间的关联，还有助于学生思辨思维的发展，为学生核心素养的提升提供高效的平台.