基于标准,关注本质,培养素养
张雪
[摘 ?要] 在平行四边形的性质及判别条件的探究中,文章从关注平行四边形的本质出发,探讨如何增强学生的自主发现、主动探究的能力,培養学生构造数学模型等数学核心素养,提升教学的精神和价值追求.
[关键词] 标准;本质;素养;平行四边形教学
数学是一种“思维体操”,“生长数学”理念下的思维必然主张是指教师根据数学学习的具体内容,结合学生的思维发展规律,在数学知识的结构中,构建合适的思维场景,让学生在这个“思维场”中内生地、自然地产生必然的思维方向. 苏科版八年级下册§9.3《平行四边形》,在学习了《图形的旋转》《中心对称图形》的基础上展开学习. 这一部分分了三课时,主要学习任务是认识平行四边形,探究一个四边形是平行四边形的条件,利用平行四边形的性质和判别条件解决问题.
数学是数与形结合的学科,图形的学习应该注重概念本质的学习. 在概念本质的基础之上展开探究活动来研究它的性质等等.
教学片段1
问题1:平行四边形的定义是什么?
生:两组对边分别平行的四边形是平行四边形.
问题2:平行四边形由一个三角形通过怎样的图形运动得到?
生1:由三角形旋转得到.
生2:由三角形绕着三角形的一边中点旋转180度得到.
问题3:能得到平行四边形的哪些性质?
生1:两组对边平行,两组对角相等.
生2:对边相等.
生3:对角线连起来交点是中点.
生4:对角线互相平分.
问题4:如何验证得到的性质?
生1:全等.
生2:旋转的性质.
生3:平行四边形是中心对称图形,可以用中心对称的性质得到.
问题5:能将平行四边形的性质分类吗?
生1:边的关系:对边平行且相等.
生2:角的关系:对角相等,邻角互补.
生3:对角线互相平分.
生4:对称性:中心对称图形.
……
设计意图 第一课时的教学重难点是平行四边形的性质探究,在研学活动中,以问题串联整个教学活动,逐步引导学生去探究,在已有的知识结构和探究能力范围内学会自主探究,揭秘知识本质.在探究过程中注重归纳分类,构建探究图形性质的模式,为后续的矩形、菱形、正方形的探究学习提供了类比的基础和探究的模式.
教学片段2
问题1:满足什么条件的四边形是平行四边形?
生1:两组对边分别平行的四边形是平行四边形.
生2:一组对边平行且相等的四边形是平行四边形.
生3:对角线互相平分的四边形是平行四边形.
设计意图 引出本节课的探究主题,学生们预习的成果展示.这三个条件是书上给出的判别条件.下面将引导学生去探究其他的条件.
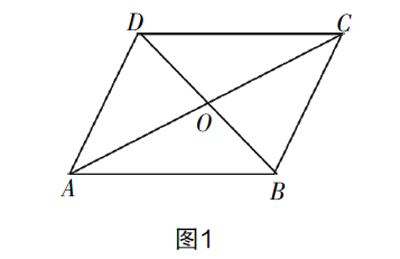
问题2:如图1,四边形ABCD中,①AB=CD,②AD=CB,③AB∥CD,④AD∥CB,⑤∠BAD=∠DCB,⑥∠ADC=∠CBA,⑦OA=OC,⑧OB=OD.
思考1:你能从中选择2组条件使得四边形是平行四边形吗?
生1:③④,由定义可以得知四边形为平行四边形.
生2:①②,由全等可以得知∠DAC=∠BCA,∠DCA=∠BAC,可以得到③④,由定义得到平行四边形.
生3:①③或②④,由全等也能得到条件③④,得到平行四边形.
生4:⑦⑧,由全等得到条件①②或③④或①③或②④,由此得平行四边形.
思考2:除了以上书本中给出的判定定理外,还有其他的组合是可以用来判别四边形是平行四边形的吗?
生1:①④,即四边形中有一组对边相等,另一组对边平行.
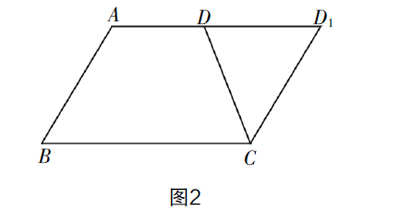
问:这样的四边形是平行四边形吗?如果不是,请举反例.
生2:等腰梯形,如图2.
生3:①⑤,即四边形中一组对边相等,一组对角相等.
师生探究:反例图.
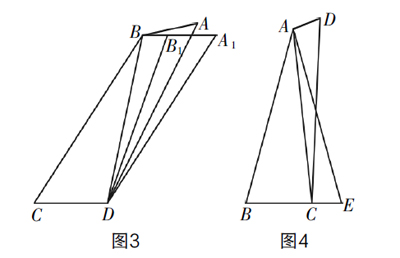
图3中,平行四边形A1BCD,DB=DB1,DA=DA1,∠BDA=∠B1DA1,则△ABD≌△A1B1D,则∠A=∠A1,AD=A1D.由平行四边形知:BC=DA1,∠C=∠A1,则BC=DA,∠C=∠A,而四边形ABCD不是平行四边形.
图4中,等腰三角形ABE,C是BE上异于中点的任意一点,△ACD≌△EAC,则∠B=∠E=∠D,AB=AE=CD,即AB=CD,∠B=∠D,而四边形ABCD不是平行四边形.
生4:①⑦,即四边形中一组对边相等,一条对角线被另一条对角线平分.
师生探究:反例图.
如图5,平行四边形AB1CD,AB=AB1,则OA=OC,AB=CD. 而四边形ABCD不是平行四边形.
生5:③⑤,即四边形中一组对边平行,一组对角相等.
师生探究:如图6,因为AB∥CD,所以∠A+∠D=180°. 因为∠A=∠C,所以∠C+∠D=180°,所以AD∥CB,所以四边形ABCD是平行四边形.
生6:③⑦,即四边形中一组对边平行,一条对角线被另一条对角线平分.
师生探究:如图7,因为AB∥CD,所以∠OCD=∠OAB,∠ODC=∠OBA. 又因为OA=OC,所以△AOB≌△COD. 所以AB=CD.所以四边形ABCD是平行四边形.
生7:⑤⑦,即四边形中一组对角相等,这组对角所夹的对角线被另一条对角线平分.
师生探究:反例图8:筝形.
如图8,∠BAD=∠DCB,OA=OC,而OB≠OD,四边形ABCD不是平行四边形.
设计意图 本节课探究平行四边形的判别条件,在原有的基础上,尊重学生预学的学习成果. 学生很容易找出课本中的4个判别条件.同时在本节课注重了在条件重组的背景下,自主探究,师生合作,由此掌握几何证明的一般方法:画反例图来证明假命题,几何说理来论证真命题. 在探究过程中,学生得到了12个命题,其中4个判定定理,4个真命题,4个假命题,并画出了反例图. 所有学习活动基于教学大纲标准,同时注重了对数学概念的本质的探究,促进数学核心素养的发展.
教学中注重了让学生固化类比源,激发最近联想,让学生“想得到”;构建思维链,营造逻辑连贯,让学生“想得妙”;编织体验包,聚焦一以贯之,让学生“想得透”. 在深入研究教学大纲、教学目标的基础上,设定的研学活动基于标准的同时,又尊重了学生. 探究活动中留足了思考空间,所有的研学活动围绕学生的最近发展区展开,学生能做的事绝不包办;注重培养学生的空间想象、几何说理等数学核心素养. 尤为重要的是要注重培养学生“悟”的能力.数学素养的培养是“悟”出来的,而不是“教”出来的,通过学生经历实践与思考的过程,不仅教给学生目前所需要的知识技能、方法技巧等应试能力,更培养学生未来发展所需要的数学思想、数学思考等数学素养,提升教学的精神和价值追求.

