例谈波利亚解题思想中的审题观
高建 李庆亮
[摘? 要] 对问题的表征是解决问题的开始,所以学生不够重视的审题环节恰恰是解题的重要一环,本文以波利亚解题思想为指导,介绍了解题的阶段、并以具体题目为例,对解题教学中审题环节的问题设置、方法指导等方面进行了探讨.
[关键词] 波利亚;审题;解题
依据《义务教育数学课程标准》的要求,学生要初步学会从数学的角度发现问题和提出问题,发现分析问题和解决问题的一些基本方法. 这既是义务教育阶段的要求,也是高中阶段发展学生“四能”的基础,而这些能力的提升都离不开解题教学. 但现在学校中的解题教学往往过于注重题目本身而忽视了能力的培养与发展,抑或有一些教师的解题教学不得方法,让学生的解题变为一种机械学习. 数学教育家波利亚指出“中学数学教学的首要任务就是要加强解题的训练”. 但这种“解题”不同于“题海战术”,他认为解题应该作为培养学生的数学才能和教会他们思考的一种手段和途径. 他在《怎样解题》中提供给人们一整套解题的思路与方法,不仅适用于数学问题,还对生活实际问题的解决提出了一定策略,对于中学阶段的数学解题教学具有指导意义.
波利亚的解题四阶段
波利亚在《怎样解题》中将解题分为了以下4个阶段:(1)理解题目,即明确题目中的未知量、已知数据、条件;(2)拟订方案,即找出题目中已知数据、条件以及未知量之间的联系,手中题目与相关概念之间的联系,该题目与之前做过的题目间的联系,并拟定一个求解计划;(3)执行方案,即实施之前拟定的计划,细化到每一个步骤,确保其过程严谨;(4)回顾,即对所求的解或证明的过程进行检验,对解题的思路与方法进行总结. 审题是解题的第一环节,若不能对题目形成正确的表征,解题也就无从谈起. 而在教学实践中可以发现,学生审题环节也存在着一些问题,所以本文将对审题环节进一步深入探讨.
理解题目
学生解题能力不足,除了知识点的整体把握不够之外,也与他们思考问题的方式有关,他们不知道怎样审题、怎样思考,而课堂教学或考试中往往有时间限制,这也就导致了一些学生还没有看清题目、理清条件就急于解题,若长此以往,这些学生或是长期做错而丧失对数学的兴趣,或是将错题归咎于马虎,或是偷证漏证而不自知,不论哪种结果都不利于学生的发展. 所以,教师在教学每一道题的解题过程时,更重要的是教学生解题的普遍思路与方法,教学生如何克服障碍,让学生看到教师解题时每一个想法的来源,这些就要从审题教学开始.
因“审题”而造成的问题是最可惜的,却也是最常见的. 中学生处于青少年时期本就不够沉稳,容易受心情、喜好等因素影响,遇到自己不感兴趣的题目就不愿意多做思考. 所以教师更应在题目的选择上下足功夫,既要选出有代表性的题目,也要保证题目的难度符合学生的最近发展区,还要考虑到习题与学生生活之间的联系,不能给学生一种“数学题与生活无关,不会做数学题只影响分数,不影响生活”的印象,同时在题量的控制上不能陷入“题海战术”. 为了达到以上要求,需要教师进入题海之中,对题目进行筛选,同时也需要教师之间互相交流,针对不同的学情筛选出不同层次、不同侧重点、不同表述的题目.
解题案例
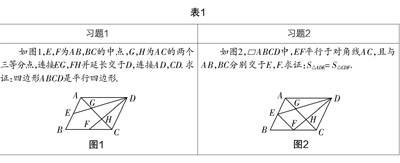
案例中(如表1)的两道题目在图形上看十分相似,且都是八年级下“平行四边形”一章的题目,但考点截然不同. 第1题中有明确给出“中点”字样的提示,结合当时刚学过的中位线的概念及性质,很容易联想到连接EF,虽然这样的思路无法解决这一题目,但由三角形两边中点,想到构造中位线确实是一种正常的思路. 而第2题中,E,F可能在AB,BC上的任意位置,只要满足EF与AC的平行关系即可,如果出题人将E,F的位置分别标在AB,BC的中点附近,学生便很容易将其与第一题混淆. 这种混淆究其根本在于学生并没有抓住图形的本质属性(即第2题中的几对平行关系),学生误将题目中的非本质属性(E,F的位置)当作图形的本质属性,从而陷入误区. 此时,由于一部分学生是审题导致的解题失败,教师若直接将两道题目的解法写在黑板上讲给学生,将不会有太大的效果. 这就要求教师从审题开始讲起,通过一系列的问题设置,教学生如何把握题目中数学对象的本质属性,剔除非本质属性的影响,从审题中获得思路.
问题设置
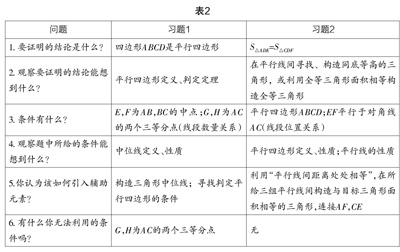
上述案例中,两题的考点截然不同,第一题更倾向平行四边形判定定理及中位线定义与性质的考核,第二题却考核了平行四边形的性质定理以及“平行线间距离处处相等”在有关面积问题中的应用. 教师在对图形或条件相近的习题讲解时更应按部就班,引导学生摒除前后习题之间的影响,从审题开始,先不断追问学生:未知量是什么?已知数据是什么?条件是什么?条件是否充分?如果不充分可以做怎样的补充?条件是否有剩余?不用多余的条件如何证明?在教师的不断追问下(如表2),学生潜移默化地就会养成做题之前先问自己这些问题的习惯.
在这样的引导之下,学生就可以清晰地看到两个题目的异同,从而对两个题目形成正确的表征,明确题目想要重点考查的知识点,也可以获得解题的思路,进而为拟定相应的解题方案做好了准备. 审题环节上的方法指导要围绕以下几点进行:①理解条件含义,并进行数学表征;②理解结论含义,并进行数学表征;③理清条件与结论之间的联系,这是审题环节进行设问的最终目的. 所以培养学生的审题能力,除讲解题目时的“设问”外,还应在课堂教学中对概念、原理进行多元表征(如:操作、日常语言、符号语言、图形等),以便学生又快又准地理解题目.
其他常用问题
教师对学生理解题意的引导应以问题作为提示,但绝不仅限于上述问题,还可以用如下问题对学生进行引导:对于这道题,我们所要求的是什么?该怎么用数学符号表示呢?现在我们知道了什么?该怎么用数学语言表示已知条件呢?对于目标问题,已知条件够用吗?如果不够,又该怎么办呢?如果已知条件多余呢?给出的条件相互矛盾吗?能不能把题目中的元素在图形上直观地表示出来呢……具体的问题设置还应分析具体学情,学生审题的难点可能在于符号语言、文字语言、图形语言的转化,或在于对问题情境的数学抽象与表征等很多方面,这就要求教师把握学情,在学生平时做题的步骤书写、图形标注等体现审题过程的细微之处加以观察,并根据其中的不足之处,在教学时合理设置问题.
现在仍有很多学生能听懂知识点,但在解题时却困难重重,其中很大一部分原因来自审题环节. 解题活动要培养的是学生的一种解决问题的思维方式,这种思维方式又无法直接告诉学生,教師要在平时的解题教学中,让学生“看到”自己的解题过程. 而审题又是解题活动的开端,是“四能”中“发现问题”的关键阶段,更应引起重视. 让学生知道教师是如何审题的,理解了题目也就为顺利解题做好了充分的准备,增加了学生自己完成解题的可能性,从而让学生体验到解题成功时的成就感,在解题的成就感中找到对数学的热爱.

